Structured Sparse Subspace Clustering: A Joint Affinity Learning and Subspace Clustering Framework

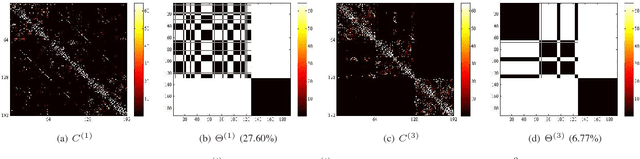
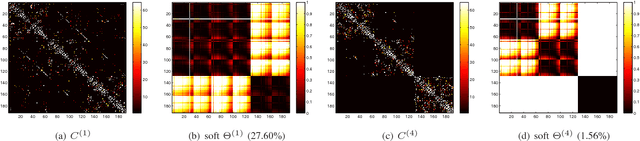
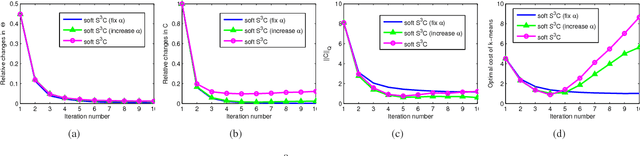
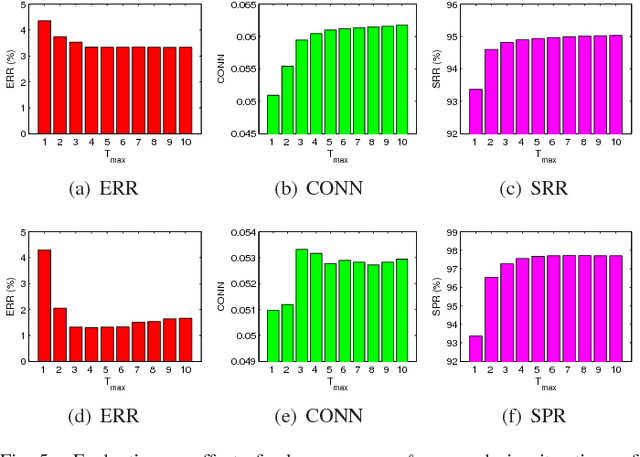
Subspace clustering refers to the problem of segmenting data drawn from a union of subspaces. State-of-the-art approaches for solving this problem follow a two-stage approach. In the first step, an affinity matrix is learned from the data using sparse or low-rank minimization techniques. In the second step, the segmentation is found by applying spectral clustering to this affinity. While this approach has led to state-of-the-art results in many applications, it is sub-optimal because it does not exploit the fact that the affinity and the segmentation depend on each other. In this paper, we propose a joint optimization framework --- Structured Sparse Subspace Clustering (S$^3$C) --- for learning both the affinity and the segmentation. The proposed S$^3$C framework is based on expressing each data point as a structured sparse linear combination of all other data points, where the structure is induced by a norm that depends on the unknown segmentation. Moreover, we extend the proposed S$^3$C framework into Constrained Structured Sparse Subspace Clustering (CS$^3$C) in which available partial side-information is incorporated into the stage of learning the affinity. We show that both the structured sparse representation and the segmentation can be found via a combination of an alternating direction method of multipliers with spectral clustering. Experiments on a synthetic data set, the Extended Yale B data set, the Hopkins 155 motion segmentation database, and three cancer data sets demonstrate the effectiveness of our approach.

Oracle Based Active Set Algorithm for Scalable Elastic Net Subspace Clustering

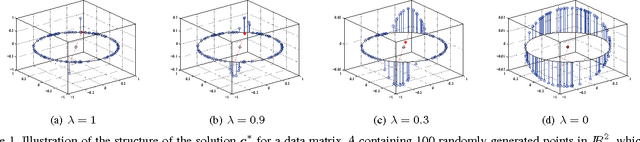
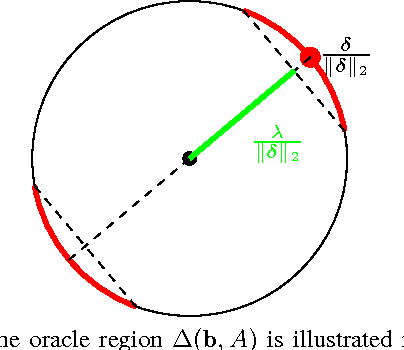
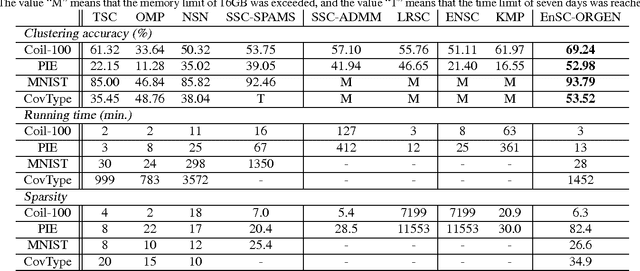
State-of-the-art subspace clustering methods are based on expressing each data point as a linear combination of other data points while regularizing the matrix of coefficients with $\ell_1$, $\ell_2$ or nuclear norms. $\ell_1$ regularization is guaranteed to give a subspace-preserving affinity (i.e., there are no connections between points from different subspaces) under broad theoretical conditions, but the clusters may not be connected. $\ell_2$ and nuclear norm regularization often improve connectivity, but give a subspace-preserving affinity only for independent subspaces. Mixed $\ell_1$, $\ell_2$ and nuclear norm regularizations offer a balance between the subspace-preserving and connectedness properties, but this comes at the cost of increased computational complexity. This paper studies the geometry of the elastic net regularizer (a mixture of the $\ell_1$ and $\ell_2$ norms) and uses it to derive a provably correct and scalable active set method for finding the optimal coefficients. Our geometric analysis also provides a theoretical justification and a geometric interpretation for the balance between the connectedness (due to $\ell_2$ regularization) and subspace-preserving (due to $\ell_1$ regularization) properties for elastic net subspace clustering. Our experiments show that the proposed active set method not only achieves state-of-the-art clustering performance, but also efficiently handles large-scale datasets.

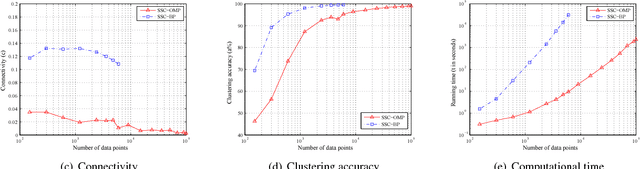
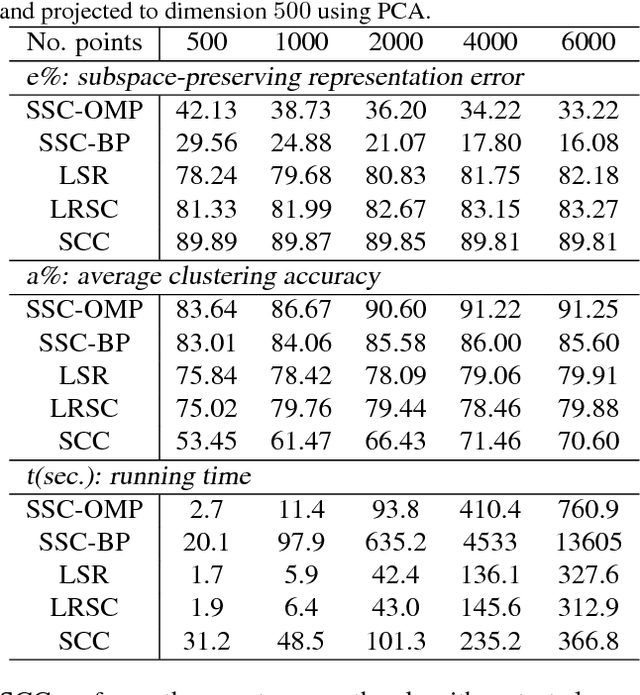
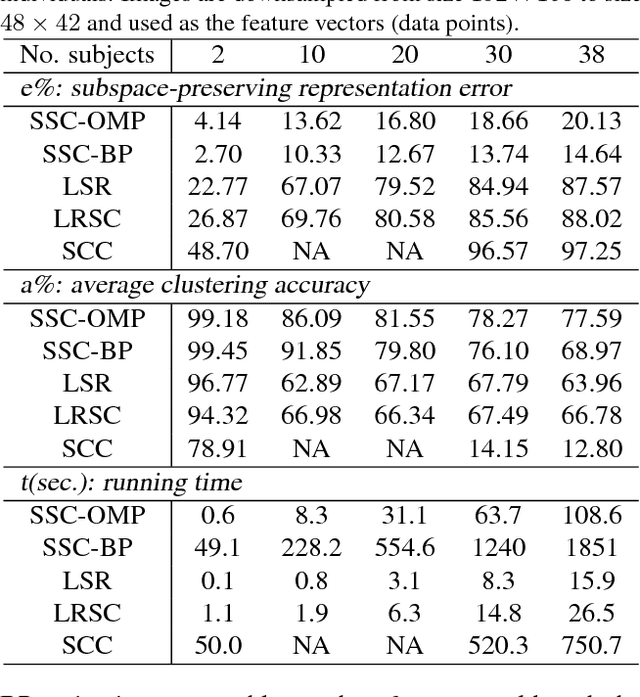
Scalable Sparse Subspace Clustering by Orthogonal Matching Pursuit

Subspace clustering methods based on $\ell_1$, $\ell_2$ or nuclear norm regularization have become very popular due to their simplicity, theoretical guarantees and empirical success. However, the choice of the regularizer can greatly impact both theory and practice. For instance, $\ell_1$ regularization is guaranteed to give a subspace-preserving affinity (i.e., there are no connections between points from different subspaces) under broad conditions (e.g., arbitrary subspaces and corrupted data). However, it requires solving a large scale convex optimization problem. On the other hand, $\ell_2$ and nuclear norm regularization provide efficient closed form solutions, but require very strong assumptions to guarantee a subspace-preserving affinity, e.g., independent subspaces and uncorrupted data. In this paper we study a subspace clustering method based on orthogonal matching pursuit. We show that the method is both computationally efficient and guaranteed to give a subspace-preserving affinity under broad conditions. Experiments on synthetic data verify our theoretical analysis, and applications in handwritten digit and face clustering show that our approach achieves the best trade off between accuracy and efficiency.