Linguistic and Argument Diversity in Synthetic Data for Function-Calling Agents

The construction of function calling agents has emerged as a promising avenue for extending model capabilities. A major challenge for this task is obtaining high quality diverse data for training. Prior work emphasizes diversity in functions, invocation patterns, and interaction turns, yet linguistic diversity of requests and coverage of arguments (e.g., \texttt{city\_name}, \texttt{stock\_ticker}) remain underexplored. We propose a method that generates synthetic datasets via optimizing general-purpose diversity metrics across both queries and arguments, without relying on hand-crafted rules or taxonomies, making it robust to different usecases. We demonstrate the effectiveness of our technique via both intrinsic and extrinsic testing, comparing it to SoTA data generation methods. We show a superiority over baselines in terms of diversity, while keeping comparable correctness. Additionally, when used as a training set, the model resulting from our dataset exhibits superior performance compared to analogous models based on the baseline data generation methods in out-of-distribution performance. In particular, we achieve an $7.4\%$ increase in accuracy on the BFCL benchmark compared to similar counterparts.

The Cross-Lingual Cost: Retrieval Biases in RAG over Arabic-English Corpora

Cross-lingual retrieval-augmented generation (RAG) is a critical capability for retrieving and generating answers across languages. Prior work in this context has mostly focused on generation and relied on benchmarks derived from open-domain sources, most notably Wikipedia. In such settings, retrieval challenges often remain hidden due to language imbalances, overlap with pretraining data, and memorized content. To address this gap, we study Arabic-English RAG in a domain-specific setting using benchmarks derived from real-world corporate datasets. Our benchmarks include all combinations of languages for the user query and the supporting document, drawn independently and uniformly at random. This enables a systematic study of multilingual retrieval behavior. Our findings reveal that retrieval is a critical bottleneck in cross-lingual domain-specific scenarios, with significant performance drops occurring when the user query and supporting document languages differ. A key insight is that these failures stem primarily from the retriever's difficulty in ranking documents across languages. Finally, we propose a simple retrieval strategy that addresses this source of failure by enforcing equal retrieval from both languages, resulting in substantial improvements in cross-lingual and overall performance. These results highlight meaningful opportunities for improving multilingual retrieval, particularly in practical, real-world RAG applications.

The Distracting Effect: Understanding Irrelevant Passages in RAG

A well-known issue with Retrieval Augmented Generation (RAG) is that retrieved passages that are irrelevant to the query sometimes distract the answer-generating LLM, causing it to provide an incorrect response. In this paper, we shed light on this core issue and formulate the distracting effect of a passage w.r.t. a query (and an LLM). We provide a quantifiable measure of the distracting effect of a passage and demonstrate its robustness across LLMs. Our research introduces novel methods for identifying and using hard distracting passages to improve RAG systems. By fine-tuning LLMs with these carefully selected distracting passages, we achieve up to a 7.5% increase in answering accuracy compared to counterparts fine-tuned on conventional RAG datasets. Our contribution is two-fold: first, we move beyond the simple binary classification of irrelevant passages as either completely unrelated vs. distracting, and second, we develop and analyze multiple methods for finding hard distracting passages. To our knowledge, no other research has provided such a comprehensive framework for identifying and utilizing hard distracting passages.

Distributed Sparse Linear Regression with Sublinear Communication

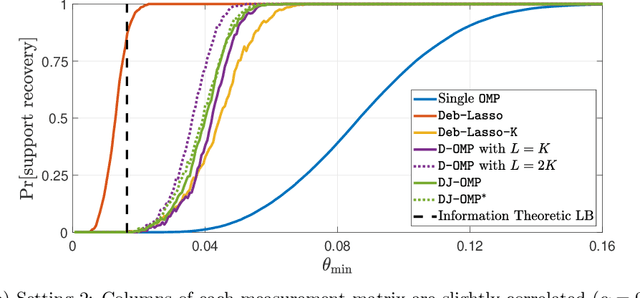
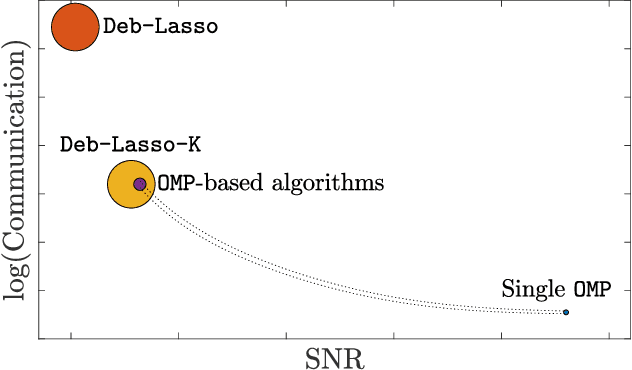
We study the problem of high-dimensional sparse linear regression in a distributed setting under both computational and communication constraints. Specifically, we consider a star topology network whereby several machines are connected to a fusion center, with whom they can exchange relatively short messages. Each machine holds noisy samples from a linear regression model with the same unknown sparse $d$-dimensional vector of regression coefficients $\theta$. The goal of the fusion center is to estimate the vector $\theta$ and its support using few computations and limited communication at each machine. In this work, we consider distributed algorithms based on Orthogonal Matching Pursuit (OMP) and theoretically study their ability to exactly recover the support of $\theta$. We prove that under certain conditions, even at low signal-to-noise-ratios where individual machines are unable to detect the support of $\theta$, distributed-OMP methods correctly recover it with total communication sublinear in $d$. In addition, we present simulations that illustrate the performance of distributed OMP-based algorithms and show that they perform similarly to more sophisticated and computationally intensive methods, and in some cases even outperform them.

Sparse Normal Means Estimation with Sublinear Communication

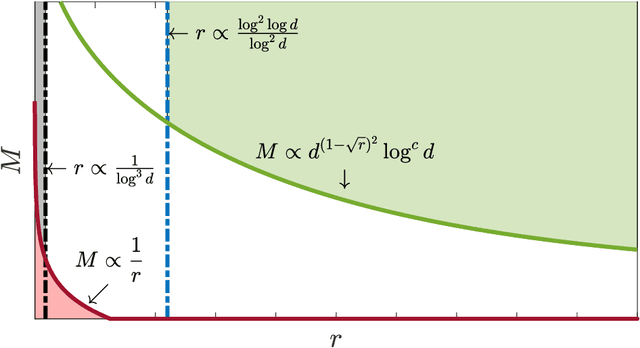
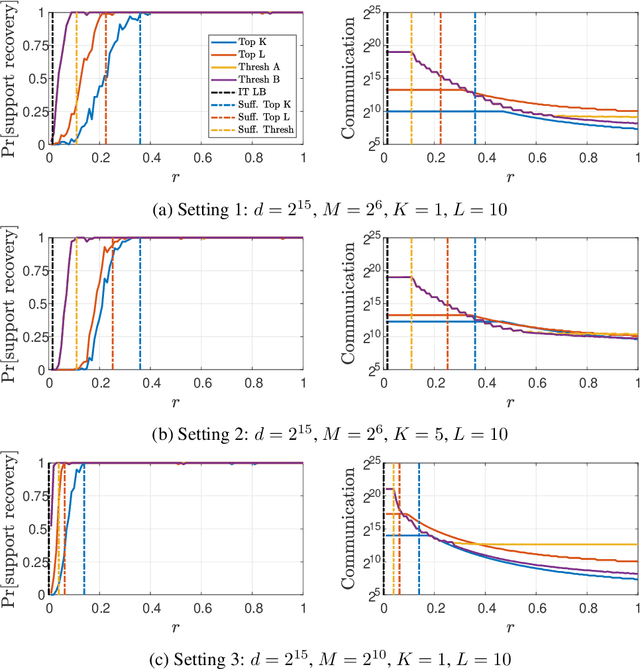
We consider the problem of sparse normal means estimation in a distributed setting with communication constraints. We assume there are $M$ machines, each holding a $d$-dimensional observation of a $K$-sparse vector $\mu$ corrupted by additive Gaussian noise. A central fusion machine is connected to the $M$ machines in a star topology, and its goal is to estimate the vector $\mu$ with a low communication budget. Previous works have shown that to achieve the centralized minimax rate for the $\ell_2$ risk, the total communication must be high - at least linear in the dimension $d$. This phenomenon occurs, however, at very weak signals. We show that once the signal-to-noise ratio (SNR) is slightly higher, the support of $\mu$ can be correctly recovered with much less communication. Specifically, we present two algorithms for the distributed sparse normal means problem, and prove that above a certain SNR threshold, with high probability, they recover the correct support with total communication that is sublinear in the dimension $d$. Furthermore, the communication decreases exponentially as a function of signal strength. If in addition $KM\ll d$, then with an additional round of sublinear communication, our algorithms achieve the centralized rate for the $\ell_2$ risk. Finally, we present simulations that illustrate the performance of our algorithms in different parameter regimes.