Hierarchical Forecast Reconciliation on Networks: A Network Flow Optimization Formulation

Hierarchical forecasting with reconciliation requires forecasting values of a hierarchy (e.g.~customer demand in a state and district), such that forecast values are linked (e.g.~ district forecasts should add up to the state forecast). Basic forecasting provides no guarantee for these desired structural relationships. Reconciliation addresses this problem, which is crucial for organizations requiring coherent predictions across multiple aggregation levels. Current methods like minimum trace (MinT) are mostly limited to tree structures and are computationally expensive. We introduce FlowRec, which reformulates hierarchical forecast reconciliation as a network flow optimization, enabling forecasting on generalized network structures. While reconciliation under the $\ell_0$ norm is NP-hard, we prove polynomial-time solvability for all $\ell_{p > 0}$ norms and , for any strictly convex and continuously differentiable loss function. For sparse networks, FlowRec achieves $O(n^2\log n)$ complexity, significantly improving upon MinT's $O(n^3)$. Furthermore, we prove that FlowRec extends MinT to handle general networks, replacing MinT's error-covariance estimation step with direct network structural information. A key novelty of our approach is its handling of dynamic scenarios: while traditional methods recompute both base forecasts and reconciliation, FlowRec provides efficient localised updates with optimality guarantees. Monotonicity ensures that when forecasts improve incrementally, the initial reconciliation remains optimal. We also establish efficient, error-bounded approximate reconciliation, enabling fast updates in time-critical applications. Experiments on both simulated and real benchmarks demonstrate that FlowRec improves accuracy, runtime by 3-40x and memory usage by 5-7x. These results establish FlowRec as a powerful tool for large-scale hierarchical forecasting applications.

Scalable Bayesian Network Structure Learning with Splines

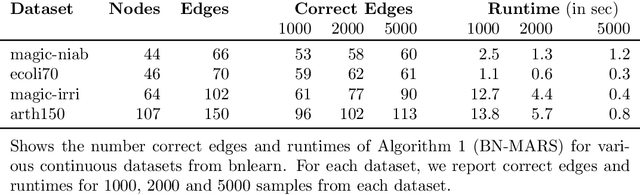
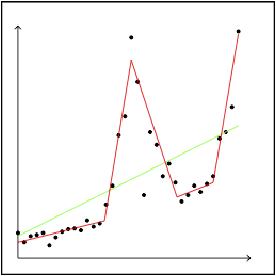
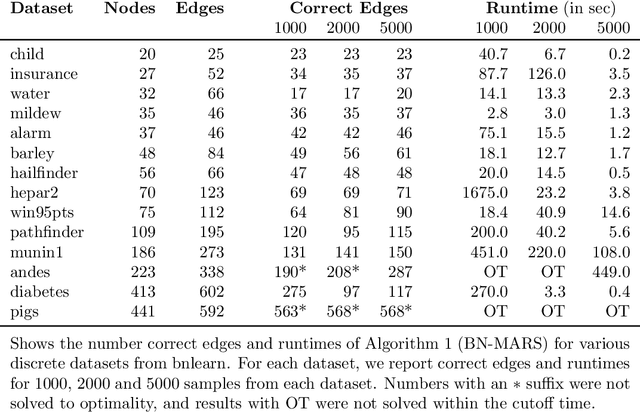
A Bayesian Network (BN) is a probabilistic graphical model consisting of a directed acyclic graph (DAG), where each node is a random variable represented as a function of its parents. We present a novel approach capable of learning the global DAG structure of a BN and modelling linear and non-linear local relationships between variables. We achieve this by a combination of feature selection to reduce the search space for local relationships, and extending the widely used score-and-search approach to support modelling relationships between variables as Multivariate Adaptive Regression Splines (MARS). MARS are polynomial regression models represented as piecewise spline functions - this lets us model non-linear relationships without the risk of overfitting that a single polynomial regression model would bring. The combination allows us to learn relationships in all bnlearn benchmark instances within minutes and enables us to scale to networks of over a thousand nodes

A Score-and-Search Approach to Learning Bayesian Networks with Noisy-OR Relations

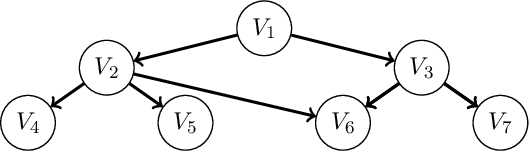
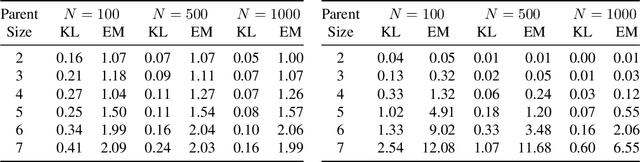
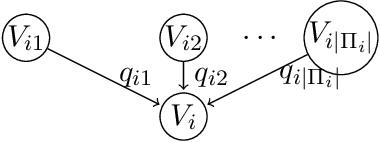
A Bayesian network is a probabilistic graphical model that consists of a directed acyclic graph (DAG), where each node is a random variable and attached to each node is a conditional probability distribution (CPD). A Bayesian network can be learned from data using the well-known score-and-search approach, and within this approach a key consideration is how to simultaneously learn the global structure in the form of the underlying DAG and the local structure in the CPDs. Several useful forms of local structure have been identified in the literature but thus far the score-and-search approach has only been extended to handle local structure in form of context-specific independence. In this paper, we show how to extend the score-and-search approach to the important and widely useful case of noisy-OR relations. We provide an effective gradient descent algorithm to score a candidate noisy-OR using the widely used BIC score and we provide pruning rules that allow the search to successfully scale to medium sized networks. Our empirical results provide evidence for the success of our approach to learning Bayesian networks that incorporate noisy-OR relations.

Learning All Credible Bayesian Network Structures for Model Averaging

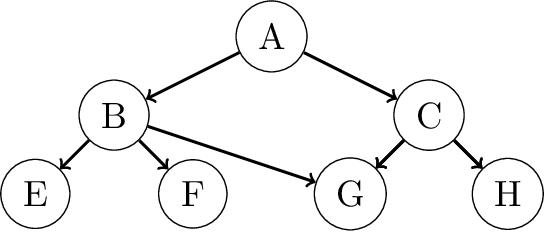
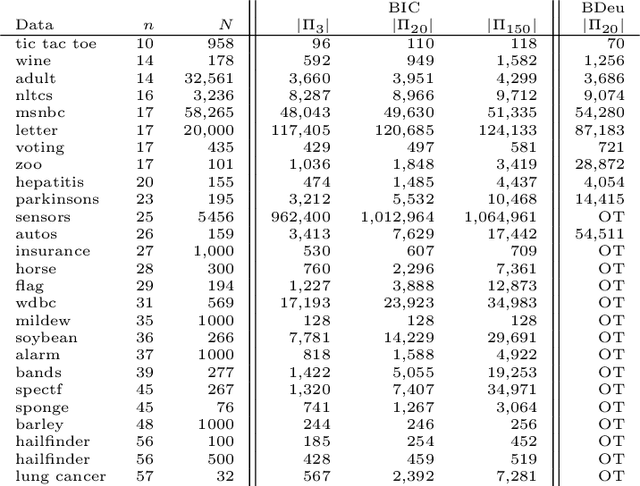
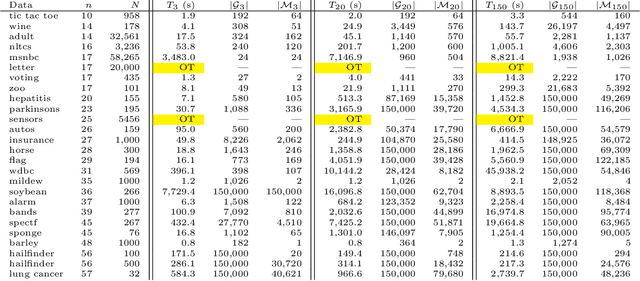
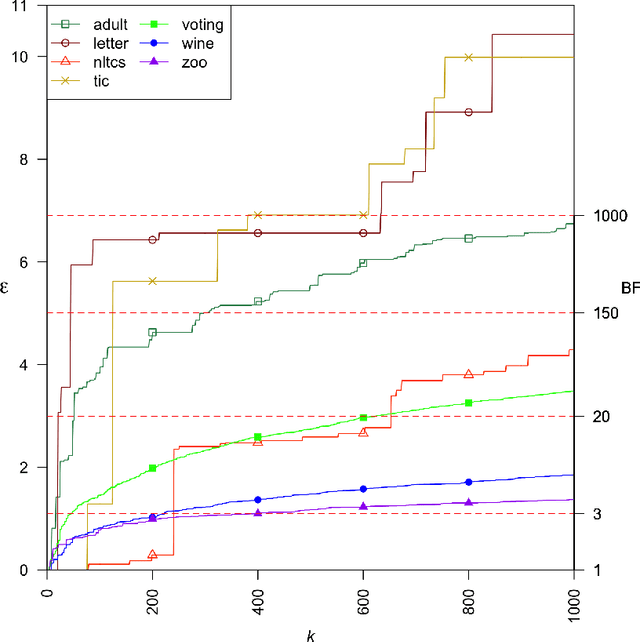
A Bayesian network is a widely used probabilistic graphical model with applications in knowledge discovery and prediction. Learning a Bayesian network (BN) from data can be cast as an optimization problem using the well-known score-and-search approach. However, selecting a single model (i.e., the best scoring BN) can be misleading or may not achieve the best possible accuracy. An alternative to committing to a single model is to perform some form of Bayesian or frequentist model averaging, where the space of possible BNs is sampled or enumerated in some fashion. Unfortunately, existing approaches for model averaging either severely restrict the structure of the Bayesian network or have only been shown to scale to networks with fewer than 30 random variables. In this paper, we propose a novel approach to model averaging inspired by performance guarantees in approximation algorithms. Our approach has two primary advantages. First, our approach only considers credible models in that they are optimal or near-optimal in score. Second, our approach is more efficient and scales to significantly larger Bayesian networks than existing approaches.

Finding All Bayesian Network Structures within a Factor of Optimal

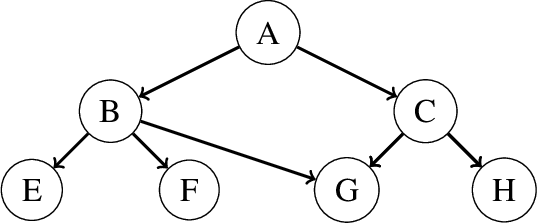
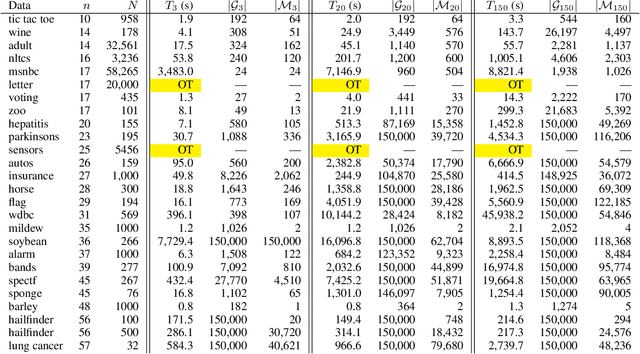
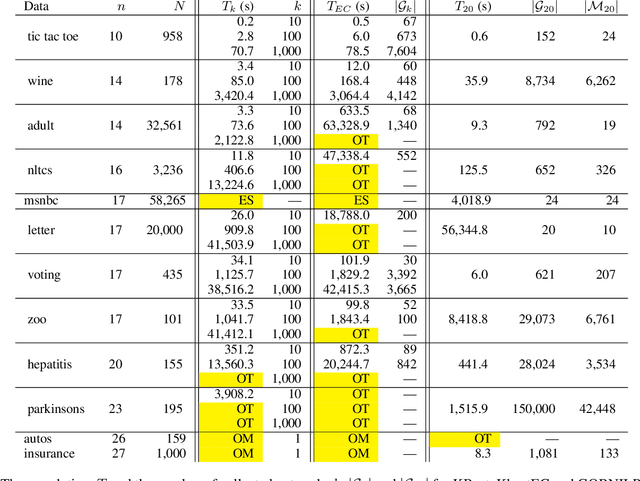
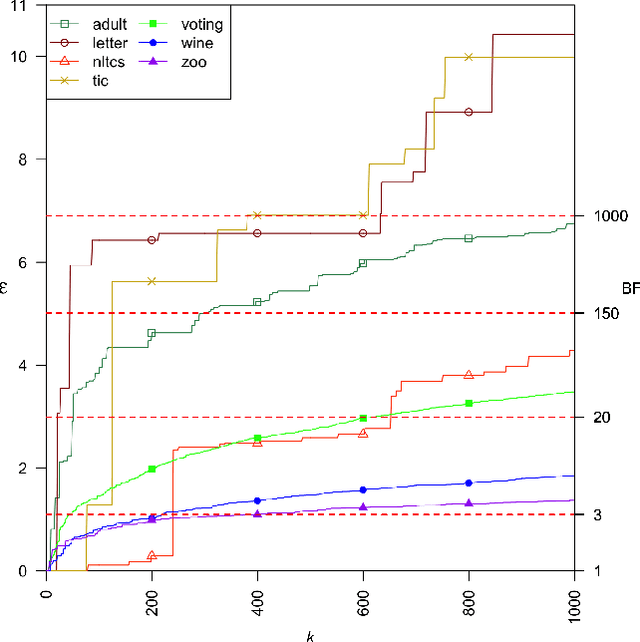
A Bayesian network is a widely used probabilistic graphical model with applications in knowledge discovery and prediction. Learning a Bayesian network (BN) from data can be cast as an optimization problem using the well-known score-and-search approach. However, selecting a single model (i.e., the best scoring BN) can be misleading or may not achieve the best possible accuracy. An alternative to committing to a single model is to perform some form of Bayesian or frequentist model averaging, where the space of possible BNs is sampled or enumerated in some fashion. Unfortunately, existing approaches for model averaging either severely restrict the structure of the Bayesian network or have only been shown to scale to networks with fewer than 30 random variables. In this paper, we propose a novel approach to model averaging inspired by performance guarantees in approximation algorithms. Our approach has two primary advantages. First, our approach only considers credible models in that they are optimal or near-optimal in score. Second, our approach is more efficient and scales to significantly larger Bayesian networks than existing approaches.