Chao Pan
Certified Graph Unlearning
Jun 18, 2022
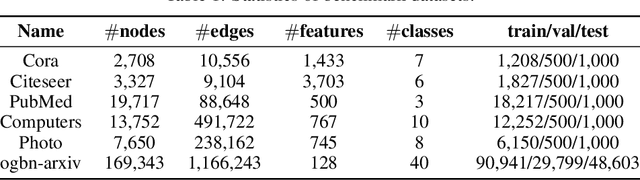

Abstract:Graph-structured data is ubiquitous in practice and often processed using graph neural networks (GNNs). With the adoption of recent laws ensuring the ``right to be forgotten'', the problem of graph data removal has become of significant importance. To address the problem, we introduce the first known framework for \emph{certified graph unlearning} of GNNs. In contrast to standard machine unlearning, new analytical and heuristic unlearning challenges arise when dealing with complex graph data. First, three different types of unlearning requests need to be considered, including node feature, edge and node unlearning. Second, to establish provable performance guarantees, one needs to address challenges associated with feature mixing during propagation. The underlying analysis is illustrated on the example of simple graph convolutions (SGC) and their generalized PageRank (GPR) extensions, thereby laying the theoretical foundation for certified unlearning of GNNs. Our empirical studies on six benchmark datasets demonstrate excellent performance-complexity trade-offs when compared to complete retraining methods and approaches that do not leverage graph information. For example, when unlearning $20\%$ of the nodes on the Cora dataset, our approach suffers only a $0.1\%$ loss in test accuracy while offering a $4$-fold speed-up compared to complete retraining. Our scheme also outperforms unlearning methods that do not leverage graph information with a $12\%$ increase in test accuracy for a comparable time complexity.
Provably Accurate and Scalable Linear Classifiers in Hyperbolic Spaces
Mar 11, 2022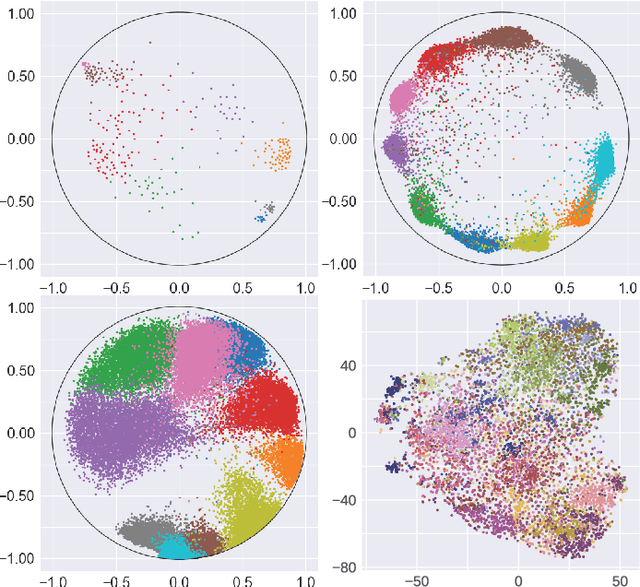
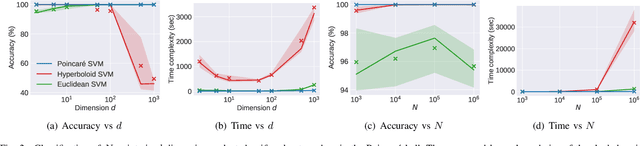
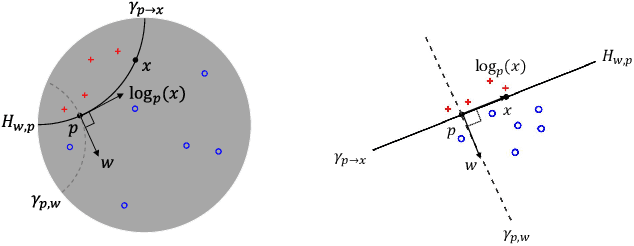
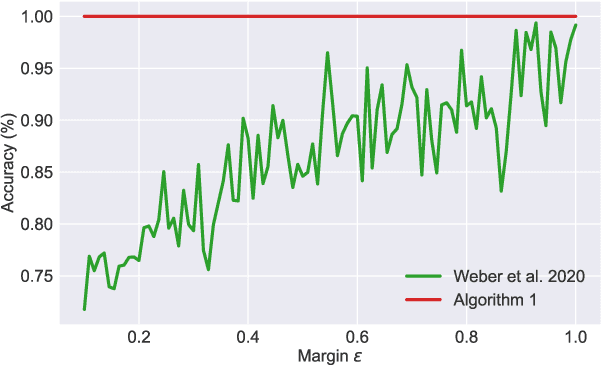
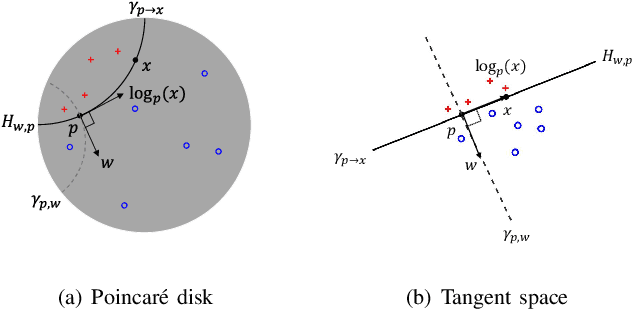
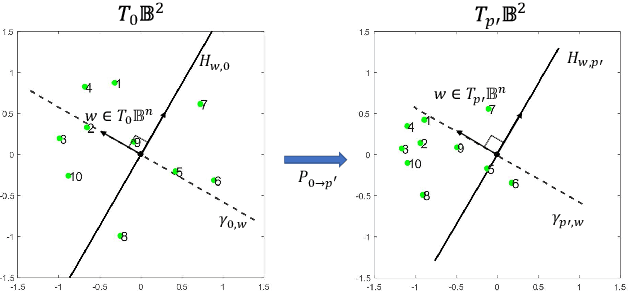
Abstract:Many high-dimensional practical data sets have hierarchical structures induced by graphs or time series. Such data sets are hard to process in Euclidean spaces and one often seeks low-dimensional embeddings in other space forms to perform the required learning tasks. For hierarchical data, the space of choice is a hyperbolic space because it guarantees low-distortion embeddings for tree-like structures. The geometry of hyperbolic spaces has properties not encountered in Euclidean spaces that pose challenges when trying to rigorously analyze algorithmic solutions. We propose a unified framework for learning scalable and simple hyperbolic linear classifiers with provable performance guarantees. The gist of our approach is to focus on Poincar\'e ball models and formulate the classification problems using tangent space formalisms. Our results include a new hyperbolic perceptron algorithm as well as an efficient and highly accurate convex optimization setup for hyperbolic support vector machine classifiers. Furthermore, we adapt our approach to accommodate second-order perceptrons, where data is preprocessed based on second-order information (correlation) to accelerate convergence, and strategic perceptrons, where potentially manipulated data arrives in an online manner and decisions are made sequentially. The excellent performance of the Poincar\'e second-order and strategic perceptrons shows that the proposed framework can be extended to general machine learning problems in hyperbolic spaces. Our experimental results, pertaining to synthetic, single-cell RNA-seq expression measurements, CIFAR10, Fashion-MNIST and mini-ImageNet, establish that all algorithms provably converge and have complexity comparable to those of their Euclidean counterparts. Accompanying codes can be found at: https://github.com/thupchnsky/PoincareLinearClassification.
Highly Scalable and Provably Accurate Classification in Poincare Balls
Sep 15, 2021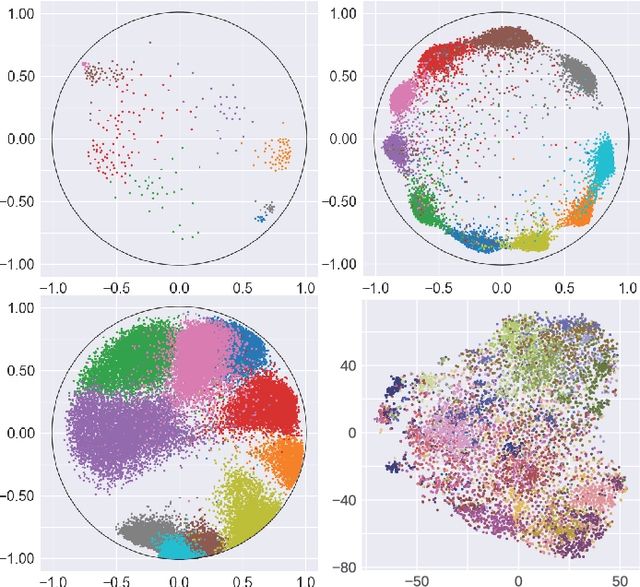
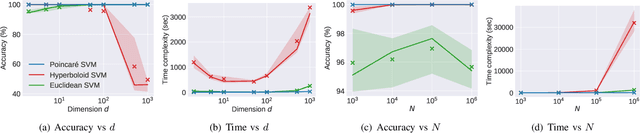
Abstract:Many high-dimensional and large-volume data sets of practical relevance have hierarchical structures induced by trees, graphs or time series. Such data sets are hard to process in Euclidean spaces and one often seeks low-dimensional embeddings in other space forms to perform required learning tasks. For hierarchical data, the space of choice is a hyperbolic space since it guarantees low-distortion embeddings for tree-like structures. Unfortunately, the geometry of hyperbolic spaces has properties not encountered in Euclidean spaces that pose challenges when trying to rigorously analyze algorithmic solutions. Here, for the first time, we establish a unified framework for learning scalable and simple hyperbolic linear classifiers with provable performance guarantees. The gist of our approach is to focus on Poincar\'e ball models and formulate the classification problems using tangent space formalisms. Our results include a new hyperbolic and second-order perceptron algorithm as well as an efficient and highly accurate convex optimization setup for hyperbolic support vector machine classifiers. All algorithms provably converge and are highly scalable as they have complexities comparable to those of their Euclidean counterparts. Their performance accuracies on synthetic data sets comprising millions of points, as well as on complex real-world data sets such as single-cell RNA-seq expression measurements, CIFAR10, Fashion-MNIST and mini-ImageNet.
You are AllSet: A Multiset Function Framework for Hypergraph Neural Networks
Jun 24, 2021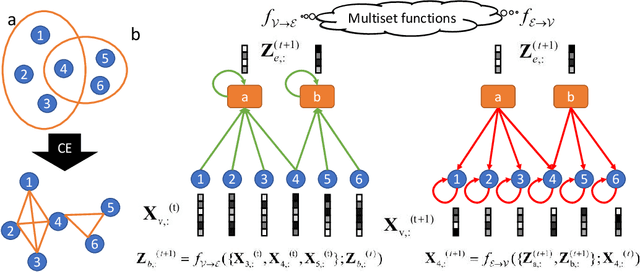
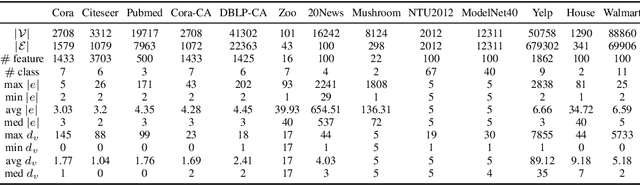
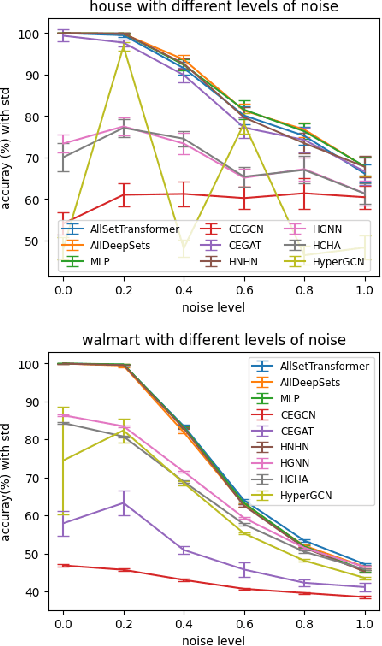
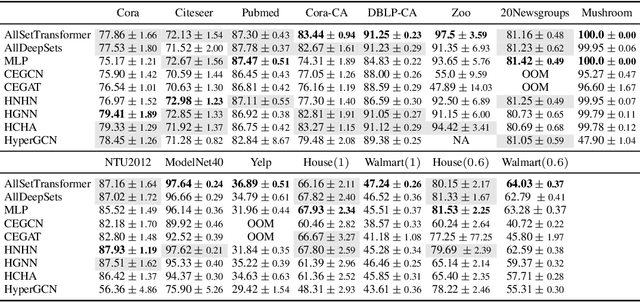
Abstract:Hypergraphs are used to model higher-order interactions amongst agents and there exist many practically relevant instances of hypergraph datasets. To enable efficient processing of hypergraph-structured data, several hypergraph neural network platforms have been proposed for learning hypergraph properties and structure, with a special focus on node classification. However, almost all existing methods use heuristic propagation rules and offer suboptimal performance on many datasets. We propose AllSet, a new hypergraph neural network paradigm that represents a highly general framework for (hyper)graph neural networks and for the first time implements hypergraph neural network layers as compositions of two multiset functions that can be efficiently learned for each task and each dataset. Furthermore, AllSet draws on new connections between hypergraph neural networks and recent advances in deep learning of multiset functions. In particular, the proposed architecture utilizes Deep Sets and Set Transformer architectures that allow for significant modeling flexibility and offer high expressive power. To evaluate the performance of AllSet, we conduct the most extensive experiments to date involving ten known benchmarking datasets and three newly curated datasets that represent significant challenges for hypergraph node classification. The results demonstrate that AllSet has the unique ability to consistently either match or outperform all other hypergraph neural networks across the tested datasets. Our implementation and dataset will be released upon acceptance.
Linear Classifiers in Mixed Constant Curvature Spaces
Feb 19, 2021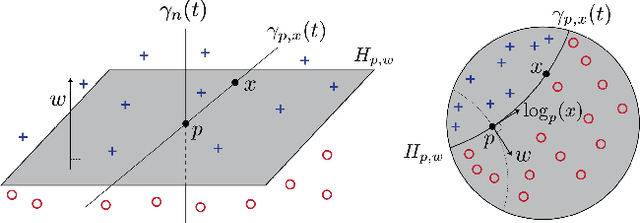
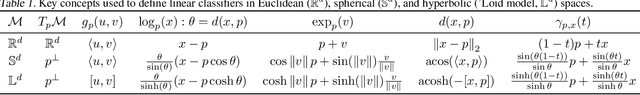
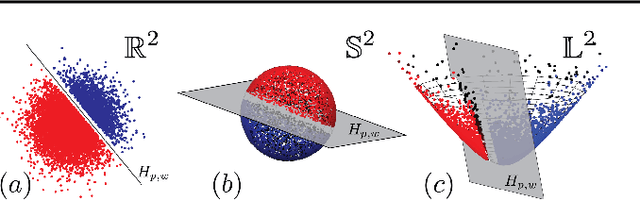
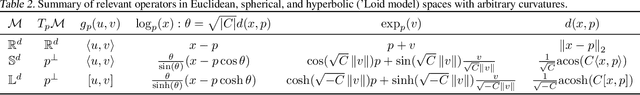
Abstract:Embedding methods for mixed-curvature spaces are powerful techniques for low-distortion and low-dimensional representation of complex data structures. Nevertheless, little is known regarding downstream learning and optimization in the embedding space. Here, we address for the first time the problem of linear classification in a product space form -- a mix of Euclidean, spherical, and hyperbolic spaces with different dimensions. First, we revisit the definition of a linear classifier on a Riemannian manifold by using geodesics and Riemannian metrics which generalize the notions of straight lines and inner products in vector spaces, respectively. Second, we prove that linear classifiers in $d$-dimensional constant curvature spaces can shatter exactly $d+1$ points: Hence, Euclidean, hyperbolic and spherical classifiers have the same expressive power. Third, we formalize linear classifiers in product space forms, describe a novel perceptron classification algorithm, and establish rigorous convergence results. We support our theoretical findings with simulation results on several datasets, including synthetic data, MNIST and Omniglot. Our results reveal that learning methods applied to small-dimensional embeddings in product space forms significantly outperform their algorithmic counterparts in Euclidean spaces.
Spatio-Temporal Graph Scattering Transform
Dec 10, 2020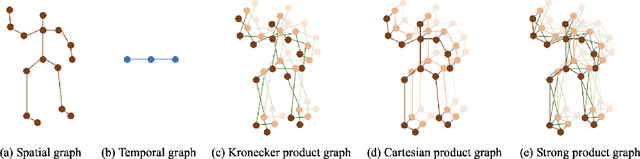
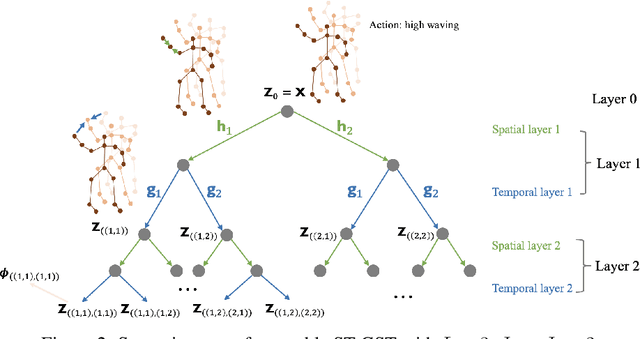

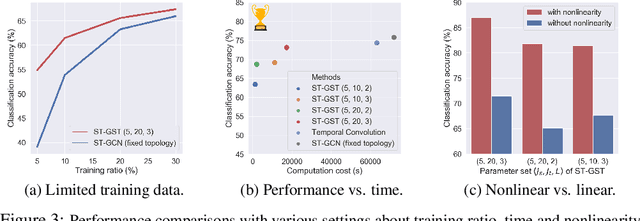
Abstract:Although spatio-temporal graph neural networks have achieved great empirical success in handling multiple correlated time series, they may be impractical in some real-world scenarios due to a lack of sufficient high-quality training data. Furthermore, spatio-temporal graph neural networks lack theoretical interpretation. To address these issues, we put forth a novel mathematically designed framework to analyze spatio-temporal data. Our proposed spatio-temporal graph scattering transform (ST-GST) extends traditional scattering transforms to the spatio-temporal domain. It performs iterative applications of spatio-temporal graph wavelets and nonlinear activation functions, which can be viewed as a forward pass of spatio-temporal graph convolutional networks without training. Since all the filter coefficients in ST-GST are mathematically designed, it is promising for the real-world scenarios with limited training data, and also allows for a theoretical analysis, which shows that the proposed ST-GST is stable to small perturbations of input signals and structures. Finally, our experiments show that i) ST-GST outperforms spatio-temporal graph convolutional networks by an increase of 35% in accuracy for MSR Action3D dataset; ii) it is better and computationally more efficient to design the transform based on separable spatio-temporal graphs than the joint ones; and iii) the nonlinearity in ST-GST is critical to empirical performance.
Image processing in DNA
Oct 22, 2019
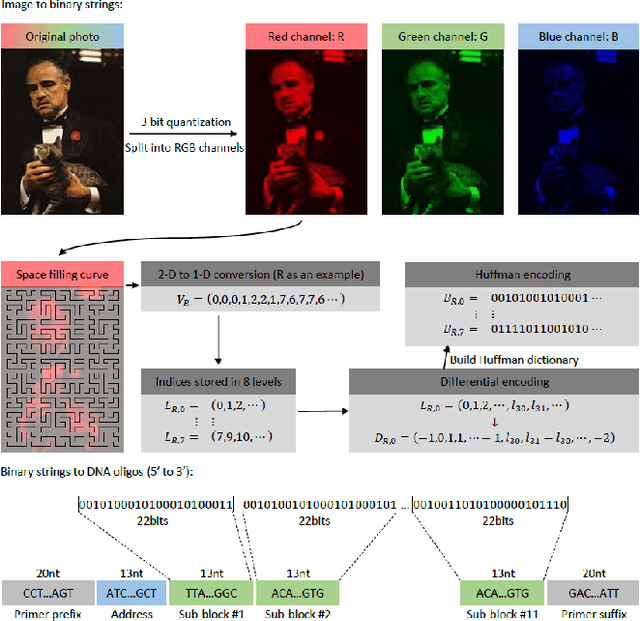


Abstract:The main obstacles for the practical deployment of DNA-based data storage platforms are the prohibitively high cost of synthetic DNA and the large number of errors introduced during synthesis. In particular, synthetic DNA products contain both individual oligo (fragment) symbol errors as well as missing DNA oligo errors, with rates that exceed those of modern storage systems by orders of magnitude. These errors can be corrected either through the use of a large number of redundant oligos or through cycles of writing, reading, and rewriting of information that eliminate the errors. Both approaches add to the overall storage cost and are hence undesirable. Here we propose the first method for storing quantized images in DNA that uses signal processing and machine learning techniques to deal with error and cost issues without resorting to the use of redundant oligos or rewriting. Our methods rely on decoupling the RGB channels of images, performing specialized quantization and compression on the individual color channels, and using new discoloration detection and image inpainting techniques. We demonstrate the performance of our approach experimentally on a collection of movie posters stored in DNA.
Query K-means Clustering and the Double Dixie Cup Problem
Jun 15, 2018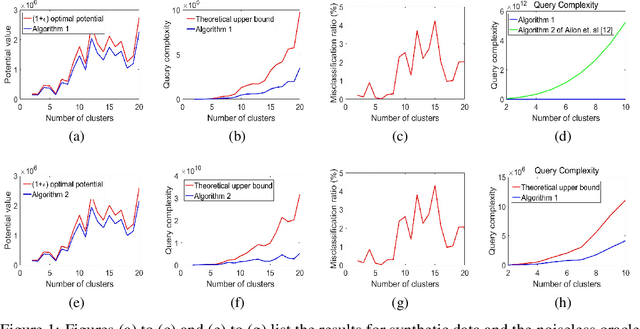
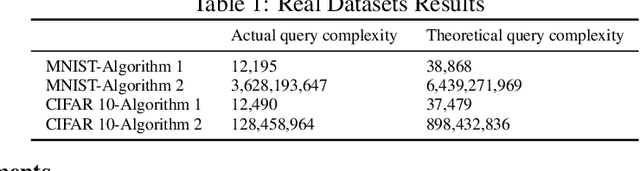
Abstract:We consider the problem of approximate $K$-means clustering with outliers and side information provided by same-cluster queries and possibly noisy answers. Our solution shows that, under some mild assumptions on the smallest cluster size, one can obtain an $(1+\epsilon)$-approximation for the optimal potential with probability at least $1-\delta$, where $\epsilon>0$ and $\delta\in(0,1)$, using an expected number of $O(\frac{K^3}{\epsilon \delta})$ noiseless same-cluster queries and comparison-based clustering of complexity $O(ndK + \frac{K^3}{\epsilon \delta})$, here, $n$ denotes the number of points and $d$ the dimension of space. Compared to a handful of other known approaches that perform importance sampling to account for small cluster sizes, the proposed query technique reduces the number of queries by a factor of roughly $O(\frac{K^6}{\epsilon^3})$, at the cost of possibly missing very small clusters. We extend this settings to the case where some queries to the oracle produce erroneous information, and where certain points, termed outliers, do not belong to any clusters. Our proof techniques differ from previous methods used for $K$-means clustering analysis, as they rely on estimating the sizes of the clusters and the number of points needed for accurate centroid estimation and subsequent nontrivial generalizations of the double Dixie cup problem. We illustrate the performance of the proposed algorithm both on synthetic and real datasets, including MNIST and CIFAR $10$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge