Breaking Fair Binary Classification with Optimal Flipping Attacks

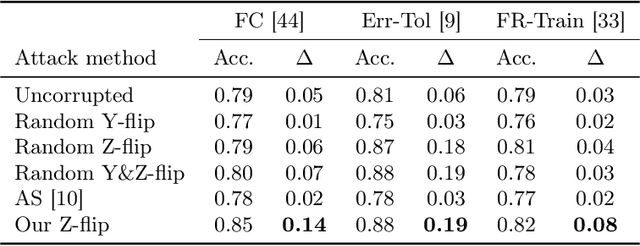
Minimizing risk with fairness constraints is one of the popular approaches to learning a fair classifier. Recent works showed that this approach yields an unfair classifier if the training set is corrupted. In this work, we study the minimum amount of data corruption required for a successful flipping attack. First, we find lower/upper bounds on this quantity and show that these bounds are tight when the target model is the unique unconstrained risk minimizer. Second, we propose a computationally efficient data poisoning attack algorithm that can compromise the performance of fair learning algorithms.

Discrete-valued Preference Estimation with Graph Side Information

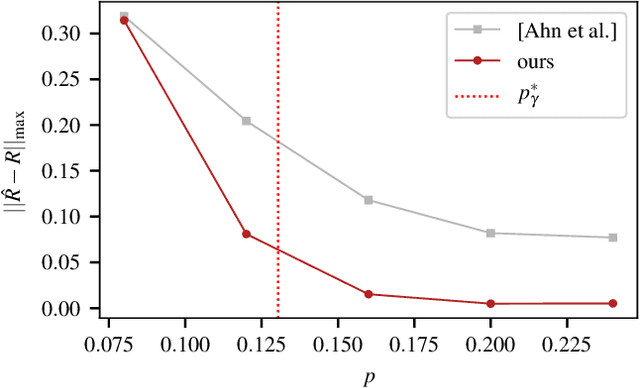
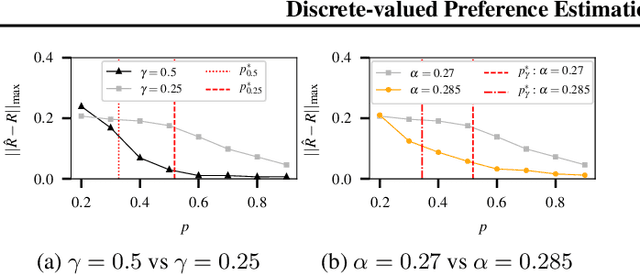
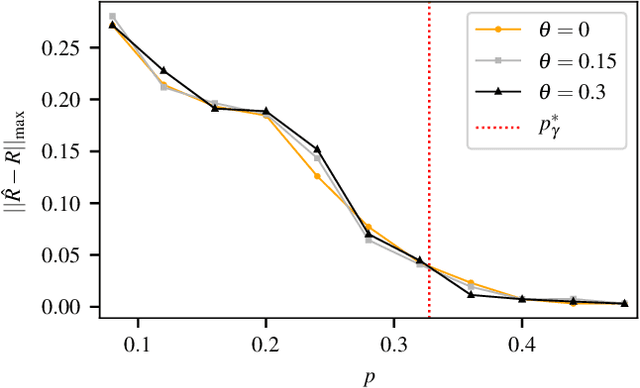
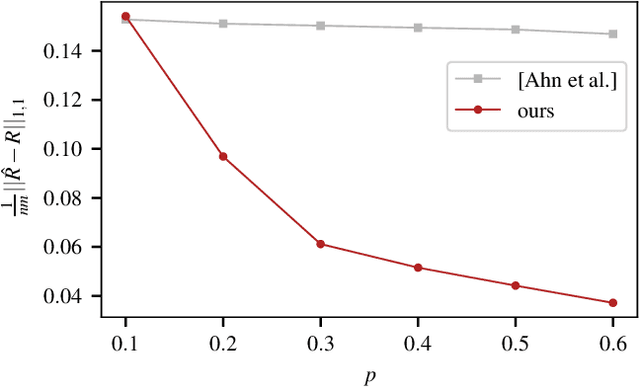
Incorporating graph side information into recommender systems has been widely used to better predict ratings, but relatively few works have focused on theoretical guarantees. Ahn et al. (2018) firstly characterized the optimal sample complexity in the presence of graph side information, but the results are limited due to strict, unrealistic assumptions made on the unknown preference matrix. In this work, we propose a new model in which the unknown preference matrix can have any discrete values, thereby relaxing the assumptions made in prior work. Under this new model, we fully characterize the optimal sample complexity and develop a computationally-efficient algorithm that matches the optimal sample complexity. We also show that our algorithm is robust to model errors, and it outperforms existing algorithms on both synthetic and real datasets.