Hypergraph Spectral Clustering in the Weighted Stochastic Block Model

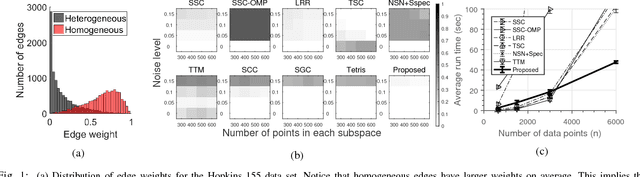
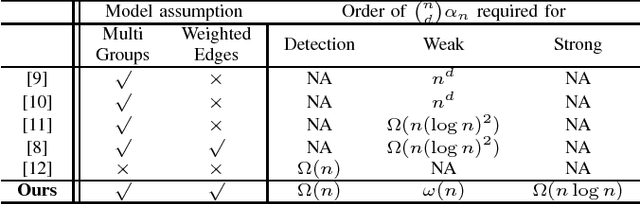
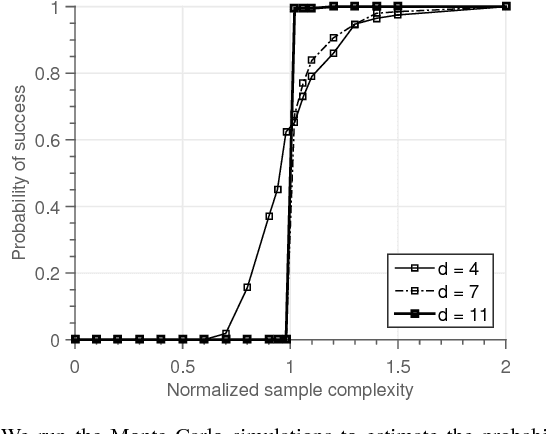
Spectral clustering is a celebrated algorithm that partitions objects based on pairwise similarity information. While this approach has been successfully applied to a variety of domains, it comes with limitations. The reason is that there are many other applications in which only \emph{multi}-way similarity measures are available. This motivates us to explore the multi-way measurement setting. In this work, we develop two algorithms intended for such setting: Hypergraph Spectral Clustering (HSC) and Hypergraph Spectral Clustering with Local Refinement (HSCLR). Our main contribution lies in performance analysis of the poly-time algorithms under a random hypergraph model, which we name the weighted stochastic block model, in which objects and multi-way measures are modeled as nodes and weights of hyperedges, respectively. Denoting by $n$ the number of nodes, our analysis reveals the following: (1) HSC outputs a partition which is better than a random guess if the sum of edge weights (to be explained later) is $\Omega(n)$; (2) HSC outputs a partition which coincides with the hidden partition except for a vanishing fraction of nodes if the sum of edge weights is $\omega(n)$; and (3) HSCLR exactly recovers the hidden partition if the sum of edge weights is on the order of $n \log n$. Our results improve upon the state of the arts recently established under the model and they firstly settle the order-wise optimal results for the binary edge weight case. Moreover, we show that our results lead to efficient sketching algorithms for subspace clustering, a computer vision application. Lastly, we show that HSCLR achieves the information-theoretic limits for a special yet practically relevant model, thereby showing no computational barrier for the case.

Community Recovery in Hypergraphs

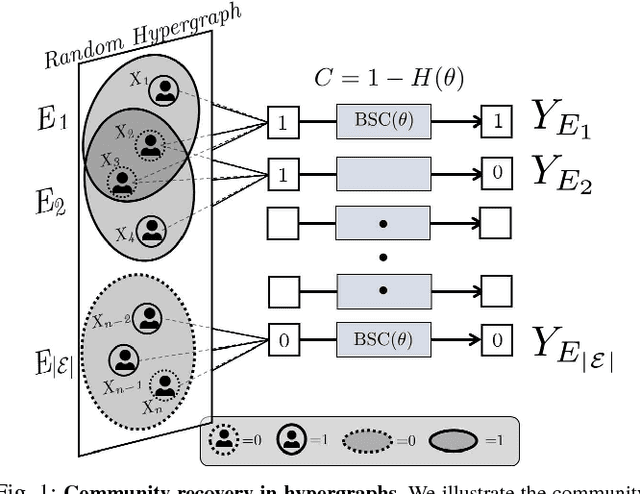
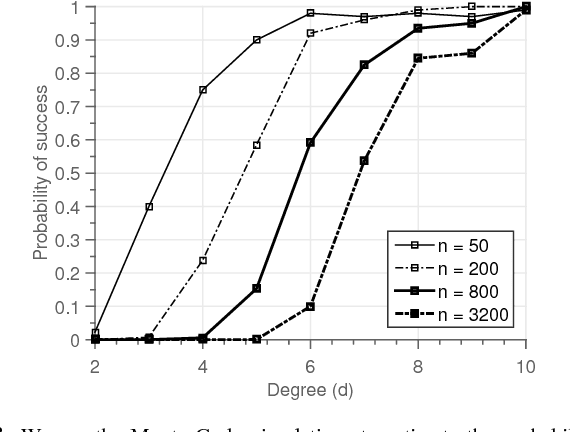
Community recovery is a central problem that arises in a wide variety of applications such as network clustering, motion segmentation, face clustering and protein complex detection. The objective of the problem is to cluster data points into distinct communities based on a set of measurements, each of which is associated with the values of a certain number of data points. While most of the prior works focus on a setting in which the number of data points involved in a measurement is two, this work explores a generalized setting in which the number can be more than two. Motivated by applications particularly in machine learning and channel coding, we consider two types of measurements: (1) homogeneity measurement which indicates whether or not the associated data points belong to the same community; (2) parity measurement which denotes the modulo-2 sum of the values of the data points. Such measurements are possibly corrupted by Bernoulli noise. We characterize the fundamental limits on the number of measurements required to reconstruct the communities for the considered models.

Community Recovery in Graphs with Locality

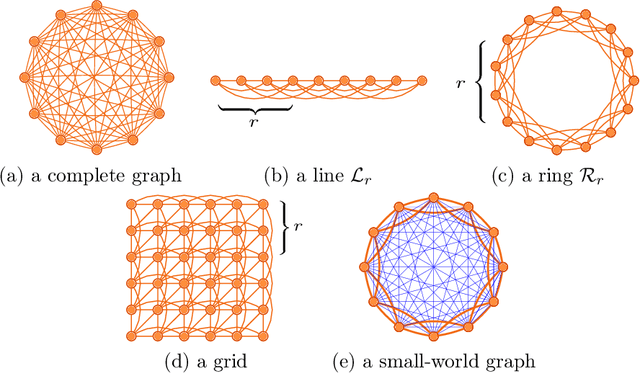
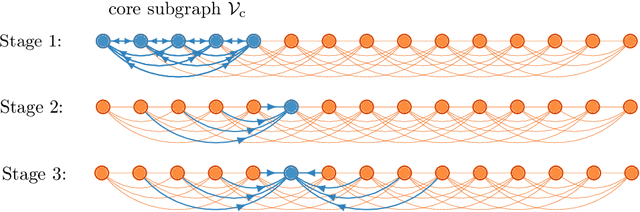
Motivated by applications in domains such as social networks and computational biology, we study the problem of community recovery in graphs with locality. In this problem, pairwise noisy measurements of whether two nodes are in the same community or different communities come mainly or exclusively from nearby nodes rather than uniformly sampled between all nodes pairs, as in most existing models. We present an algorithm that runs nearly linearly in the number of measurements and which achieves the information theoretic limit for exact recovery.

Information Recovery from Pairwise Measurements

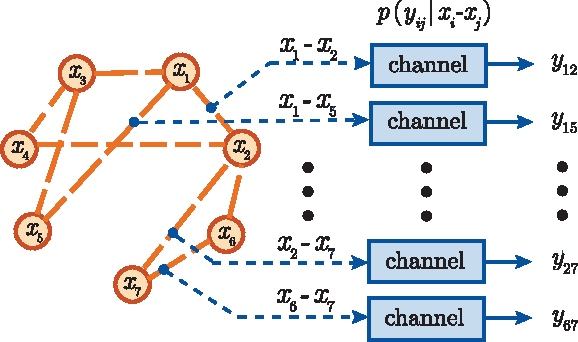
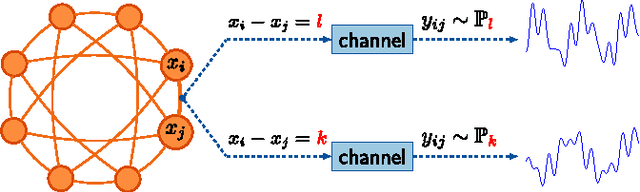
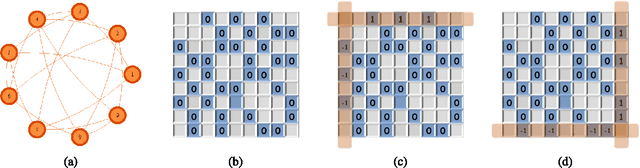
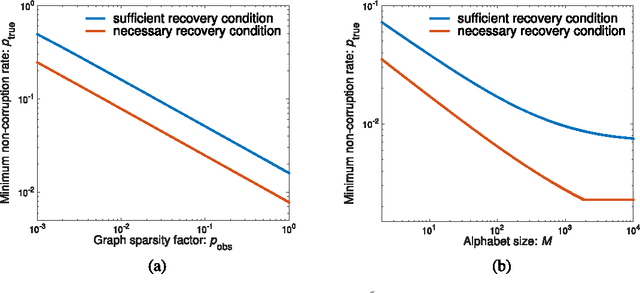
This paper is concerned with jointly recovering $n$ node-variables $\left\{ x_{i}\right\}_{1\leq i\leq n}$ from a collection of pairwise difference measurements. Imagine we acquire a few observations taking the form of $x_{i}-x_{j}$; the observation pattern is represented by a measurement graph $\mathcal{G}$ with an edge set $\mathcal{E}$ such that $x_{i}-x_{j}$ is observed if and only if $(i,j)\in\mathcal{E}$. To account for noisy measurements in a general manner, we model the data acquisition process by a set of channels with given input/output transition measures. Employing information-theoretic tools applied to channel decoding problems, we develop a \emph{unified} framework to characterize the fundamental recovery criterion, which accommodates general graph structures, alphabet sizes, and channel transition measures. In particular, our results isolate a family of \emph{minimum} \emph{channel divergence measures} to characterize the degree of measurement corruption, which together with the size of the minimum cut of $\mathcal{G}$ dictates the feasibility of exact information recovery. For various homogeneous graphs, the recovery condition depends almost only on the edge sparsity of the measurement graph irrespective of other graphical metrics; alternatively, the minimum sample complexity required for these graphs scales like \[ \text{minimum sample complexity }\asymp\frac{n\log n}{\mathsf{Hel}_{1/2}^{\min}} \] for certain information metric $\mathsf{Hel}_{1/2}^{\min}$ defined in the main text, as long as the alphabet size is not super-polynomial in $n$. We apply our general theory to three concrete applications, including the stochastic block model, the outlier model, and the haplotype assembly problem. Our theory leads to order-wise tight recovery conditions for all these scenarios.

Top-$K$ Ranking from Pairwise Comparisons: When Spectral Ranking is Optimal

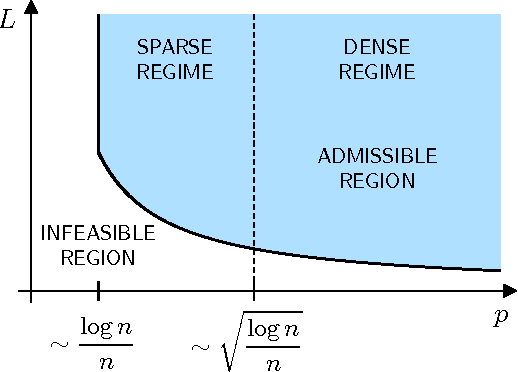
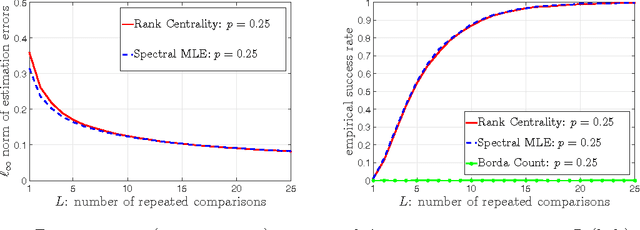
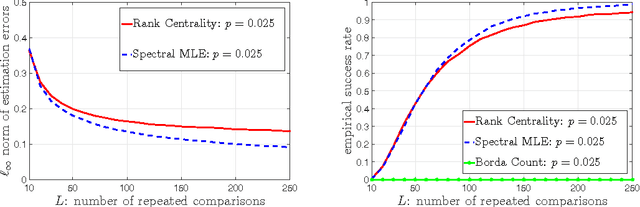
We explore the top-$K$ rank aggregation problem. Suppose a collection of items is compared in pairs repeatedly, and we aim to recover a consistent ordering that focuses on the top-$K$ ranked items based on partially revealed preference information. We investigate the Bradley-Terry-Luce model in which one ranks items according to their perceived utilities modeled as noisy observations of their underlying true utilities. Our main contributions are two-fold. First, in a general comparison model where item pairs to compare are given a priori, we attain an upper and lower bound on the sample size for reliable recovery of the top-$K$ ranked items. Second, more importantly, extending the result to a random comparison model where item pairs to compare are chosen independently with some probability, we show that in slightly restricted regimes, the gap between the derived bounds reduces to a constant factor, hence reveals that a spectral method can achieve the minimax optimality on the (order-wise) sample size required for top-$K$ ranking. That is to say, we demonstrate a spectral method alone to be sufficient to achieve the optimality and advantageous in terms of computational complexity, as it does not require an additional stage of maximum likelihood estimation that a state-of-the-art scheme employs to achieve the optimality. We corroborate our main results by numerical experiments.

Adversarial Top-$K$ Ranking

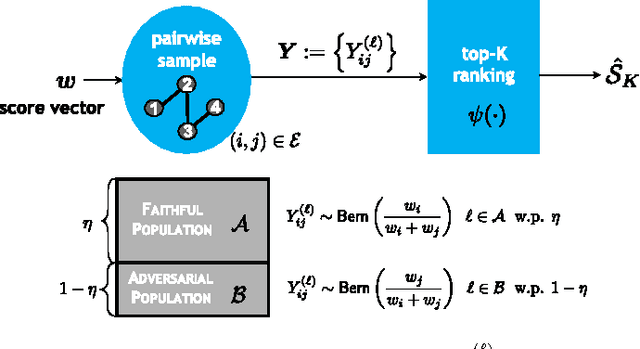
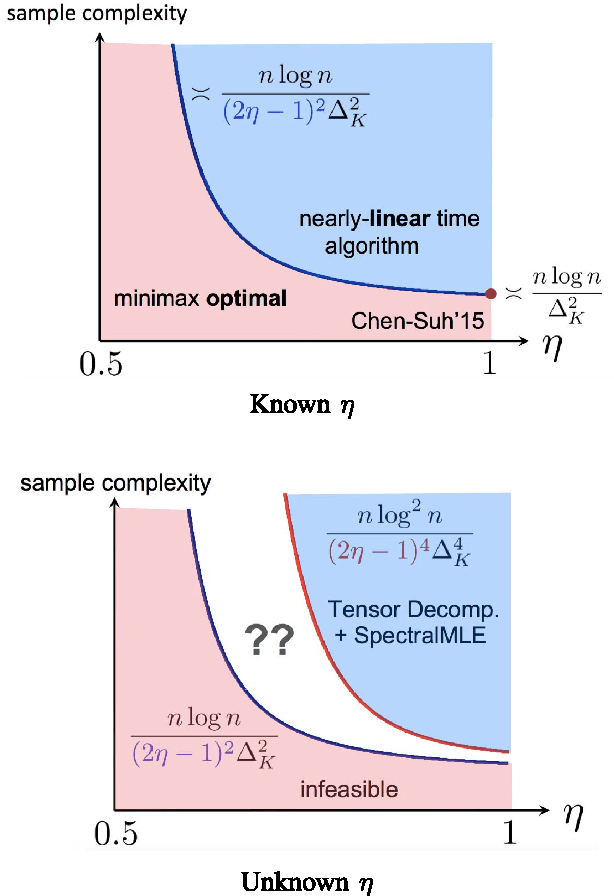
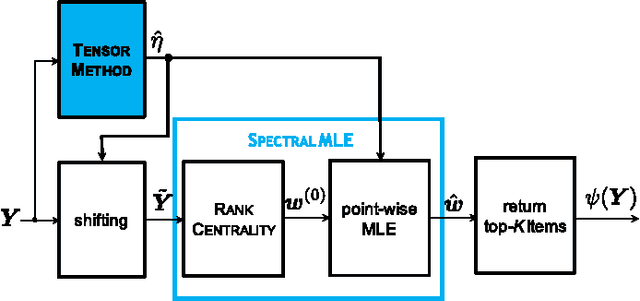
We study the top-$K$ ranking problem where the goal is to recover the set of top-$K$ ranked items out of a large collection of items based on partially revealed preferences. We consider an adversarial crowdsourced setting where there are two population sets, and pairwise comparison samples drawn from one of the populations follow the standard Bradley-Terry-Luce model (i.e., the chance of item $i$ beating item $j$ is proportional to the relative score of item $i$ to item $j$), while in the other population, the corresponding chance is inversely proportional to the relative score. When the relative size of the two populations is known, we characterize the minimax limit on the sample size required (up to a constant) for reliably identifying the top-$K$ items, and demonstrate how it scales with the relative size. Moreover, by leveraging a tensor decomposition method for disambiguating mixture distributions, we extend our result to the more realistic scenario in which the relative population size is unknown, thus establishing an upper bound on the fundamental limit of the sample size for recovering the top-$K$ set.

Spectral MLE: Top-$K$ Rank Aggregation from Pairwise Comparisons

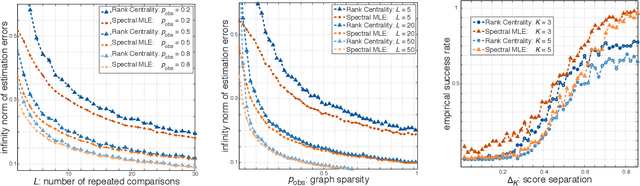
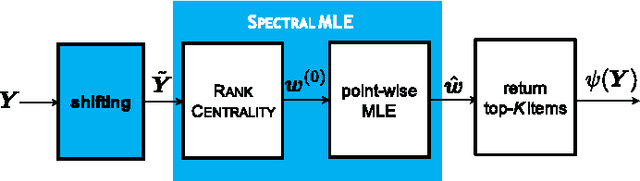
This paper explores the preference-based top-$K$ rank aggregation problem. Suppose that a collection of items is repeatedly compared in pairs, and one wishes to recover a consistent ordering that emphasizes the top-$K$ ranked items, based on partially revealed preferences. We focus on the Bradley-Terry-Luce (BTL) model that postulates a set of latent preference scores underlying all items, where the odds of paired comparisons depend only on the relative scores of the items involved. We characterize the minimax limits on identifiability of top-$K$ ranked items, in the presence of random and non-adaptive sampling. Our results highlight a separation measure that quantifies the gap of preference scores between the $K^{\text{th}}$ and $(K+1)^{\text{th}}$ ranked items. The minimum sample complexity required for reliable top-$K$ ranking scales inversely with the separation measure irrespective of other preference distribution metrics. To approach this minimax limit, we propose a nearly linear-time ranking scheme, called \emph{Spectral MLE}, that returns the indices of the top-$K$ items in accordance to a careful score estimate. In a nutshell, Spectral MLE starts with an initial score estimate with minimal squared loss (obtained via a spectral method), and then successively refines each component with the assistance of coordinate-wise MLEs. Encouragingly, Spectral MLE allows perfect top-$K$ item identification under minimal sample complexity. The practical applicability of Spectral MLE is further corroborated by numerical experiments.