Corporate Needs You to Find the Difference: Revisiting Submodular and Supermodular Ratio Optimization Problems

We study the problem of minimizing or maximizing the average value $ f(S)/|S| $ of a submodular or supermodular set function $ f: 2^V \to \mathbb{R} $ over non-empty subsets $ S \subseteq V $. This generalizes classical problems such as Densest Subgraph (DSG), Densest Supermodular Set (DSS), and Submodular Function Minimization (SFM). Motivated by recent applications, we introduce two broad formulations: Unrestricted Sparsest Submodular Set (USSS) and Unrestricted Densest Supermodular Set (UDSS), which allow for negative and non-monotone functions. We show that DSS, SFM, USSS, UDSS, and the Minimum Norm Point (MNP) problem are equivalent under strongly polynomial-time reductions, enabling algorithmic crossover. In particular, viewing these through the lens of the MNP in the base polyhedron, we connect Fujishige's theory with dense decomposition, and show that both Fujishige-Wolfe's algorithm and the heuristic \textsc{SuperGreedy++} act as universal solvers for all these problems, including sub-modular function minimization. Theoretically, we explain why \textsc{SuperGreedy++} is effective beyond DSS, including for tasks like submodular minimization and minimum $ s $-$ t $ cut. Empirically, we test several solvers, including the Fujishige-Wolfe algorithm on over 400 experiments across seven problem types and large-scale real/synthetic datasets. Surprisingly, general-purpose convex and flow-based methods outperform task-specific baselines, demonstrating that with the right framing, general optimization techniques can be both scalable and state-of-the-art for submodular and supermodular ratio problems.

Bicriteria Approximation Algorithms for Priority Matroid Median

Fairness considerations have motivated new clustering problems and algorithms in recent years. In this paper we consider the Priority Matroid Median problem which generalizes the Priority $k$-Median problem that has recently been studied. The input consists of a set of facilities $\mathcal{F}$ and a set of clients $\mathcal{C}$ that lie in a metric space $(\mathcal{F} \cup \mathcal{C},d)$, and a matroid $\mathcal{M}=(\mathcal{F},\mathcal{I})$ over the facilities. In addition each client $j$ has a specified radius $r_j \ge 0$ and each facility $i \in \mathcal{F}$ has an opening cost $f_i$. The goal is to choose a subset $S \subseteq \mathcal{F}$ of facilities to minimize the $\sum_{i \in \mathcal{F}} f_i + \sum_{j \in \mathcal{C}} d(j,S)$ subject to two constraints: (i) $S$ is an independent set in $\mathcal{M}$ (that is $S \in \mathcal{I}$) and (ii) for each client $j$, its distance to an open facility is at most $r_j$ (that is, $d(j,S) \le r_j$). For this problem we describe the first bicriteria $(c_1,c_2)$ approximations for fixed constants $c_1,c_2$: the radius constraints of the clients are violated by at most a factor of $c_1$ and the objective cost is at most $c_2$ times the optimum cost. We also improve the previously known bicriteria approximation for the uniform radius setting ($r_j := L$ $\forall j \in \mathcal{C}$).

Revisiting Priority $k$-Center: Fairness and Outliers

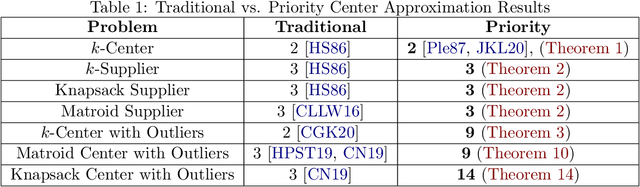
In the Priority $k$-Center problem, the input consists of a metric space $(X,d)$, an integer $k$ and for each point $v \in X$ a priority radius $r(v)$. The goal is to choose $k$-centers $S \subseteq X$ to minimize $\max_{v \in X} \frac{1}{r(v)} d(v,S)$. If all $r(v)$'s were uniform, one obtains the classical $k$-center problem. Plesn\'ik [Plesn\'ik, Disc. Appl. Math. 1987] introduced this problem and gave a $2$-approximation algorithm matching the best possible algorithm for vanilla $k$-center. We show how the problem is related to two different notions of fair clustering [Harris et al., NeurIPS 2018; Jung et al., FORC 2020]. Motivated by these developments we revisit the problem and, in our main technical contribution, develop a framework that yields constant factor approximation algorithms for Priority $k$-Center with outliers. Our framework extends to generalizations of Priority $k$-Center to matroid and knapsack constraints, and as a corollary, also yields algorithms with fairness guarantees in the lottery model of Harris et al.