RQR3D: Reparametrizing the regression targets for BEV-based 3D object detection

Accurate, fast, and reliable 3D perception is essential for autonomous driving. Recently, bird's-eye view (BEV)-based perception approaches have emerged as superior alternatives to perspective-based solutions, offering enhanced spatial understanding and more natural outputs for planning. Existing BEV-based 3D object detection methods, typically adhering to angle-based representation, directly estimate the size and orientation of rotated bounding boxes. We observe that BEV-based 3D object detection is analogous to aerial oriented object detection, where angle-based methods are recognized for being affected by discontinuities in their loss functions. Drawing inspiration from this domain, we propose Restricted Quadrilateral Representation to define 3D regression targets. RQR3D regresses the smallest horizontal bounding box encapsulating the oriented box, along with the offsets between the corners of these two boxes, thereby transforming the oriented object detection problem into a keypoint regression task. RQR3D is compatible with any 3D object detection approach. We employ RQR3D within an anchor-free single-stage object detection method and introduce an objectness head to address class imbalance problem. Furthermore, we introduce a simplified radar fusion backbone that eliminates the need for voxel grouping and processes the BEV-mapped point cloud with standard 2D convolutions, rather than sparse convolutions. Extensive evaluations on the nuScenes dataset demonstrate that RQR3D achieves state-of-the-art performance in camera-radar 3D object detection, outperforming the previous best method by +4% in NDS and +2.4% in mAP, and significantly reducing the translation and orientation errors, which are crucial for safe autonomous driving. These consistent gains highlight the robustness, precision, and real-world readiness of our approach.

Convolutional Neural Networks Analyzed via Inverse Problem Theory and Sparse Representations

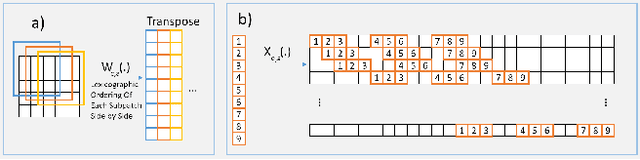
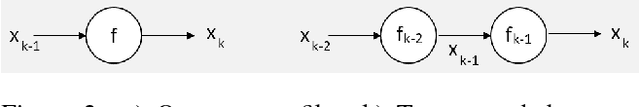
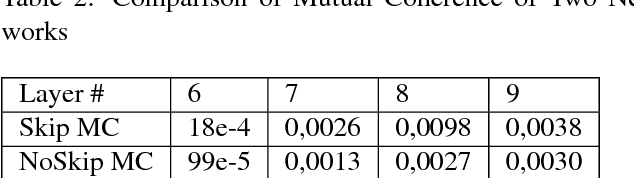
Inverse problems in imaging such as denoising, deblurring, superresolution (SR) have been addressed for many decades. In recent years, convolutional neural networks (CNNs) have been widely used for many inverse problem areas. Although their indisputable success, CNNs are not mathematically validated as to how and what they learn. In this paper, we prove that during training, CNN elements solve for inverse problems which are optimum solutions stored as CNN neuron filters. We discuss the necessity of mutual coherence between CNN layer elements in order for a network to converge to the optimum solution. We prove that required mutual coherence can be provided by the usage of residual learning and skip connections. We have set rules over training sets and depth of networks for better convergence, i.e. performance.