How do Probabilistic Graphical Models and Graph Neural Networks Look at Network Data?

Graphs are a powerful data structure for representing relational data and are widely used to describe complex real-world systems. Probabilistic Graphical Models (PGMs) and Graph Neural Networks (GNNs) can both leverage graph-structured data, but their inherent functioning is different. The question is how do they compare in capturing the information contained in networked datasets? We address this objective by solving a link prediction task and we conduct three main experiments, on both synthetic and real networks: one focuses on how PGMs and GNNs handle input features, while the other two investigate their robustness to noisy features and increasing heterophily of the graph. PGMs do not necessarily require features on nodes, while GNNs cannot exploit the network edges alone, and the choice of input features matters. We find that GNNs are outperformed by PGMs when input features are low-dimensional or noisy, mimicking many real scenarios where node attributes might be scalar or noisy. Then, we find that PGMs are more robust than GNNs when the heterophily of the graph is increased. Finally, to assess performance beyond prediction tasks, we also compare the two frameworks in terms of their computational complexity and interpretability.

Broad Spectrum Structure Discovery in Large-Scale Higher-Order Networks

Complex systems are often driven by higher-order interactions among multiple units, naturally represented as hypergraphs. Understanding dependency structures within these hypergraphs is crucial for understanding and predicting the behavior of complex systems but is made challenging by their combinatorial complexity and computational demands. In this paper, we introduce a class of probabilistic models that efficiently represents and discovers a broad spectrum of mesoscale structure in large-scale hypergraphs. The key insight enabling this approach is to treat classes of similar units as themselves nodes in a latent hypergraph. By modeling observed node interactions through latent interactions among classes using low-rank representations, our approach tractably captures rich structural patterns while ensuring model identifiability. This allows for direct interpretation of distinct node- and class-level structures. Empirically, our model improves link prediction over state-of-the-art methods and discovers interpretable structures in diverse real-world systems, including pharmacological and social networks, advancing the ability to incorporate large-scale higher-order data into the scientific process.

Flexible inference in heterogeneous and attributed multilayer networks

Networked datasets are often enriched by different types of information about individual nodes or edges. However, most existing methods for analyzing such datasets struggle to handle the complexity of heterogeneous data, often requiring substantial model-specific analysis. In this paper, we develop a probabilistic generative model to perform inference in multilayer networks with arbitrary types of information. Our approach employs a Bayesian framework combined with the Laplace matching technique to ease interpretation of inferred parameters. Furthermore, the algorithmic implementation relies on automatic differentiation, avoiding the need for explicit derivations. This makes our model scalable and flexible to adapt to any combination of input data. We demonstrate the effectiveness of our method in detecting overlapping community structures and performing various prediction tasks on heterogeneous multilayer data, where nodes and edges have different types of attributes. Additionally, we showcase its ability to unveil a variety of patterns in a social support network among villagers in rural India by effectively utilizing all input information in a meaningful way.

Hypergraphs with node attributes: structure and inference

Many networked datasets with units interacting in groups of two or more, encoded with hypergraphs, are accompanied by extra information about nodes, such as the role of an individual in a workplace. Here we show how these node attributes can be used to improve our understanding of the structure resulting from higher-order interactions. We consider the problem of community detection in hypergraphs and develop a principled model that combines higher-order interactions and node attributes to better represent the observed interactions and to detect communities more accurately than using either of these types of information alone. The method learns automatically from the input data the extent to which structure and attributes contribute to explain the data, down weighing or discarding attributes if not informative. Our algorithmic implementation is efficient and scales to large hypergraphs and interactions of large numbers of units. We apply our method to a variety of systems, showing strong performance in hyperedge prediction tasks and in selecting community divisions that correlate with attributes when these are informative, but discarding them otherwise. Our approach illustrates the advantage of using informative node attributes when available with higher-order data.

A model for efficient dynamical ranking in networks

We present a physics-inspired method for inferring dynamic rankings in directed temporal networks - networks in which each directed and timestamped edge reflects the outcome and timing of a pairwise interaction. The inferred ranking of each node is real-valued and varies in time as each new edge, encoding an outcome like a win or loss, raises or lowers the node's estimated strength or prestige, as is often observed in real scenarios including sequences of games, tournaments, or interactions in animal hierarchies. Our method works by solving a linear system of equations and requires only one parameter to be tuned. As a result, the corresponding algorithm is scalable and efficient. We test our method by evaluating its ability to predict interactions (edges' existence) and their outcomes (edges' directions) in a variety of applications, including both synthetic and real data. Our analysis shows that in many cases our method's performance is better than existing methods for predicting dynamic rankings and interaction outcomes.

Immiscible Color Flows in Optimal Transport Networks for Image Classification

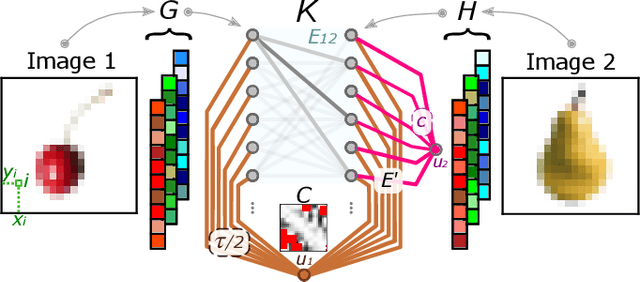
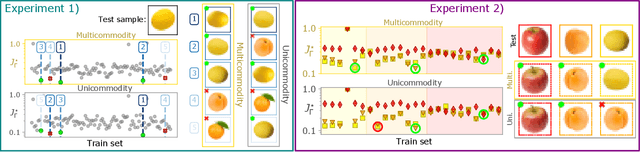
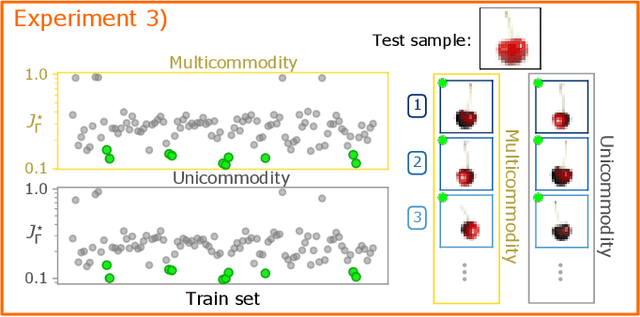
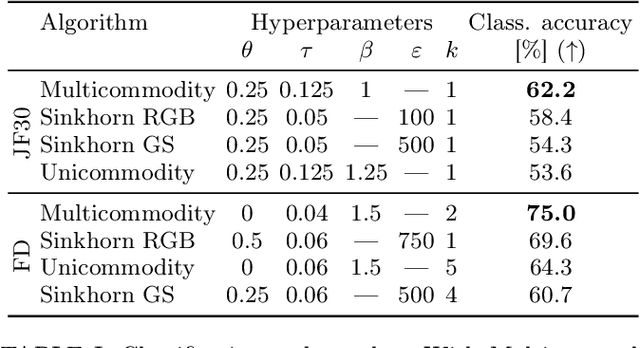
In classification tasks, it is crucial to meaningfully exploit information contained in data. Here, we propose a physics-inspired dynamical system that adapts Optimal Transport principles to effectively leverage color distributions of images. Our dynamics regulates immiscible fluxes of colors traveling on a network built from images. Instead of aggregating colors together, it treats them as different commodities that interact with a shared capacity on edges. Our method outperforms competitor algorithms on image classification tasks in datasets where color information matters.

Principled inference of hyperedges and overlapping communities in hypergraphs

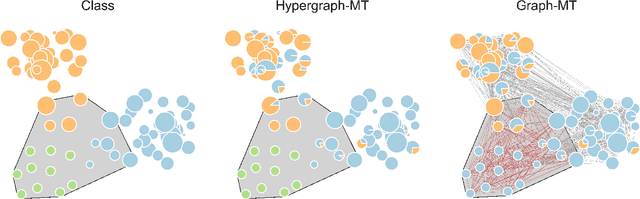
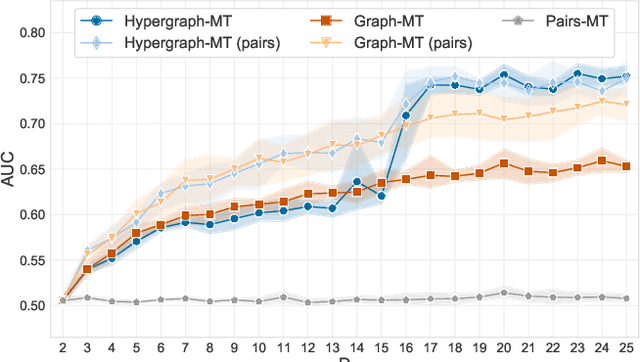
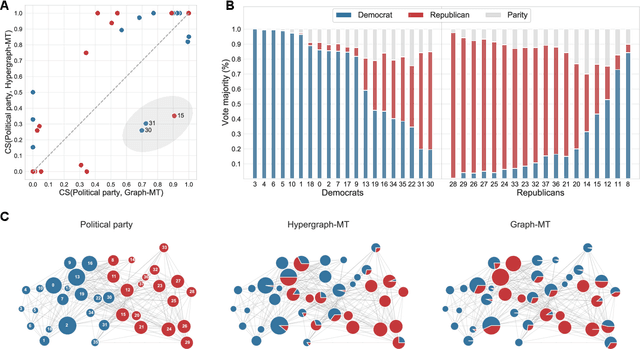
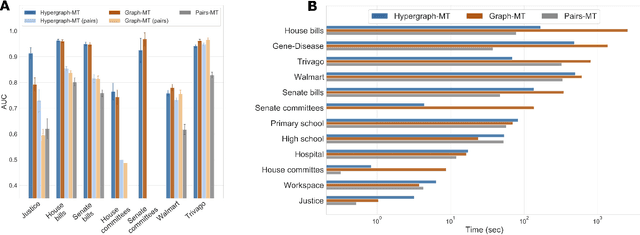
Hypergraphs, encoding structured interactions among any number of system units, have recently proven a successful tool to describe many real-world biological and social networks. Here we propose a framework based on statistical inference to characterize the structural organization of hypergraphs. The method allows to infer missing hyperedges of any size in a principled way, and to jointly detect overlapping communities in presence of higher-order interactions. Furthermore, our model has an efficient numerical implementation, and it runs faster than dyadic algorithms on pairwise records projected from higher-order data. We apply our method to a variety of real-world systems, showing strong performance in hyperedge prediction tasks, detecting communities well aligned with the information carried by interactions, and robustness against addition of noisy hyperedges. Our approach illustrates the fundamental advantages of a hypergraph probabilistic model when modeling relational systems with higher-order interactions.

Estimating Social Influence from Observational Data

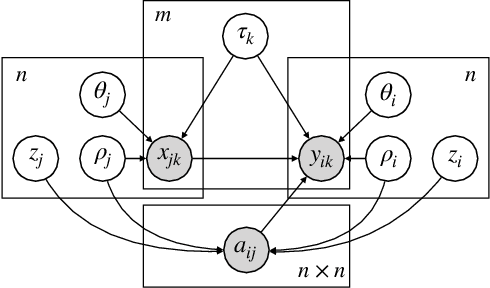
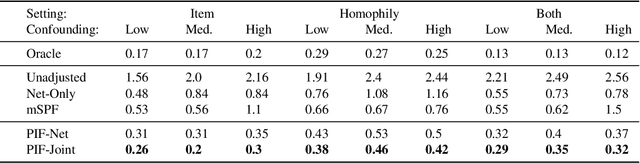
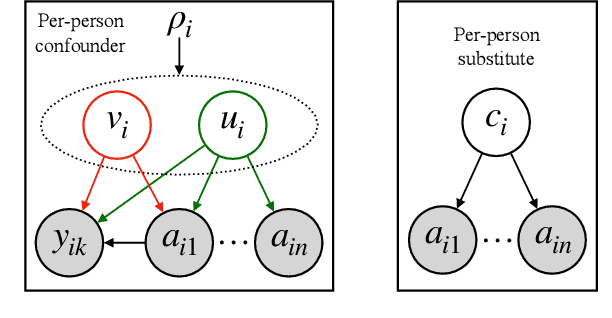
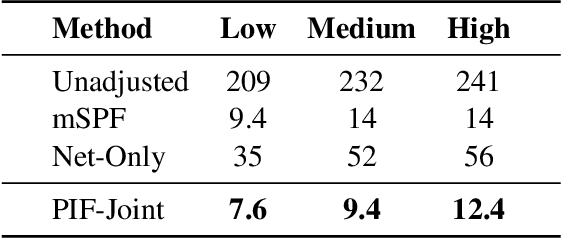
We consider the problem of estimating social influence, the effect that a person's behavior has on the future behavior of their peers. The key challenge is that shared behavior between friends could be equally explained by influence or by two other confounding factors: 1) latent traits that caused people to both become friends and engage in the behavior, and 2) latent preferences for the behavior. This paper addresses the challenges of estimating social influence with three contributions. First, we formalize social influence as a causal effect, one which requires inferences about hypothetical interventions. Second, we develop Poisson Influence Factorization (PIF), a method for estimating social influence from observational data. PIF fits probabilistic factor models to networks and behavior data to infer variables that serve as substitutes for the confounding latent traits. Third, we develop assumptions under which PIF recovers estimates of social influence. We empirically study PIF with semi-synthetic and real data from Last.fm, and conduct a sensitivity analysis. We find that PIF estimates social influence most accurately compared to related methods and remains robust under some violations of its assumptions.

The interplay between ranking and communities in networks

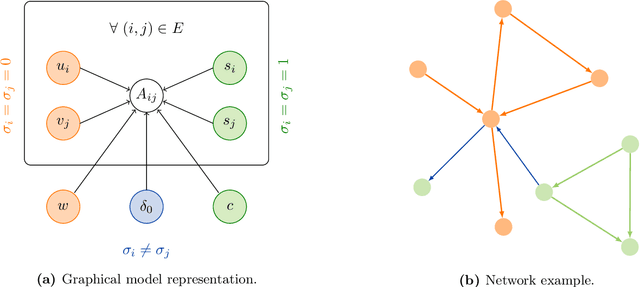
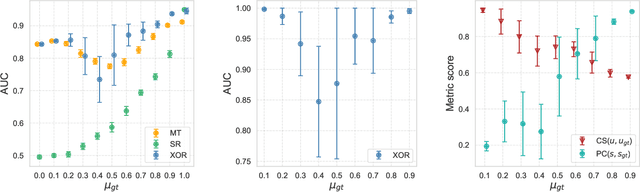
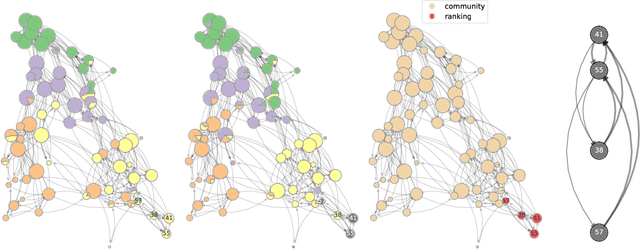
Community detection and hierarchy extraction are usually thought of as separate inference tasks on networks. Considering only one of the two when studying real-world data can be an oversimplification. In this work, we present a generative model based on an interplay between community and hierarchical structures. It assumes that each node has a preference in the interaction mechanism and nodes with the same preference are more likely to interact, while heterogeneous interactions are still allowed. The algorithmic implementation is efficient, as it exploits the sparsity of network datasets. We demonstrate our method on synthetic and real-world data and compare performance with two standard approaches for community detection and ranking extraction. We find that the algorithm accurately retrieves each node's preference in different scenarios and we show that it can distinguish small subsets of nodes that behave differently than the majority. As a consequence, the model can recognise whether a network has an overall preferred interaction mechanism. This is relevant in situations where there is no clear "a priori" information about what structure explains the observed network datasets well. Our model allows practitioners to learn this automatically from the data.

Optimal transport in multilayer networks

Modeling traffic distribution and extracting optimal flows in multilayer networks is of utmost importance to design efficient multi-modal network infrastructures. Recent results based on optimal transport theory provide powerful and computationally efficient methods to address this problem, but they are mainly focused on modeling single-layer networks. Here we adapt these results to study how optimal flows distribute on multilayer networks. We propose a model where optimal flows on different layers contribute differently to the total cost to be minimized. This is done by means of a parameter that varies with layers, which allows to flexibly tune the sensitivity to traffic congestion of the various layers. As an application, we consider transportation networks, where each layer is associated to a different transportation system and show how the traffic distribution varies as we tune this parameter across layers. We show an example of this result on the real 2-layer network of the city of Bordeaux with bus and tram, where we find that in certain regimes the presence of the tram network significantly unburdens the traffic on the road network. Our model paves the way to further analysis of optimal flows and navigability strategies in real multilayer networks.