Spectral Differential Network Analysis for High-Dimensional Time Series

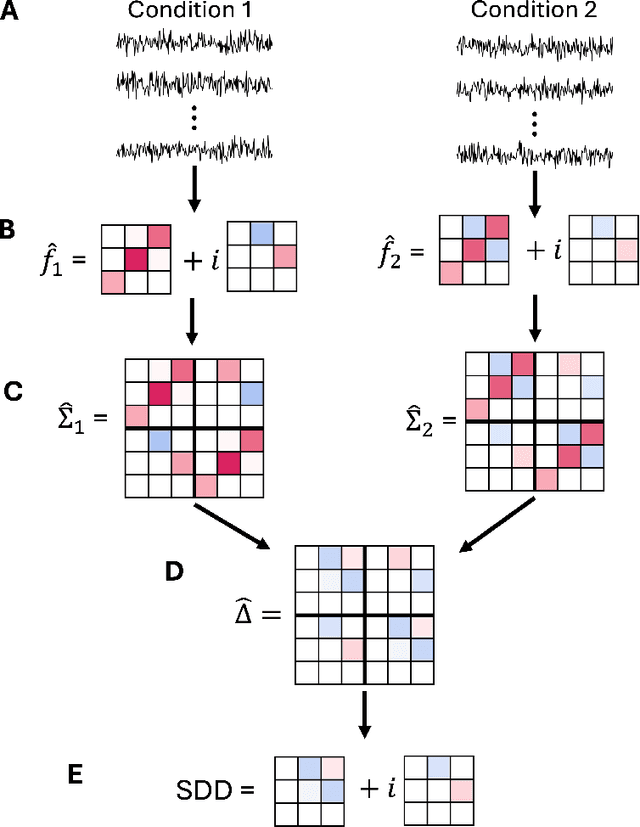
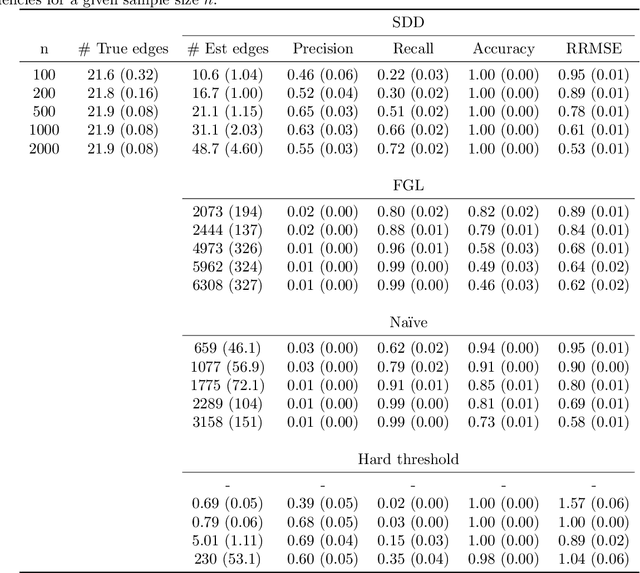
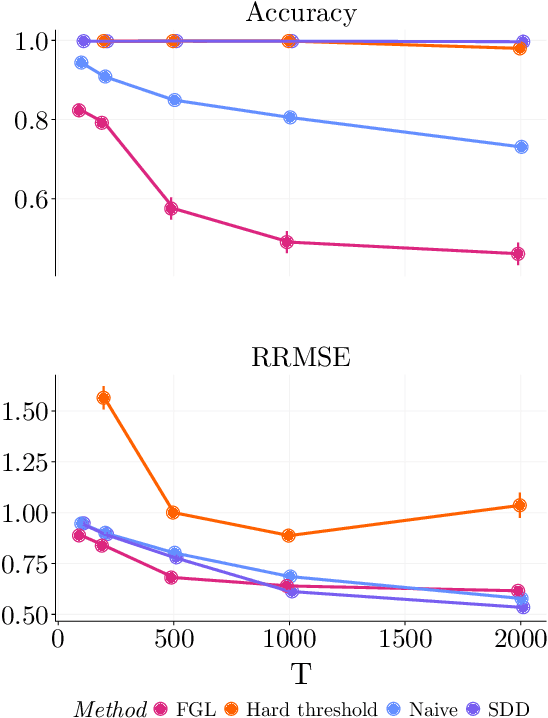
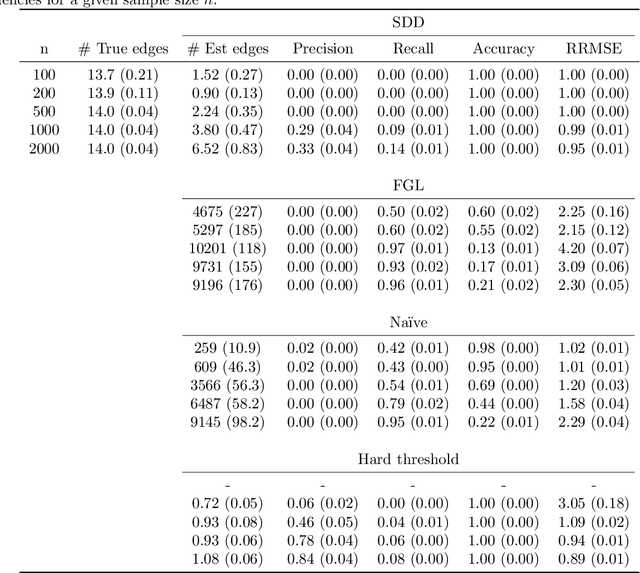
Spectral networks derived from multivariate time series data arise in many domains, from brain science to Earth science. Often, it is of interest to study how these networks change under different conditions. For instance, to better understand epilepsy, it would be interesting to capture the changes in the brain connectivity network as a patient experiences a seizure, using electroencephalography data. A common approach relies on estimating the networks in each condition and calculating their difference. Such estimates may behave poorly in high dimensions as the networks themselves may not be sparse in structure while their difference may be. We build upon this observation to develop an estimator of the difference in inverse spectral densities across two conditions. Using an L1 penalty on the difference, consistency is established by only requiring the difference to be sparse. We illustrate the method on synthetic data experiments, on experiments with electroencephalography data, and on experiments with optogentic stimulation and micro-electrocorticography data.

Black box tests for algorithmic stability

Algorithmic stability is a concept from learning theory that expresses the degree to which changes to the input data (e.g., removal of a single data point) may affect the outputs of a regression algorithm. Knowing an algorithm's stability properties is often useful for many downstream applications -- for example, stability is known to lead to desirable generalization properties and predictive inference guarantees. However, many modern algorithms currently used in practice are too complex for a theoretical analysis of their stability properties, and thus we can only attempt to establish these properties through an empirical exploration of the algorithm's behavior on various data sets. In this work, we lay out a formal statistical framework for this kind of "black box testing" without any assumptions on the algorithm or the data distribution, and establish fundamental bounds on the ability of any black box test to identify algorithmic stability.