Contextual Stochastic Vehicle Routing with Time Windows

We study the vehicle routing problem with time windows (VRPTW) and stochastic travel times, in which the decision-maker observes related contextual information, represented as feature variables, before making routing decisions. Despite the extensive literature on stochastic VRPs, the integration of feature variables has received limited attention in this context. We introduce the contextual stochastic VRPTW, which minimizes the total transportation cost and expected late arrival penalties conditioned on the observed features. Since the joint distribution of travel times and features is unknown, we present novel data-driven prescriptive models that use historical data to provide an approximate solution to the problem. We distinguish the prescriptive models between point-based approximation, sample average approximation, and penalty-based approximation, each taking a different perspective on dealing with stochastic travel times and features. We develop specialized branch-price-and-cut algorithms to solve these data-driven prescriptive models. In our computational experiments, we compare the out-of-sample cost performance of different methods on instances with up to one hundred customers. Our results show that, surprisingly, a feature-dependent sample average approximation outperforms existing and novel methods in most settings.

Bilevel Optimization for Feature Selection in the Data-Driven Newsvendor Problem

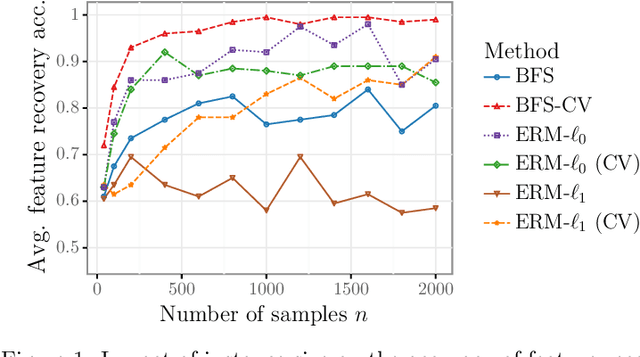
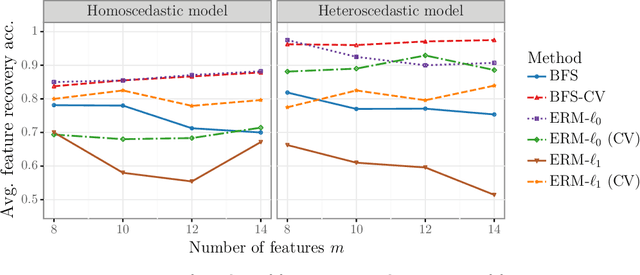
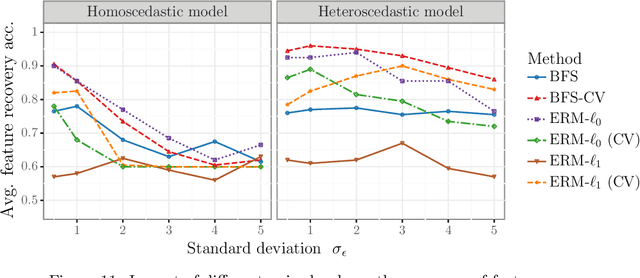
We study the feature-based newsvendor problem, in which a decision-maker has access to historical data consisting of demand observations and exogenous features. In this setting, we investigate feature selection, aiming to derive sparse, explainable models with improved out-of-sample performance. Up to now, state-of-the-art methods utilize regularization, which penalizes the number of selected features or the norm of the solution vector. As an alternative, we introduce a novel bilevel programming formulation. The upper-level problem selects a subset of features that minimizes an estimate of the out-of-sample cost of ordering decisions based on a held-out validation set. The lower-level problem learns the optimal coefficients of the decision function on a training set, using only the features selected by the upper-level. We present a mixed integer linear program reformulation for the bilevel program, which can be solved to optimality with standard optimization solvers. Our computational experiments show that the method accurately recovers ground-truth features already for instances with a sample size of a few hundred observations. In contrast, regularization-based techniques often fail at feature recovery or require thousands of observations to obtain similar accuracy. Regarding out-of-sample generalization, we achieve improved or comparable cost performance.

Support Vector Machines with the Hard-Margin Loss: Optimal Training via Combinatorial Benders' Cuts

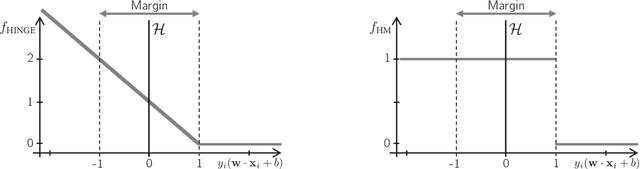
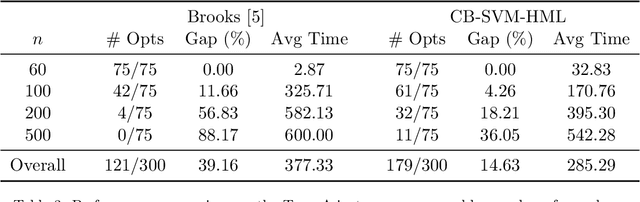
The classical hinge-loss support vector machines (SVMs) model is sensitive to outlier observations due to the unboundedness of its loss function. To circumvent this issue, recent studies have focused on non-convex loss functions, such as the hard-margin loss, which associates a constant penalty to any misclassified or within-margin sample. Applying this loss function yields much-needed robustness for critical applications but it also leads to an NP-hard model that makes training difficult, since current exact optimization algorithms show limited scalability, whereas heuristics are not able to find high-quality solutions consistently. Against this background, we propose new integer programming strategies that significantly improve our ability to train the hard-margin SVM model to global optimality. We introduce an iterative sampling and decomposition approach, in which smaller subproblems are used to separate combinatorial Benders' cuts. Those cuts, used within a branch-and-cut algorithm, permit to converge much more quickly towards a global optimum. Through extensive numerical analyses on classical benchmark data sets, our solution algorithm solves, for the first time, 117 new data sets to optimality and achieves a reduction of 50% in the average optimality gap for the hardest datasets of the benchmark.

Community Detection in the Stochastic Block Model by Mixed Integer Programming

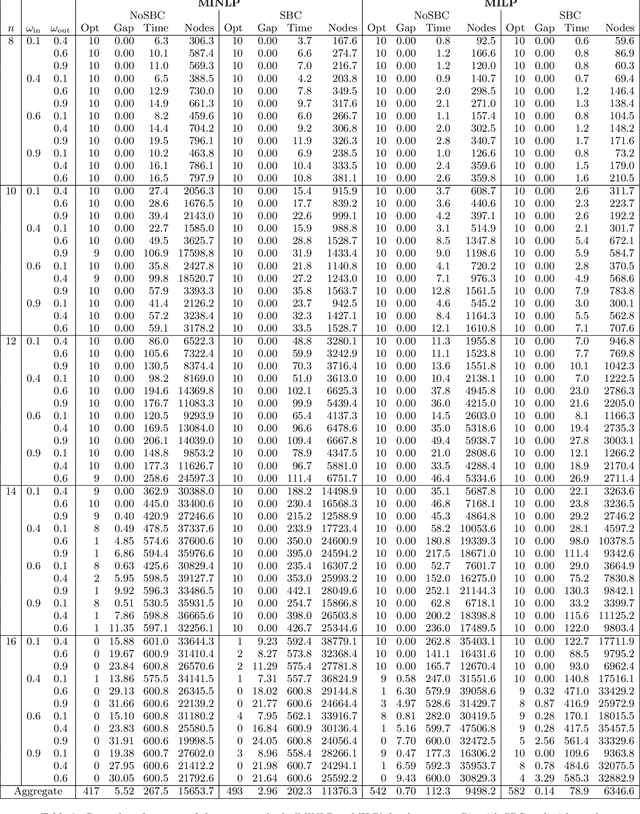
The Degree-Corrected Stochastic Block Model (DCSBM) is a popular model to generate random graphs with community structure given an expected degree sequence. The standard approach of community detection based on the DCSBM is to search for the model parameters that are the most likely to have produced the observed network data through maximum likelihood estimation (MLE). Current techniques for the MLE problem are heuristics, and therefore do not guarantee convergence to the optimum. We present mathematical programming formulations and exact solution methods that can provably find the model parameters and community assignments of maximum likelihood given an observed graph. We compare these exact methods with classical heuristic algorithms based on expectation-maximization (EM). The solutions given by exact methods give us a principled way of measuring the experimental performance of classical heuristics and comparing different variations thereof.