Perspectives on Stochastic Localization

We survey different perspectives on the stochastic localization process of [Eld13], a powerful construction that has had many exciting recent applications in high-dimensional probability and algorithm design. Unlike prior surveys on this topic, our focus is on giving a self-contained presentation of all known alternative constructions of Eldan's stochastic localization, with an emphasis on connections between different constructions. Our hope is that by collecting these perspectives, some of which had primarily arisen within a particular community (e.g., probability theory, theoretical computer science, information theory, or machine learning), we can broaden the accessibility of stochastic localization, and ease its future use.

SHRIMP: Sparser Random Feature Models via Iterative Magnitude Pruning

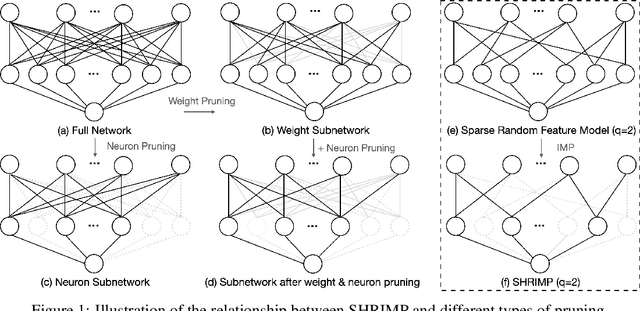
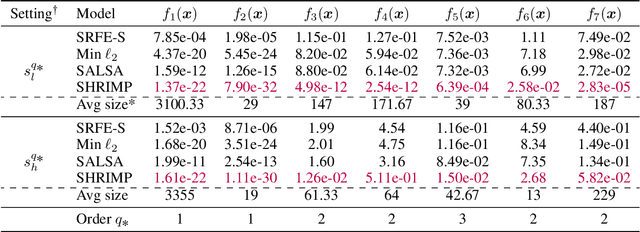
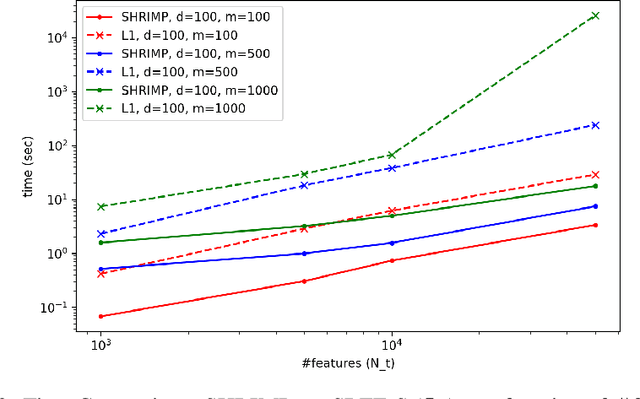
Sparse shrunk additive models and sparse random feature models have been developed separately as methods to learn low-order functions, where there are few interactions between variables, but neither offers computational efficiency. On the other hand, $\ell_2$-based shrunk additive models are efficient but do not offer feature selection as the resulting coefficient vectors are dense. Inspired by the success of the iterative magnitude pruning technique in finding lottery tickets of neural networks, we propose a new method -- Sparser Random Feature Models via IMP (ShRIMP) -- to efficiently fit high-dimensional data with inherent low-dimensional structure in the form of sparse variable dependencies. Our method can be viewed as a combined process to construct and find sparse lottery tickets for two-layer dense networks. We explain the observed benefit of SHRIMP through a refined analysis on the generalization error for thresholded Basis Pursuit and resulting bounds on eigenvalues. From function approximation experiments on both synthetic data and real-world benchmark datasets, we show that SHRIMP obtains better than or competitive test accuracy compared to state-of-art sparse feature and additive methods such as SRFE-S, SSAM, and SALSA. Meanwhile, SHRIMP performs feature selection with low computational complexity and is robust to the pruning rate, indicating a robustness in the structure of the obtained subnetworks. We gain insight into the lottery ticket hypothesis through SHRIMP by noting a correspondence between our model and weight/neuron subnetworks.