Prediction error certification for PINNs: Theory, computation, and application to Stokes flow

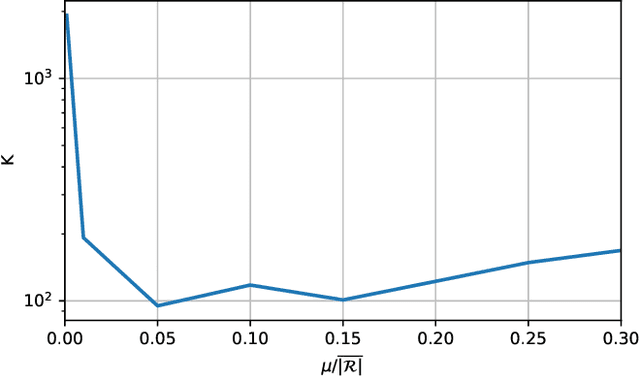
Rigorous error estimation is a fundamental topic in numerical analysis. With the increasing use of physics-informed neural networks (PINNs) for solving partial differential equations, several approaches have been developed to quantify the associated prediction error. In this work, we build upon a semigroup-based framework previously introduced by the authors for estimating the PINN error. While this estimator has so far been limited to academic examples - due to the need to compute quantities related to input-to-state stability - we extend its applicability to a significantly broader class of problems. This is accomplished by modifying the error bound and proposing numerical strategies to approximate the required stability parameters. The extended framework enables the certification of PINN predictions in more realistic scenarios, as demonstrated by a numerical study of Stokes flow around a cylinder.

Certified machine learning: Rigorous a posteriori error bounds for PDE defined PINNs

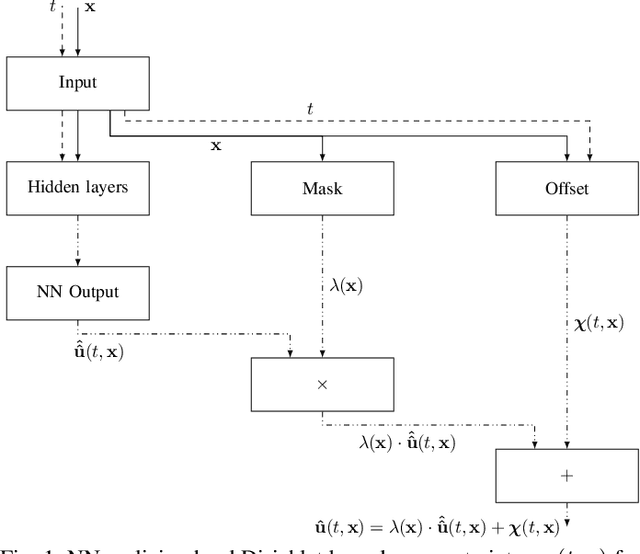
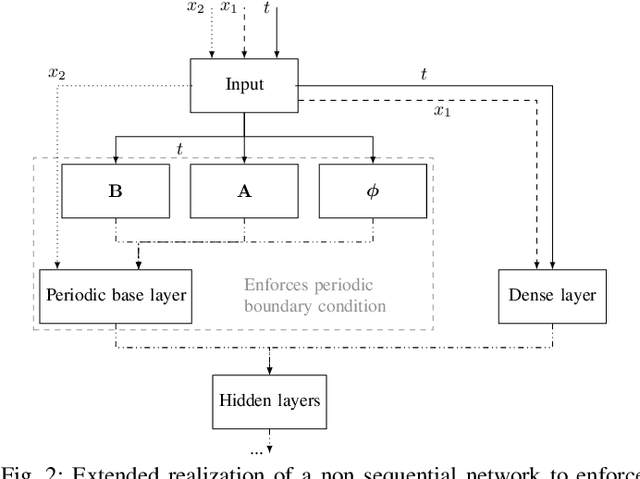
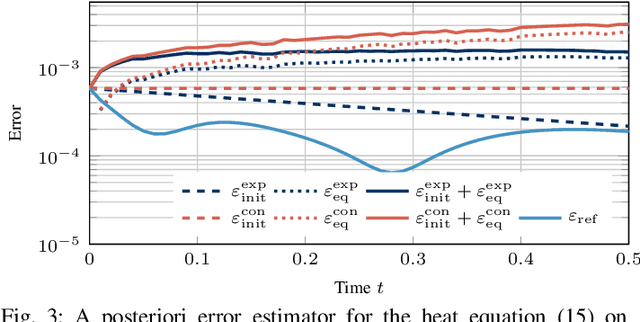
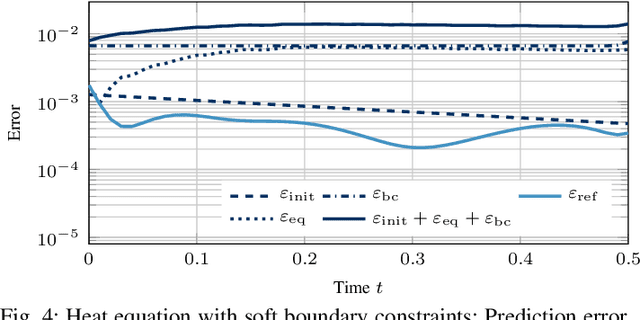
Prediction error quantification in machine learning has been left out of most methodological investigations of neural networks, for both purely data-driven and physics-informed approaches. Beyond statistical investigations and generic results on the approximation capabilities of neural networks, we present a rigorous upper bound on the prediction error of physics-informed neural networks. This bound can be calculated without the knowledge of the true solution and only with a priori available information about the characteristics of the underlying dynamical system governed by a partial differential equation. We apply this a posteriori error bound exemplarily to four problems: the transport equation, the heat equation, the Navier-Stokes equation and the Klein-Gordon equation.

Certified machine learning: A posteriori error estimation for physics-informed neural networks

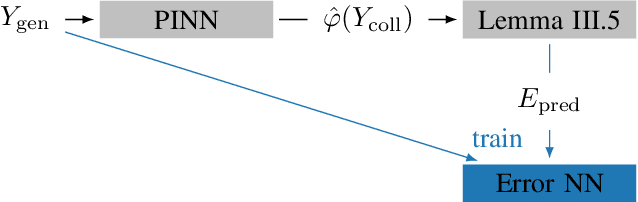
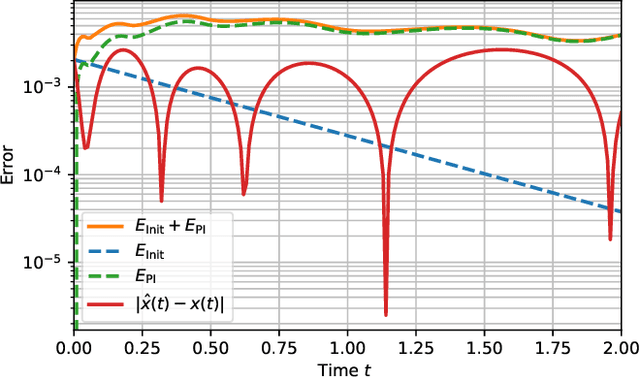
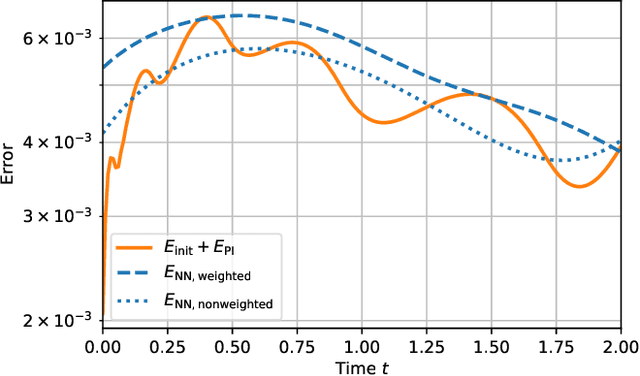
Physics-informed neural networks (PINNs) are one popular approach to introduce a priori knowledge about physical systems into the learning framework. PINNs are known to be robust for smaller training sets, derive better generalization problems, and are faster to train. In this paper, we show that using PINNs in comparison with purely data-driven neural networks is not only favorable for training performance but allows us to extract significant information on the quality of the approximated solution. Assuming that the underlying differential equation for the PINN training is an ordinary differential equation, we derive a rigorous upper limit on the PINN prediction error. This bound is applicable even for input data not included in the training phase and without any prior knowledge about the true solution. Therefore, our a posteriori error estimation is an essential step to certify the PINN. We apply our error estimator exemplarily to two academic toy problems, whereof one falls in the category of model-predictive control and thereby shows the practical use of the derived results.