Model-free algorithms for fast node clustering in SBM type graphs and application to social role inference in animals

We propose a novel family of model-free algorithms for node clustering and parameter inference in graphs generated from the Stochastic Block Model (SBM), a fundamental framework in community detection. Drawing inspiration from the Lloyd algorithm for the $k$-means problem, our approach extends to SBMs with general edge weight distributions. We establish the consistency of our estimator under a natural identifiability condition. Through extensive numerical experiments, we benchmark our methods against state-of-the-art techniques, demonstrating significantly faster computation times with the lower order of estimation error. Finally, we validate the practical relevance of our algorithms by applying them to empirical network data from behavioral ecology.

Efficient Matrix Profile Computation Using Different Distance Functions

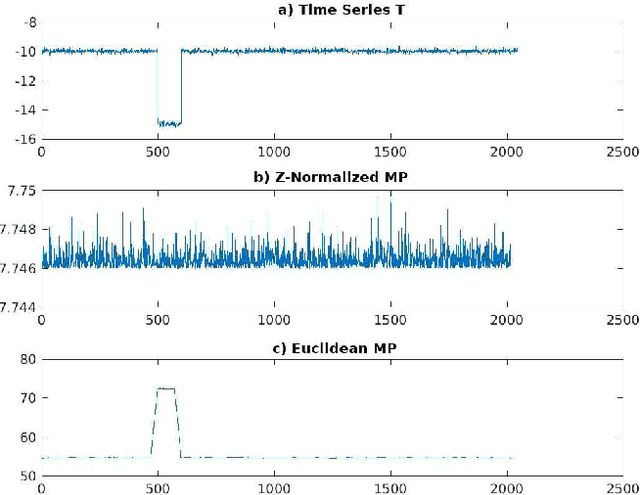
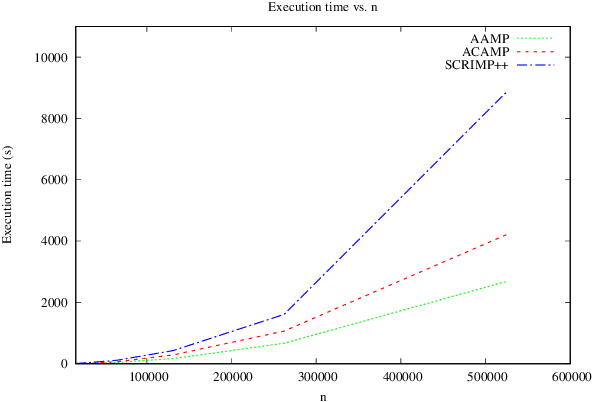
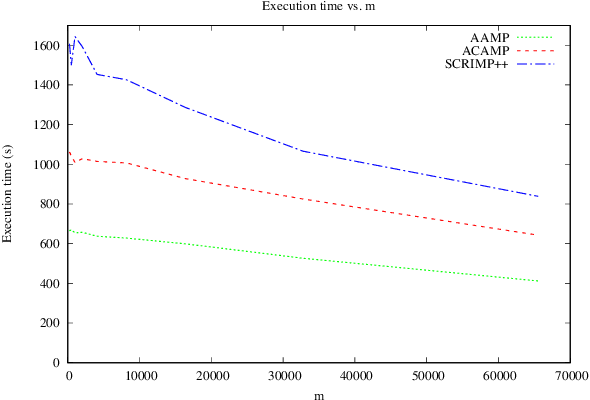
Matrix profile has been recently proposed as a promising technique to the problem of all-pairs-similarity search on time series. Efficient algorithms have been proposed for computing it, e.g., STAMP, STOMP and SCRIMP++. All these algorithms use the z-normalized Euclidean distance to measure the distance between subsequences. However, as we observed, for some datasets other Euclidean measurements are more useful for knowledge discovery from time series. In this paper, we propose efficient algorithms for computing matrix profile for a general class of Euclidean distances. We first propose a simple but efficient algorithm called AAMP for computing matrix profile with the "pure" (non-normalized) Euclidean distance. Then, we extend our algorithm for the p-norm distance. We also propose an algorithm, called ACAMP, that uses the same principle as AAMP, but for the case of z-normalized Euclidean distance. We implemented our algorithms, and evaluated their performance through experimentation. The experiments show excellent performance results. For example, they show that AAMP is very efficient for computing matrix profile for non-normalized Euclidean distances. The results also show that the ACAMP algorithm is significantly faster than SCRIMP++ (the state of the art matrix profile algorithm) for the case of z-normalized Euclidean distance.