Scalable extensions to given-data Sobol' index estimators

Given-data methods for variance-based sensitivity analysis have significantly advanced the feasibility of Sobol' index computation for computationally expensive models and models with many inputs. However, the limitations of existing methods still preclude their application to models with an extremely large number of inputs. In this work, we present practical extensions to the existing given-data Sobol' index method, which allow variance-based sensitivity analysis to be efficiently performed on large models such as neural networks, which have $>10^4$ parameterizable inputs. For models of this size, holding all input-output evaluations simultaneously in memory -- as required by existing methods -- can quickly become impractical. These extensions also support nonstandard input distributions with many repeated values, which are not amenable to equiprobable partitions employed by existing given-data methods. Our extensions include a general definition of the given-data Sobol' index estimator with arbitrary partition, a streaming algorithm to process input-output samples in batches, and a heuristic to filter out small indices that are indistinguishable from zero indices due to statistical noise. We show that the equiprobable partition employed in existing given-data methods can introduce significant bias into Sobol' index estimates even at large sample sizes and provide numerical analyses that demonstrate why this can occur. We also show that our streaming algorithm can achieve comparable accuracy and runtimes with lower memory requirements, relative to current methods which process all samples at once. We demonstrate our novel developments on two application problems in neural network modeling.

An out-of-distribution discriminator based on Bayesian neural network epistemic uncertainty

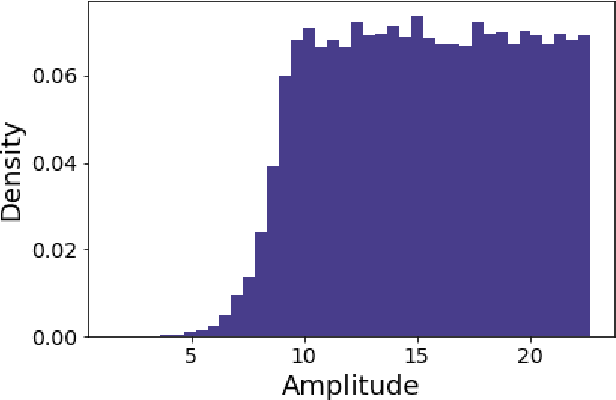
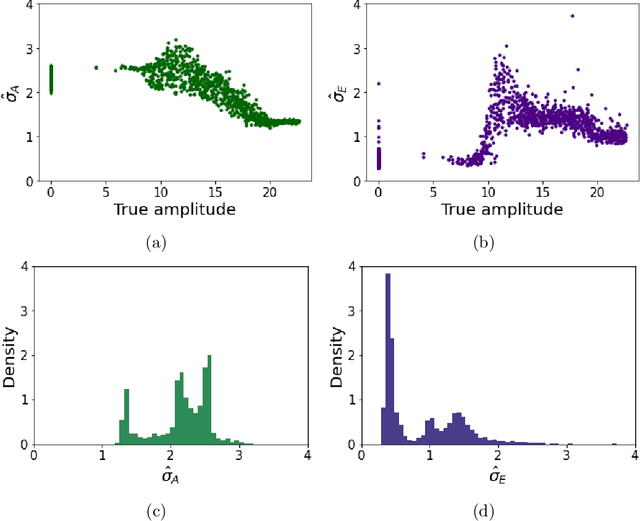
Neural networks have revolutionized the field of machine learning with increased predictive capability. In addition to improving the predictions of neural networks, there is a simultaneous demand for reliable uncertainty quantification on estimates made by machine learning methods such as neural networks. Bayesian neural networks (BNNs) are an important type of neural network with built-in capability for quantifying uncertainty. This paper discusses aleatoric and epistemic uncertainty in BNNs and how they can be calculated. With an example dataset of images where the goal is to identify the amplitude of an event in the image, it is shown that epistemic uncertainty tends to be lower in images which are well-represented in the training dataset and tends to be high in images which are not well-represented. An algorithm for out-of-distribution (OoD) detection with BNN epistemic uncertainty is introduced along with various experiments demonstrating factors influencing the OoD detection capability in a BNN. The OoD detection capability with epistemic uncertainty is shown to be comparable to the OoD detection in the discriminator network of a generative adversarial network (GAN) with comparable network architecture.