Machine Learning with Multitype Protected Attributes: Intersectional Fairness through Regularisation

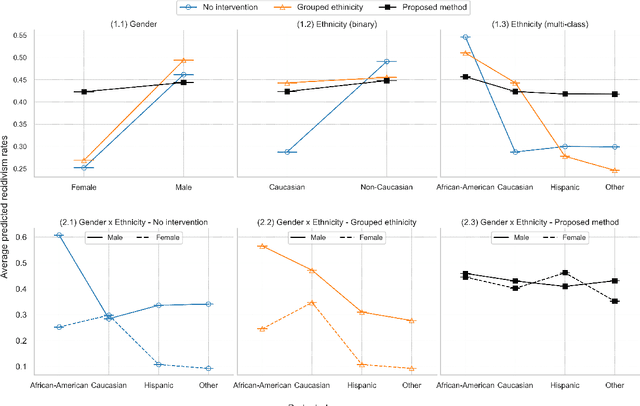
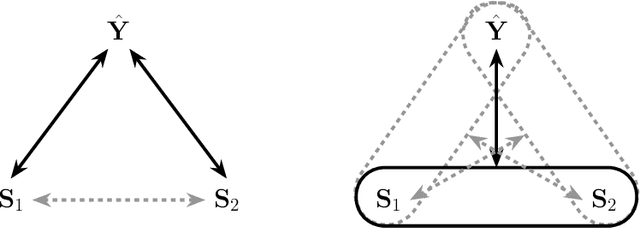
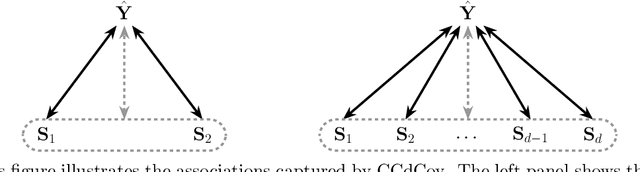
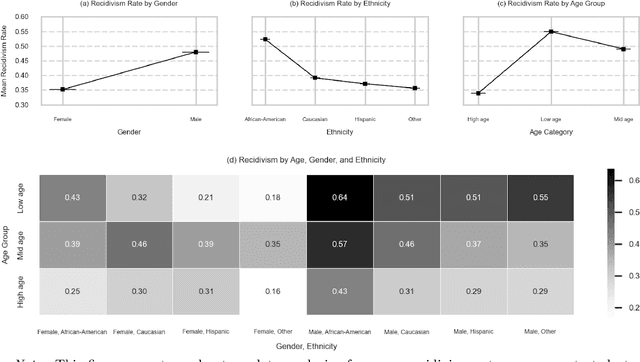
Ensuring equitable treatment (fairness) across protected attributes (such as gender or ethnicity) is a critical issue in machine learning. Most existing literature focuses on binary classification, but achieving fairness in regression tasks-such as insurance pricing or hiring score assessments-is equally important. Moreover, anti-discrimination laws also apply to continuous attributes, such as age, for which many existing methods are not applicable. In practice, multiple protected attributes can exist simultaneously; however, methods targeting fairness across several attributes often overlook so-called "fairness gerrymandering", thereby ignoring disparities among intersectional subgroups (e.g., African-American women or Hispanic men). In this paper, we propose a distance covariance regularisation framework that mitigates the association between model predictions and protected attributes, in line with the fairness definition of demographic parity, and that captures both linear and nonlinear dependencies. To enhance applicability in the presence of multiple protected attributes, we extend our framework by incorporating two multivariate dependence measures based on distance covariance: the previously proposed joint distance covariance (JdCov) and our novel concatenated distance covariance (CCdCov), which effectively address fairness gerrymandering in both regression and classification tasks involving protected attributes of various types. We discuss and illustrate how to calibrate regularisation strength, including a method based on Jensen-Shannon divergence, which quantifies dissimilarities in prediction distributions across groups. We apply our framework to the COMPAS recidivism dataset and a large motor insurance claims dataset.

Distributional Refinement Network: Distributional Forecasting via Deep Learning

A key task in actuarial modelling involves modelling the distributional properties of losses. Classic (distributional) regression approaches like Generalized Linear Models (GLMs; Nelder and Wedderburn, 1972) are commonly used, but challenges remain in developing models that can (i) allow covariates to flexibly impact different aspects of the conditional distribution, (ii) integrate developments in machine learning and AI to maximise the predictive power while considering (i), and, (iii) maintain a level of interpretability in the model to enhance trust in the model and its outputs, which is often compromised in efforts pursuing (i) and (ii). We tackle this problem by proposing a Distributional Refinement Network (DRN), which combines an inherently interpretable baseline model (such as GLMs) with a flexible neural network-a modified Deep Distribution Regression (DDR; Li et al., 2019) method. Inspired by the Combined Actuarial Neural Network (CANN; Schelldorfer and W{\''u}thrich, 2019), our approach flexibly refines the entire baseline distribution. As a result, the DRN captures varying effects of features across all quantiles, improving predictive performance while maintaining adequate interpretability. Using both synthetic and real-world data, we demonstrate the DRN's superior distributional forecasting capacity. The DRN has the potential to be a powerful distributional regression model in actuarial science and beyond.

Machine Learning with High-Cardinality Categorical Features in Actuarial Applications

High-cardinality categorical features are pervasive in actuarial data (e.g. occupation in commercial property insurance). Standard categorical encoding methods like one-hot encoding are inadequate in these settings. In this work, we present a novel _Generalised Linear Mixed Model Neural Network_ ("GLMMNet") approach to the modelling of high-cardinality categorical features. The GLMMNet integrates a generalised linear mixed model in a deep learning framework, offering the predictive power of neural networks and the transparency of random effects estimates, the latter of which cannot be obtained from the entity embedding models. Further, its flexibility to deal with any distribution in the exponential dispersion (ED) family makes it widely applicable to many actuarial contexts and beyond. We illustrate and compare the GLMMNet against existing approaches in a range of simulation experiments as well as in a real-life insurance case study. Notably, we find that the GLMMNet often outperforms or at least performs comparably with an entity embedded neural network, while providing the additional benefit of transparency, which is particularly valuable in practical applications. Importantly, while our model was motivated by actuarial applications, it can have wider applicability. The GLMMNet would suit any applications that involve high-cardinality categorical variables and where the response cannot be sufficiently modelled by a Gaussian distribution.