Integral Probability Metrics PAC-Bayes Bounds

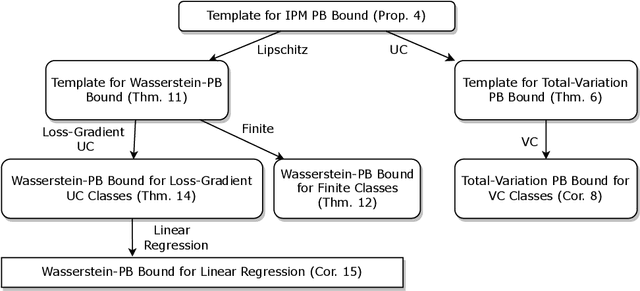
We present a PAC-Bayes-style generalization bound which enables the replacement of the KL-divergence with a variety of Integral Probability Metrics (IPM). We provide instances of this bound with the IPM being the total variation metric and the Wasserstein distance. A notable feature of the obtained bounds is that they naturally interpolate between classical uniform convergence bounds in the worst case (when the prior and posterior are far away from each other), and preferable bounds in better cases (when the posterior and prior are close). This illustrates the possibility of reinforcing classical generalization bounds with algorithm- and data-dependent components, thus making them more suitable to analyze algorithms that use a large hypothesis space.

Generalization Bounds For Unsupervised and Semi-Supervised Learning With Autoencoders

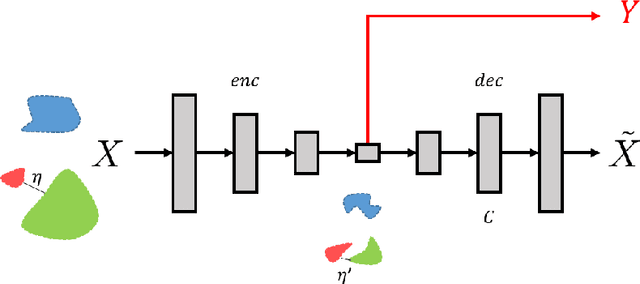
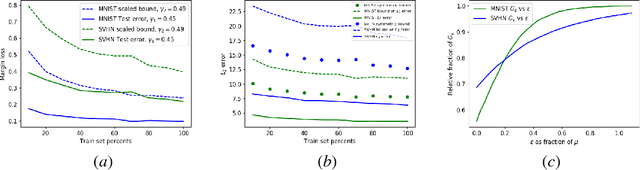
Autoencoders are widely used for unsupervised learning and as a regularization scheme in semi-supervised learning. However, theoretical understanding of their generalization properties and of the manner in which they can assist supervised learning has been lacking. We utilize recent advances in the theory of deep learning generalization, together with a novel reconstruction loss, to provide generalization bounds for autoencoders. To the best of our knowledge, this is the first such bound. We further show that, under appropriate assumptions, an autoencoder with good generalization properties can improve any semi-supervised learning scheme. We support our theoretical results with empirical demonstrations.