Change of Thought: Adaptive Test-Time Computation

Transformers evaluated in a single, fixed-depth pass are provably limited in expressive power to the constant-depth circuit class TC0. Running a Transformer autoregressively removes that ceiling -- first in next-token prediction and, more recently, in chain-of-thought reasoning. Both regimes rely on feedback loops that decode internal states into tokens only to re-encode them in subsequent steps. While this "thinking aloud" mirrors human reasoning, biological brains iterate without externalising intermediate states as language. To boost the expressive power of encoder Transformers without resorting to token-level autoregression, we introduce the SELF-Transformer: an encoder layer that iteratively refines its own attention weights to a fixed point. Instead of producing -- in one pass -- the alignment matrix that remixes the input sequence, the SELF-Transformer iteratively updates that matrix internally, scaling test-time computation with input difficulty. This adaptivity yields up to 20\% accuracy gains on encoder-style benchmarks without increasing parameter count, demonstrating that input-adaptive alignment at test time offers substantial benefits for only a modest extra compute budget. Self-Transformers thus recover much of the expressive power of iterative reasoning while preserving the simplicity of pure encoder architectures.

Efficient Distributed Auto-Differentiation

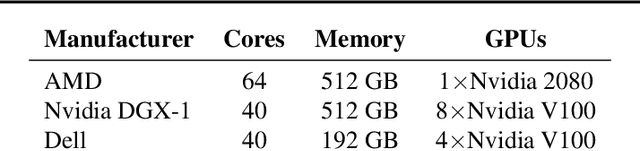
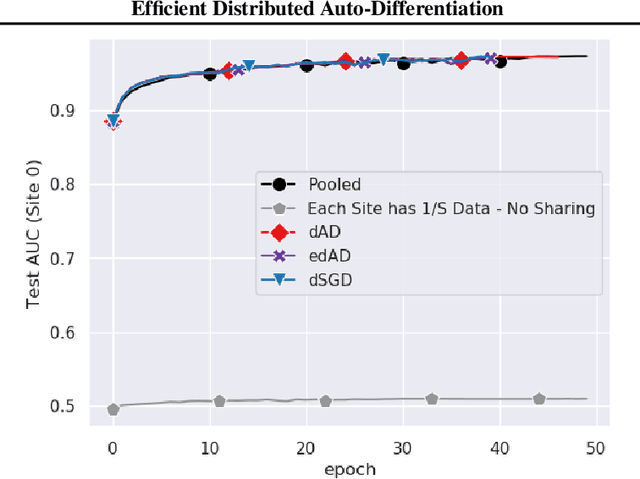
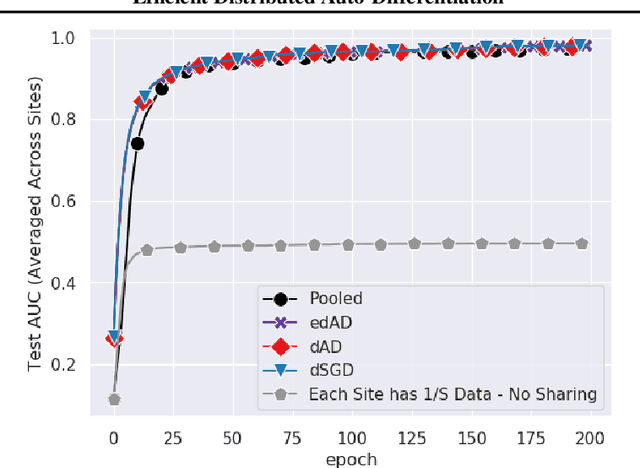
Although distributed machine learning has opened up numerous frontiers of research, the separation of large models across different devices, nodes, and sites can invite significant communication overhead, making reliable training difficult. The focus on gradients as the primary shared statistic during training has led to a number of intuitive algorithms for distributed deep learning; however, gradient-based algorithms for training large deep neural networks (DNNs) are communication-heavy, often requiring additional modifications via sparsity constraints, compression, quantization, and other similar approaches, to lower bandwidth. We introduce a surprisingly simple statistic for training distributed DNNs that is more communication-friendly than the gradient. The error backpropagation process can be modified to share these smaller intermediate values instead of the gradient, reducing communication overhead with no impact on accuracy. The process provides the flexibility of averaging gradients during backpropagation, enabling novel flexible training schemas while leaving room for further bandwidth reduction via existing gradient compression methods. Finally, consideration of the matrices used to compute the gradient inspires a new approach to compression via structured power iterations, which can not only reduce bandwidth but also enable introspection into distributed training dynamics, without significant performance loss.