Adaptive Learning with Artificial Barriers Yielding Nash Equilibria in General Games

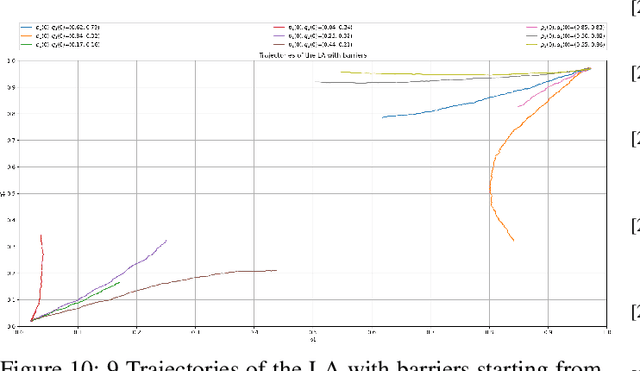
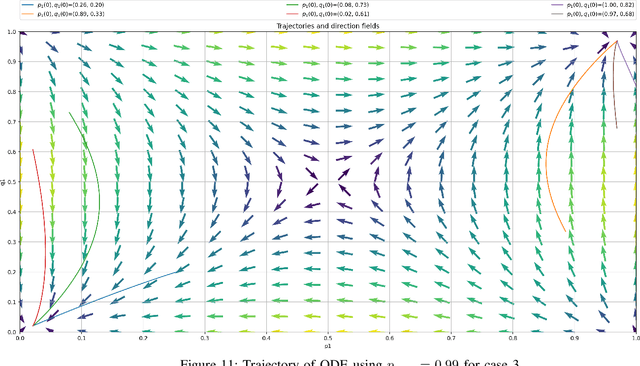
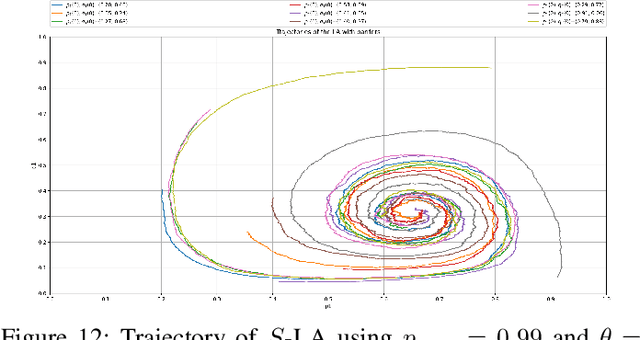
Artificial barriers in Learning Automata (LA) is a powerful and yet under-explored concept although it was first proposed in the 1980s. Introducing artificial non-absorbing barriers makes the LA schemes resilient to being trapped in absorbing barriers, a phenomenon which is often referred to as lock in probability leading to an exclusive choice of one action after convergence. Within the field of LA and reinforcement learning in general, there is a sacristy of theoretical works and applications of schemes with artificial barriers. In this paper, we devise a LA with artificial barriers for solving a general form of stochastic bimatrix game. Classical LA systems possess properties of absorbing barriers and they are a powerful tool in game theory and were shown to converge to game's of Nash equilibrium under limited information. However, the stream of works in LA for solving game theoretical problems can merely solve the case where the Saddle Point of the game exists in a pure strategy and fail to reach mixed Nash equilibrium when no Saddle Point exists for a pure strategy. In this paper, by resorting to the powerful concept of artificial barriers, we suggest a LA that converges to an optimal mixed Nash equilibrium even though there may be no Saddle Point when a pure strategy is invoked. Our deployed scheme is of Linear Reward-Inaction ($L_{R-I}$) flavor which is originally an absorbing LA scheme, however, we render it non-absorbing by introducing artificial barriers in an elegant and natural manner, in the sense that that the well-known legacy $L_{R-I}$ scheme can be seen as an instance of our proposed algorithm for a particular choice of the barrier. Furthermore, we present an $S$ Learning version of our LA with absorbing barriers that is able to handle $S$-Learning environment in which the feedback is continuous and not binary as in the case of the $L_{R-I}$.

Self Organizing Maps Whose Topologies Can Be Learned With Adaptive Binary Search Trees Using Conditional Rotations

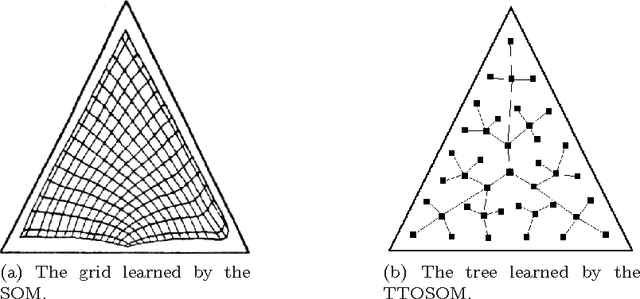
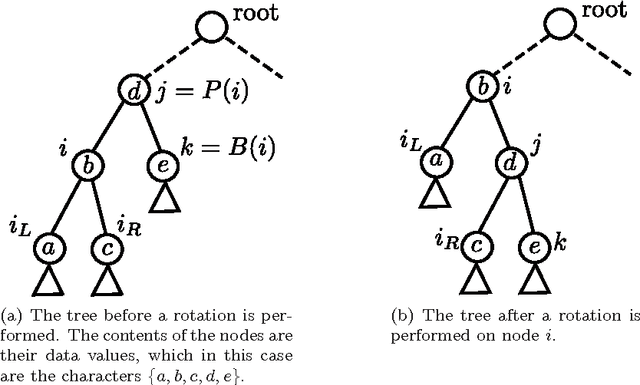
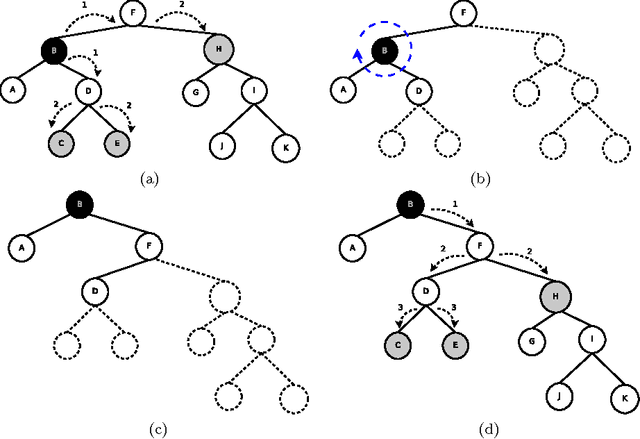
Numerous variants of Self-Organizing Maps (SOMs) have been proposed in the literature, including those which also possess an underlying structure, and in some cases, this structure itself can be defined by the user Although the concepts of growing the SOM and updating it have been studied, the whole issue of using a self-organizing Adaptive Data Structure (ADS) to further enhance the properties of the underlying SOM, has been unexplored. In an earlier work, we impose an arbitrary, user-defined, tree-like topology onto the codebooks, which consequently enforced a neighborhood phenomenon and the so-called tree-based Bubble of Activity. In this paper, we consider how the underlying tree itself can be rendered dynamic and adaptively transformed. To do this, we present methods by which a SOM with an underlying Binary Search Tree (BST) structure can be adaptively re-structured using Conditional Rotations (CONROT). These rotations on the nodes of the tree are local, can be done in constant time, and performed so as to decrease the Weighted Path Length (WPL) of the entire tree. In doing this, we introduce the pioneering concept referred to as Neural Promotion, where neurons gain prominence in the Neural Network (NN) as their significance increases. We are not aware of any research which deals with the issue of Neural Promotion. The advantages of such a scheme is that the user need not be aware of any of the topological peculiarities of the stochastic data distribution. Rather, the algorithm, referred to as the TTOSOM with Conditional Rotations (TTOCONROT), converges in such a manner that the neurons are ultimately placed in the input space so as to represent its stochastic distribution, and additionally, the neighborhood properties of the neurons suit the best BST that represents the data. These properties have been confirmed by our experimental results on a variety of data sets.