Towards Instance-Optimality in Online PAC Reinforcement Learning

Several recent works have proposed instance-dependent upper bounds on the number of episodes needed to identify, with probability $1-\delta$, an $\varepsilon$-optimal policy in finite-horizon tabular Markov Decision Processes (MDPs). These upper bounds feature various complexity measures for the MDP, which are defined based on different notions of sub-optimality gaps. However, as of now, no lower bound has been established to assess the optimality of any of these complexity measures, except for the special case of MDPs with deterministic transitions. In this paper, we propose the first instance-dependent lower bound on the sample complexity required for the PAC identification of a near-optimal policy in any tabular episodic MDP. Additionally, we demonstrate that the sample complexity of the PEDEL algorithm of \cite{Wagenmaker22linearMDP} closely approaches this lower bound. Considering the intractability of PEDEL, we formulate an open question regarding the possibility of achieving our lower bound using a computationally-efficient algorithm.

Active Coverage for PAC Reinforcement Learning

Collecting and leveraging data with good coverage properties plays a crucial role in different aspects of reinforcement learning (RL), including reward-free exploration and offline learning. However, the notion of "good coverage" really depends on the application at hand, as data suitable for one context may not be so for another. In this paper, we formalize the problem of active coverage in episodic Markov decision processes (MDPs), where the goal is to interact with the environment so as to fulfill given sampling requirements. This framework is sufficiently flexible to specify any desired coverage property, making it applicable to any problem that involves online exploration. Our main contribution is an instance-dependent lower bound on the sample complexity of active coverage and a simple game-theoretic algorithm, CovGame, that nearly matches it. We then show that CovGame can be used as a building block to solve different PAC RL tasks. In particular, we obtain a simple algorithm for PAC reward-free exploration with an instance-dependent sample complexity that, in certain MDPs which are "easy to explore", is lower than the minimax one. By further coupling this exploration algorithm with a new technique to do implicit eliminations in policy space, we obtain a computationally-efficient algorithm for best-policy identification whose instance-dependent sample complexity scales with gaps between policy values.

Optimistic PAC Reinforcement Learning: the Instance-Dependent View

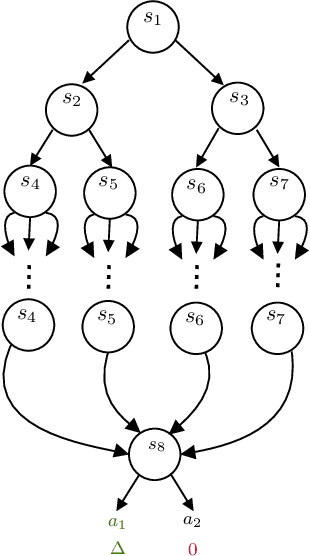
Optimistic algorithms have been extensively studied for regret minimization in episodic tabular MDPs, both from a minimax and an instance-dependent view. However, for the PAC RL problem, where the goal is to identify a near-optimal policy with high probability, little is known about their instance-dependent sample complexity. A negative result of Wagenmaker et al. (2021) suggests that optimistic sampling rules cannot be used to attain the (still elusive) optimal instance-dependent sample complexity. On the positive side, we provide the first instance-dependent bound for an optimistic algorithm for PAC RL, BPI-UCRL, for which only minimax guarantees were available (Kaufmann et al., 2021). While our bound features some minimal visitation probabilities, it also features a refined notion of sub-optimality gap compared to the value gaps that appear in prior work. Moreover, in MDPs with deterministic transitions, we show that BPI-UCRL is actually near-optimal. On the technical side, our analysis is very simple thanks to a new "target trick" of independent interest. We complement these findings with a novel hardness result explaining why the instance-dependent complexity of PAC RL cannot be easily related to that of regret minimization, unlike in the minimax regime.

Near Instance-Optimal PAC Reinforcement Learning for Deterministic MDPs

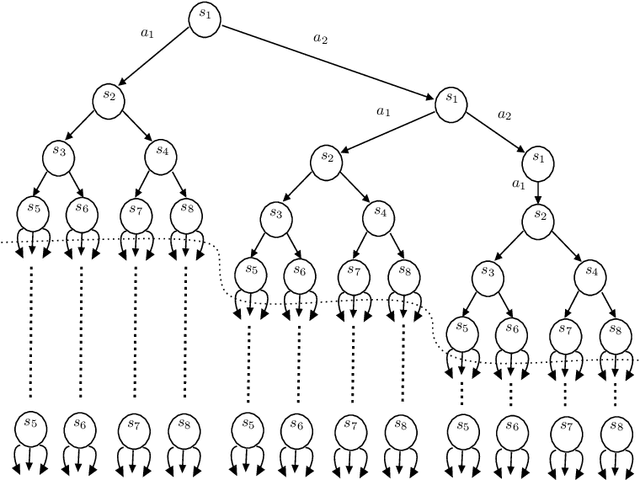
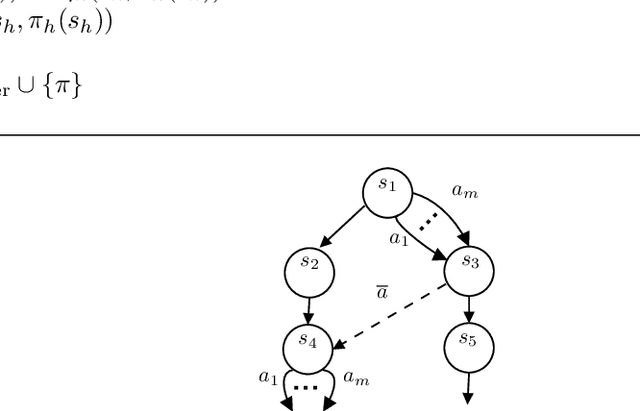
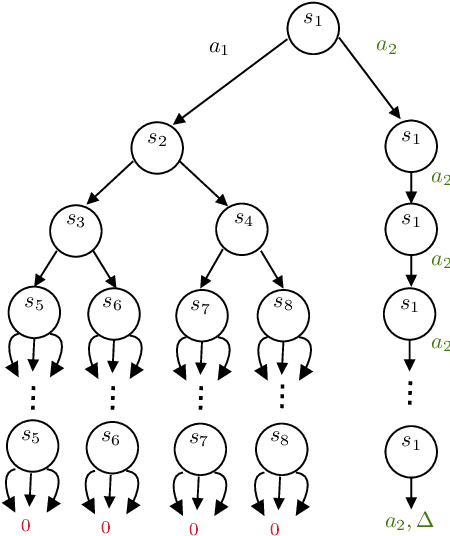
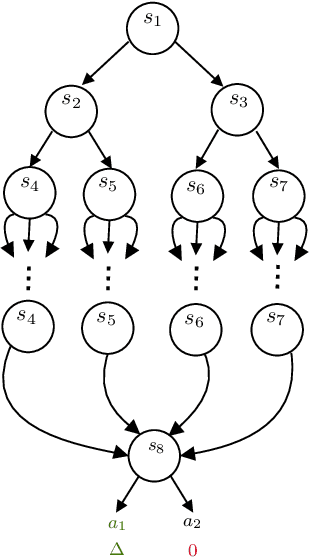
In probably approximately correct (PAC) reinforcement learning (RL), an agent is required to identify an $\epsilon$-optimal policy with probability $1-\delta$. While minimax optimal algorithms exist for this problem, its instance-dependent complexity remains elusive in episodic Markov decision processes (MDPs). In this paper, we propose the first (nearly) matching upper and lower bounds on the sample complexity of PAC RL in deterministic episodic MDPs with finite state and action spaces. In particular, our bounds feature a new notion of sub-optimality gap for state-action pairs that we call the deterministic return gap. While our instance-dependent lower bound is written as a linear program, our algorithms are very simple and do not require solving such an optimization problem during learning. Their design and analyses employ novel ideas, including graph-theoretical concepts such as minimum flows and maximum cuts, which we believe to shed new light on this problem.