Structural Explanations for Graph Neural Networks using HSIC

Graph neural networks (GNNs) are a type of neural model that tackle graphical tasks in an end-to-end manner. Recently, GNNs have been receiving increased attention in machine learning and data mining communities because of the higher performance they achieve in various tasks, including graph classification, link prediction, and recommendation. However, the complicated dynamics of GNNs make it difficult to understand which parts of the graph features contribute more strongly to the predictions. To handle the interpretability issues, recently, various GNN explanation methods have been proposed. In this study, a flexible model agnostic explanation method is proposed to detect significant structures in graphs using the Hilbert-Schmidt independence criterion (HSIC), which captures the nonlinear dependency between two variables through kernels. More specifically, we extend the GraphLIME method for node explanation with a group lasso and a fused lasso-based node explanation method. The group and fused regularization with GraphLIME enables the interpretation of GNNs in substructure units. Then, we show that the proposed approach can be used for the explanation of sequential graph classification tasks. Through experiments, it is demonstrated that our method can identify crucial structures in a target graph in various settings.

Computationally Efficient Wasserstein Loss for Structured Labels

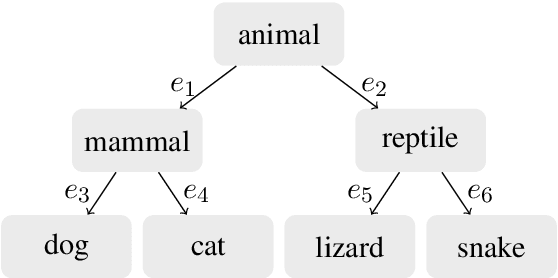
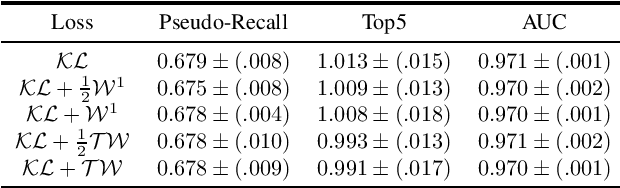
The problem of estimating the probability distribution of labels has been widely studied as a label distribution learning (LDL) problem, whose applications include age estimation, emotion analysis, and semantic segmentation. We propose a tree-Wasserstein distance regularized LDL algorithm, focusing on hierarchical text classification tasks. We propose predicting the entire label hierarchy using neural networks, where the similarity between predicted and true labels is measured using the tree-Wasserstein distance. Through experiments using synthetic and real-world datasets, we demonstrate that the proposed method successfully considers the structure of labels during training, and it compares favorably with the Sinkhorn algorithm in terms of computation time and memory usage.