On the Usage of Gaussian Process for Efficient Data Valuation

In machine learning, knowing the impact of a given datum on model training is a fundamental task referred to as Data Valuation. Building on previous works from the literature, we have designed a novel canonical decomposition allowing practitioners to analyze any data valuation method as the combination of two parts: a utility function that captures characteristics from a given model and an aggregation procedure that merges such information. We also propose to use Gaussian Processes as a means to easily access the utility function on ``sub-models'', which are models trained on a subset of the training set. The strength of our approach stems from both its theoretical grounding in Bayesian theory, and its practical reach, by enabling fast estimation of valuations thanks to efficient update formulae.

CRPS-Based Targeted Sequential Design with Application in Chemical Space

Sequential design of real and computer experiments via Gaussian Process (GP) models has proven useful for parsimonious, goal-oriented data acquisition purposes. In this work, we focus on acquisition strategies for a GP model that needs to be accurate within a predefined range of the response of interest. Such an approach is useful in various fields including synthetic chemistry, where finding molecules with particular properties is essential for developing useful materials and effective medications. GP modeling and sequential design of experiments have been successfully applied to a plethora of domains, including molecule research. Our main contribution here is to use the threshold-weighted Continuous Ranked Probability Score (CRPS) as a basic building block for acquisition functions employed within sequential design. We study pointwise and integral criteria relying on two different weighting measures and benchmark them against competitors, demonstrating improved performance with respect to considered goals. The resulting acquisition strategies are applicable to a wide range of fields and pave the way to further developing sequential design relying on scoring rules.

Goal-oriented adaptive sampling under random field modelling of response probability distributions

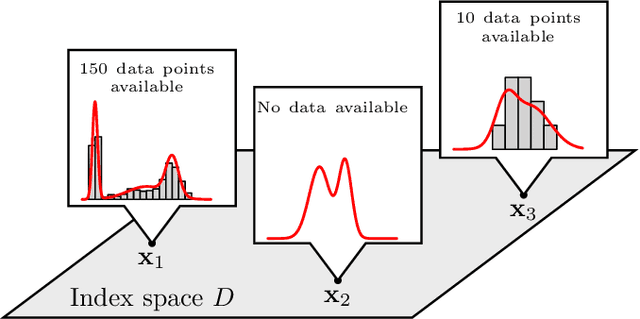
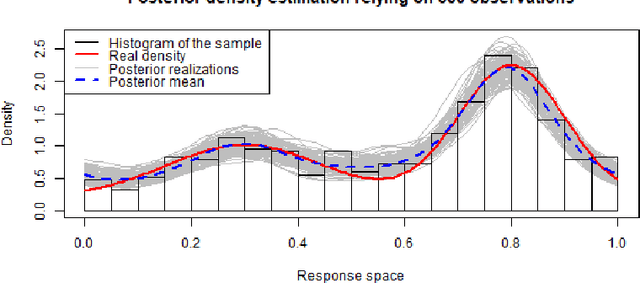
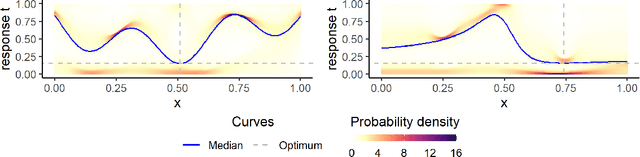
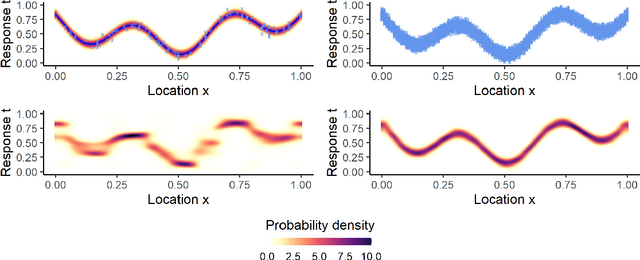
In the study of natural and artificial complex systems, responses that are not completely determined by the considered decision variables are commonly modelled probabilistically, resulting in response distributions varying across decision space. We consider cases where the spatial variation of these response distributions does not only concern their mean and/or variance but also other features including for instance shape or uni-modality versus multi-modality. Our contributions build upon a non-parametric Bayesian approach to modelling the thereby induced fields of probability distributions, and in particular to a spatial extension of the logistic Gaussian model. The considered models deliver probabilistic predictions of response distributions at candidate points, allowing for instance to perform (approximate) posterior simulations of probability density functions, to jointly predict multiple moments and other functionals of target distributions, as well as to quantify the impact of collecting new samples on the state of knowledge of the distribution field of interest. In particular, we introduce adaptive sampling strategies leveraging the potential of the considered random distribution field models to guide system evaluations in a goal-oriented way, with a view towards parsimoniously addressing calibration and related problems from non-linear (stochastic) inversion and global optimisation.