Synthetic aperture radar imaging below a random rough surface

Motivated by applications in unmanned aerial based ground penetrating radar for detecting buried landmines, we consider the problem of imaging small point like scatterers situated in a lossy medium below a random rough surface. Both the random rough surface and the absorption in the lossy medium significantly impede the target detection and imaging process. Using principal component analysis we effectively remove the reflection from the air-soil interface. We then use a modification of the classical synthetic aperture radar imaging functional to image the targets. This imaging method introduces a user-defined parameter, $\delta$, which scales the resolution by $\sqrt{\delta}$ allowing for target localization with sub wavelength accuracy. Numerical results in two dimensions illustrate the robustness of the approach for imaging multiple targets. However, the depth at which targets are detectable is limited due to the absorption in the lossy medium.

Synthetic aperture imaging of dispersive targets

We introduce a dispersive point target model based on scattering by a particle in the far-field. The synthetic aperture imaging problem is then expanded to identify these targets and recover their locations and frequency dependent reflectivities. We show that Kirchhoff migration (KM) is able to identify dispersive point targets in an imaging region. However, KM predicts target locations that are shifted in range from their true locations. We derive an estimate for this range shift for a single target. We also show that because of this range shift we cannot recover the complex-valued frequency dependent reflectivity, but we can recover its absolute value and hence the radar cross-section (RCS) of the target. Simulation results show that we can detect, recover the approximate location, and recover the RCS for dispersive point targets thereby opening opportunities to classifying important differences between multiple targets such as their sizes or material compositions.

Tunable high-resolution synthetic aperture radar imaging

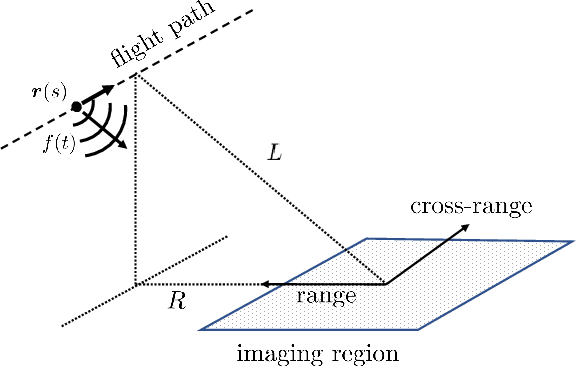
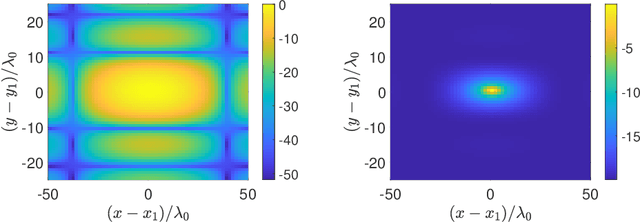
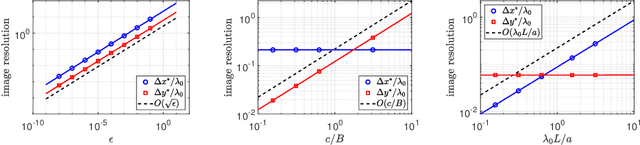
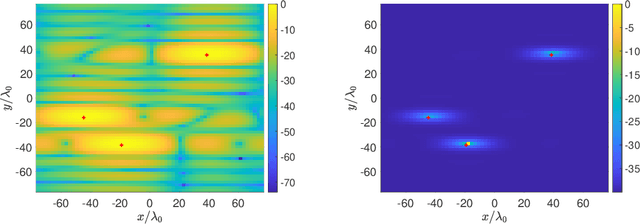
We have recently introduced a modification of the multiple signal classification (MUSIC) method for synthetic aperture radar. This method depends on a tunable, user-defined parameter, $\epsilon$, that allows for quantitative high-resolution imaging. It requires however, relative large single-to-noise ratios (SNR) to work effectively. Here, we first identify the fundamental mechanism in that method that produces high-resolution images. Then we introduce a modification to Kirchhoff Migration (KM) that uses the same mechanism to produces tunable, high-resolution images. This modified KM method can be applied to low SNR measurements. We show simulation results that demonstrate the features of this method.