Rank-One Modified Value Iteration

In this paper, we provide a novel algorithm for solving planning and learning problems of Markov decision processes. The proposed algorithm follows a policy iteration-type update by using a rank-one approximation of the transition probability matrix in the policy evaluation step. This rank-one approximation is closely related to the stationary distribution of the corresponding transition probability matrix, which is approximated using the power method. We provide theoretical guarantees for the convergence of the proposed algorithm to optimal (action-)value function with the same rate and computational complexity as the value iteration algorithm in the planning problem and as the Q-learning algorithm in the learning problem. Through our extensive numerical simulations, however, we show that the proposed algorithm consistently outperforms first-order algorithms and their accelerated versions for both planning and learning problems.

Adaptive Online Optimization with Predictions: Static and Dynamic Environments

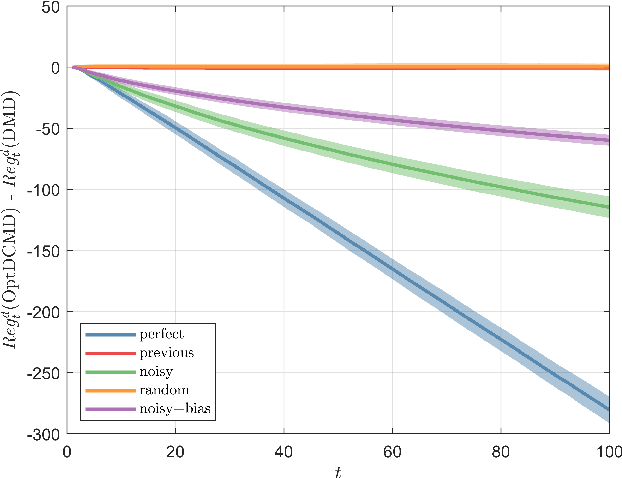
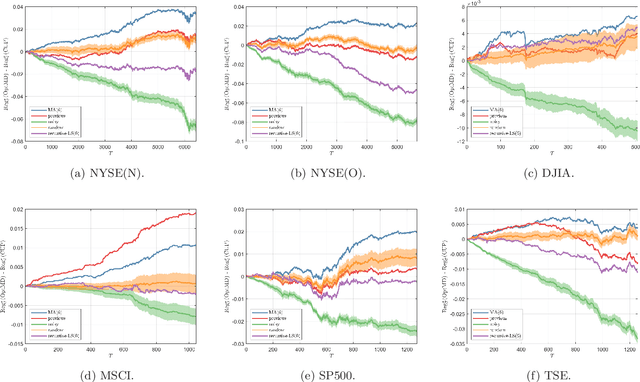
In the past few years, Online Convex Optimization (OCO) has received notable attention in the control literature thanks to its flexible real-time nature and powerful performance guarantees. In this paper, we propose new step-size rules and OCO algorithms that simultaneously exploit gradient predictions, function predictions and dynamics, features particularly pertinent to control applications. The proposed algorithms enjoy static and dynamic regret bounds in terms of the dynamics of the reference action sequence, gradient prediction error and function prediction error, which are generalizations of known regularity measures from the literature. We present results for both convex and strongly convex costs. We validate the performance of the proposed algorithms in a trajectory tracking case study, as well as portfolio optimization using real-world datasets.