Near-optimal Bayesian Solution For Unknown Discrete Markov Decision Process

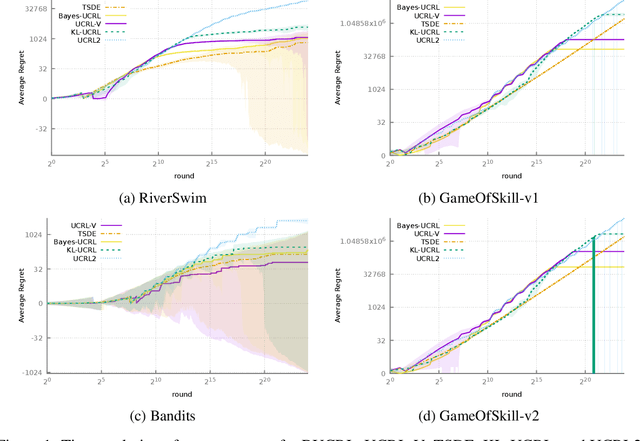
We tackle the problem of acting in an unknown finite and discrete Markov Decision Process (MDP) for which the expected shortest path from any state to any other state is bounded by a finite number $D$. An MDP consists of $S$ states and $A$ possible actions per state. Upon choosing an action $a_t$ at state $s_t$, one receives a real value reward $r_t$, then one transits to a next state $s_{t+1}$. The reward $r_t$ is generated from a fixed reward distribution depending only on $(s_t, a_t)$ and similarly, the next state $s_{t+1}$ is generated from a fixed transition distribution depending only on $(s_t, a_t)$. The objective is to maximize the accumulated rewards after $T$ interactions. In this paper, we consider the case where the reward distributions, the transitions, $T$ and $D$ are all unknown. We derive the first polynomial time Bayesian algorithm, BUCRL{} that achieves up to logarithm factors, a regret (i.e the difference between the accumulated rewards of the optimal policy and our algorithm) of the optimal order $\tilde{\mathcal{O}}(\sqrt{DSAT})$. Importantly, our result holds with high probability for the worst-case (frequentist) regret and not the weaker notion of Bayesian regret. We perform experiments in a variety of environments that demonstrate the superiority of our algorithm over previous techniques. Our work also illustrates several results that will be of independent interest. In particular, we derive a sharper upper bound for the KL-divergence of Bernoulli random variables. We also derive sharper upper and lower bounds for Beta and Binomial quantiles. All the bound are very simple and only use elementary functions.

Near-Optimal Online Egalitarian learning in General Sum Repeated Matrix Games

We study two-player general sum repeated finite games where the rewards of each player are generated from an unknown distribution. Our aim is to find the egalitarian bargaining solution (EBS) for the repeated game, which can lead to much higher rewards than the maximin value of both players. Our most important contribution is the derivation of an algorithm that achieves simultaneously, for both players, a high-probability regret bound of order $\mathcal{O}(\sqrt[3]{\ln T}\cdot T^{2/3})$ after any $T$ rounds of play. We demonstrate that our upper bound is nearly optimal by proving a lower bound of $\Omega(T^{2/3})$ for any algorithm.

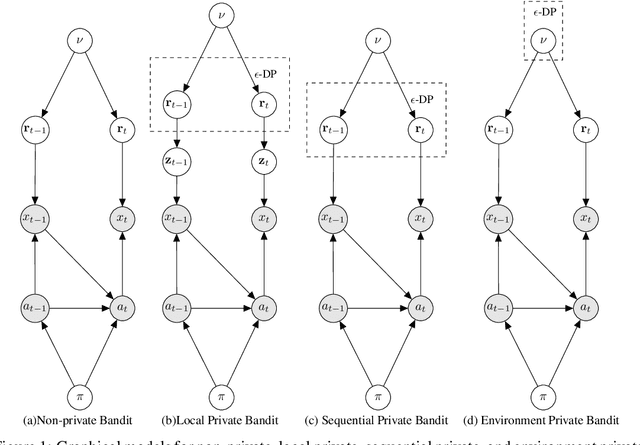
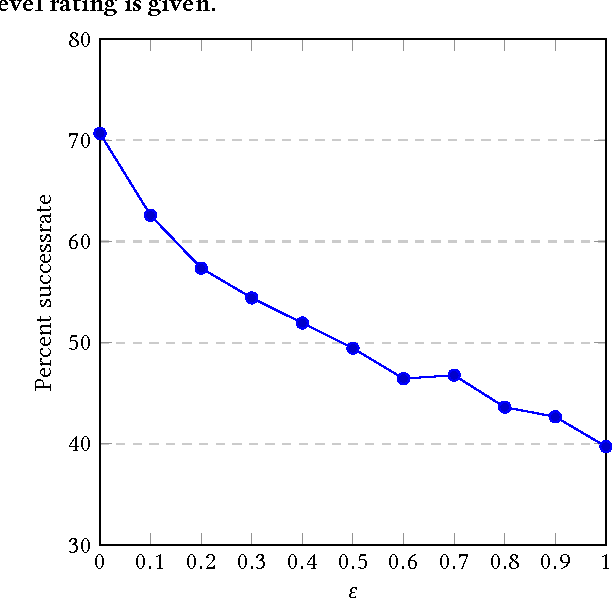
Differential Privacy for Multi-armed Bandits: What Is It and What Is Its Cost?

We introduce a number of privacy definitions for the multi-armed bandit problem, based on differential privacy. We relate them through a unifying graphical model representation and connect them to existing definitions. We then derive and contrast lower bounds on the regret of bandit algorithms satisfying these definitions. We show that for all of them, the learner's regret is increased by a multiplicative factor dependent on the privacy level $\epsilon$, but that the dependency is weaker when we do not require local differential privacy for the rewards.

Near-optimal Optimistic Reinforcement Learning using Empirical Bernstein Inequalities

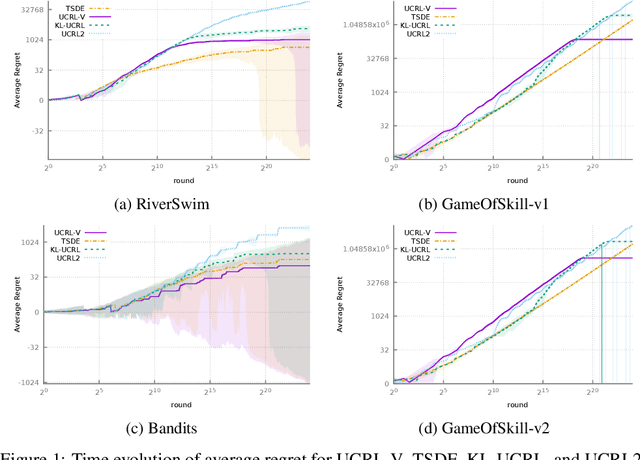
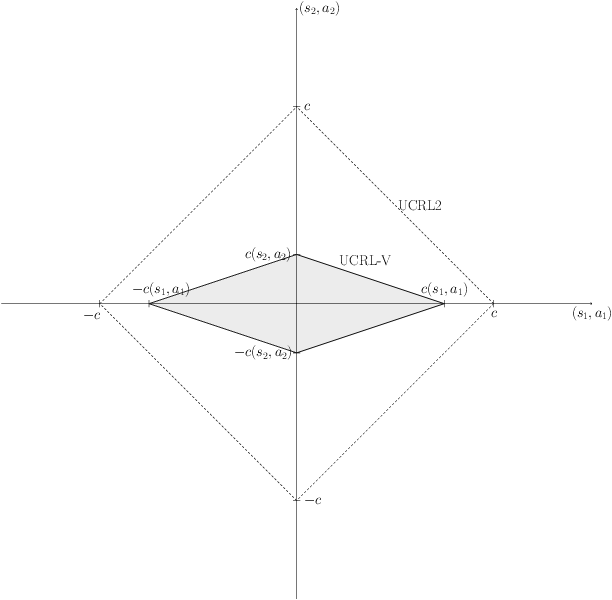
We study model-based reinforcement learning in an unknown finite communicating Markov decision process. We propose a simple algorithm that leverages a variance based confidence interval. We show that the proposed algorithm, UCRL-V, achieves the optimal regret $\tilde{\mathcal{O}}(\sqrt{DSAT})$ up to logarithmic factors, and so our work closes a gap with the lower bound without additional assumptions on the MDP. We perform experiments in a variety of environments that validates the theoretical bounds as well as prove UCRL-V to be better than the state-of-the-art algorithms.

Learning to Match

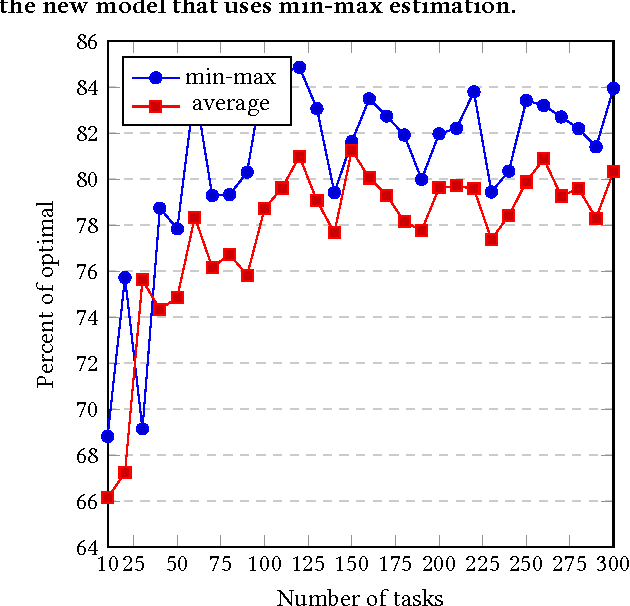
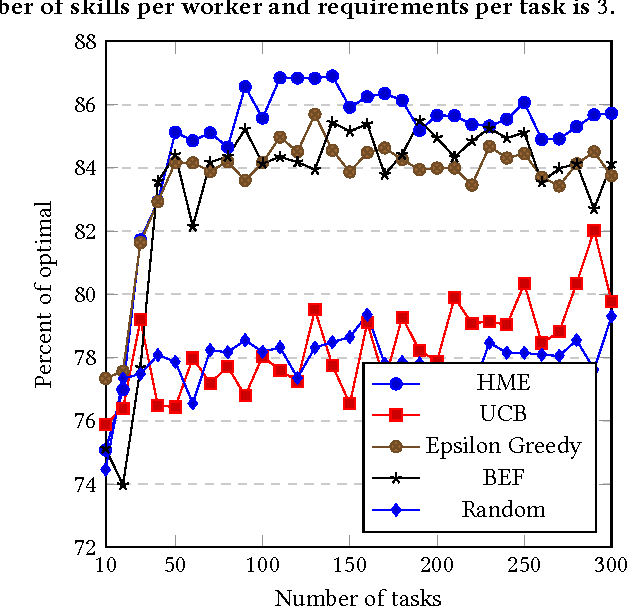
Outsourcing tasks to previously unknown parties is becoming more common. One specific such problem involves matching a set of workers to a set of tasks. Even if the latter have precise requirements, the quality of individual workers is usually unknown. The problem is thus a version of matching under uncertainty. We believe that this type of problem is going to be increasingly important. When the problem involves only a single skill or type of job, it is essentially a type of bandit problem, and can be solved with standard algorithms. However, we develop an algorithm that can perform matching for workers with multiple skills hired for multiple jobs with multiple requirements. We perform an experimental evaluation in both single-task and multi-task problems, comparing with the bounded $\epsilon$-first algorithm, as well as an oracle that knows the true skills of workers. One of the algorithms we developed gives results approaching 85\% of oracle's performance. We invite the community to take a closer look at this problem and develop real-world benchmarks.

Algorithms for Differentially Private Multi-Armed Bandits

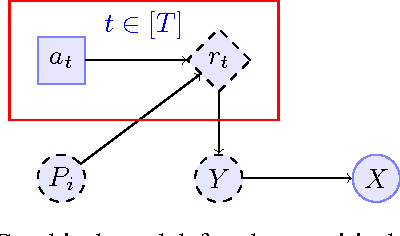
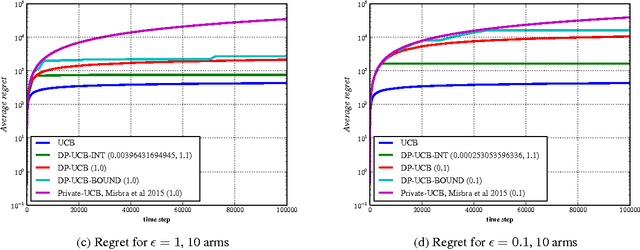
We present differentially private algorithms for the stochastic Multi-Armed Bandit (MAB) problem. This is a problem for applications such as adaptive clinical trials, experiment design, and user-targeted advertising where private information is connected to individual rewards. Our major contribution is to show that there exist $(\epsilon, \delta)$ differentially private variants of Upper Confidence Bound algorithms which have optimal regret, $O(\epsilon^{-1} + \log T)$. This is a significant improvement over previous results, which only achieve poly-log regret $O(\epsilon^{-2} \log^{2} T)$, because of our use of a novel interval-based mechanism. We also substantially improve the bounds of previous family of algorithms which use a continual release mechanism. Experiments clearly validate our theoretical bounds.

Probabilistic inverse reinforcement learning in unknown environments

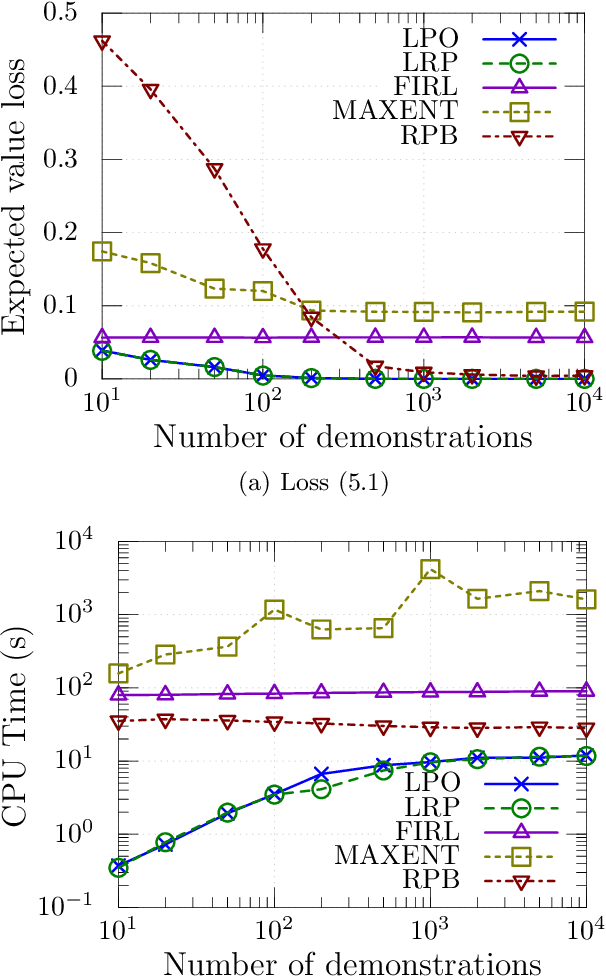
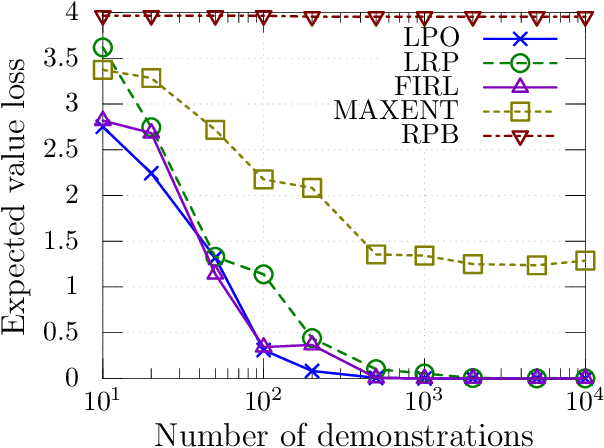
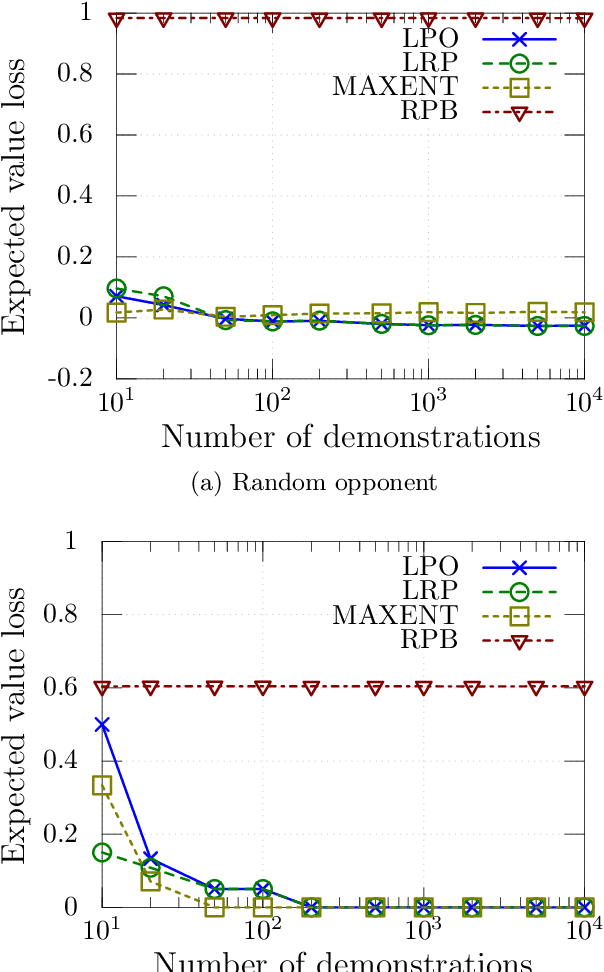
We consider the problem of learning by demonstration from agents acting in unknown stochastic Markov environments or games. Our aim is to estimate agent preferences in order to construct improved policies for the same task that the agents are trying to solve. To do so, we extend previous probabilistic approaches for inverse reinforcement learning in known MDPs to the case of unknown dynamics or opponents. We do this by deriving two simplified probabilistic models of the demonstrator's policy and utility. For tractability, we use maximum a posteriori estimation rather than full Bayesian inference. Under a flat prior, this results in a convex optimisation problem. We find that the resulting algorithms are highly competitive against a variety of other methods for inverse reinforcement learning that do have knowledge of the dynamics.