Deep learning and multi-level featurization of graph representations of microstructural data

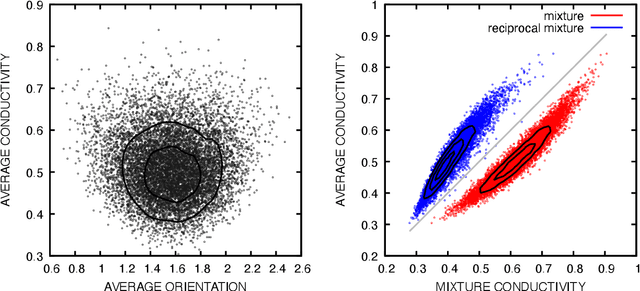
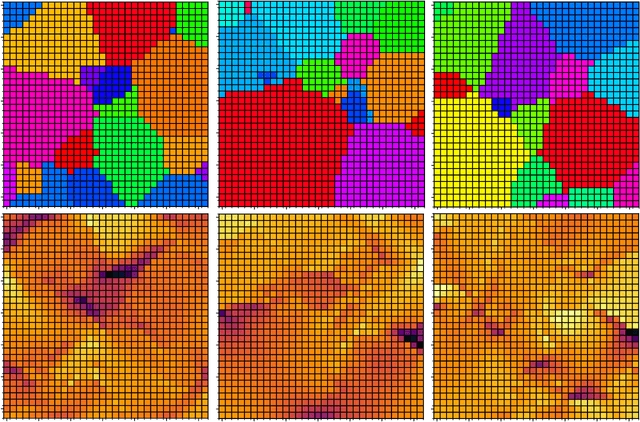
Many material response functions depend strongly on microstructure, such as inhomogeneities in phase or orientation. Homogenization presents the task of predicting the mean response of a sample of the microstructure to external loading for use in subgrid models and structure-property explorations. Although many microstructural fields have obvious segmentations, learning directly from the graph induced by the segmentation can be difficult because this representation does not encode all the information of the full field. We develop a means of deep learning of hidden features on the reduced graph given the native discretization and a segmentation of the initial input field. The features are associated with regions represented as nodes on the reduced graph. This reduced representation is then the basis for the subsequent multi-level/scale graph convolutional network model. There are a number of advantages of reducing the graph before fully processing with convolutional layers it, such as interpretable features and efficiency on large meshes. We demonstrate the performance of the proposed network relative to convolutional neural networks operating directly on the native discretization of the data using three physical exemplars.

Gaussian Process Regression constrained by Boundary Value Problems

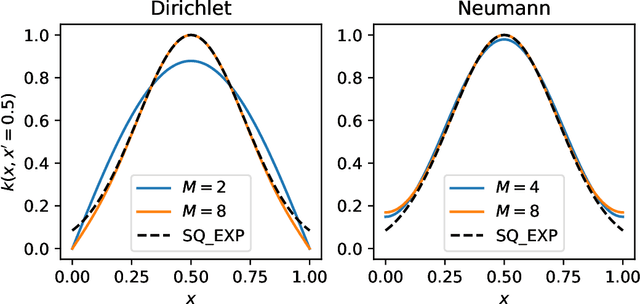
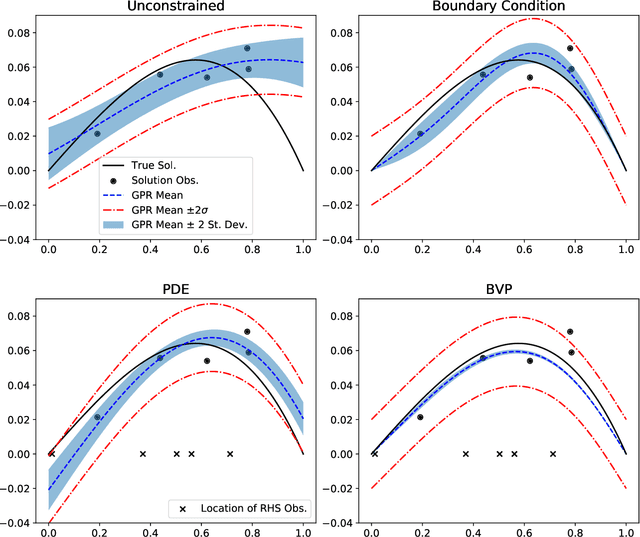
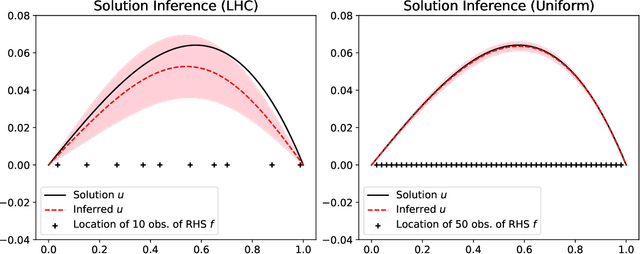
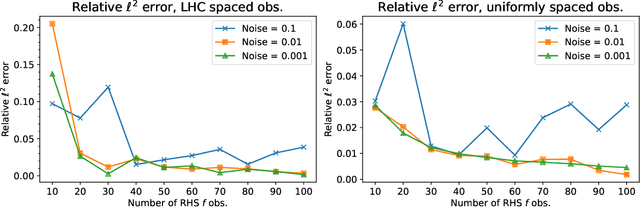
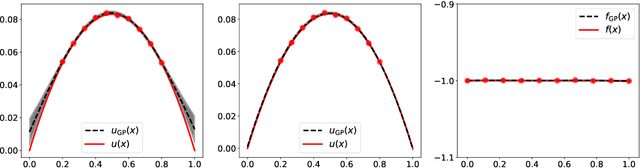
We develop a framework for Gaussian processes regression constrained by boundary value problems. The framework may be applied to infer the solution of a well-posed boundary value problem with a known second-order differential operator and boundary conditions, but for which only scattered observations of the source term are available. Scattered observations of the solution may also be used in the regression. The framework combines co-kriging with the linear transformation of a Gaussian process together with the use of kernels given by spectral expansions in eigenfunctions of the boundary value problem. Thus, it benefits from a reduced-rank property of covariance matrices. We demonstrate that the resulting framework yields more accurate and stable solution inference as compared to physics-informed Gaussian process regression without boundary condition constraints.

A Survey of Constrained Gaussian Process Regression: Approaches and Implementation Challenges

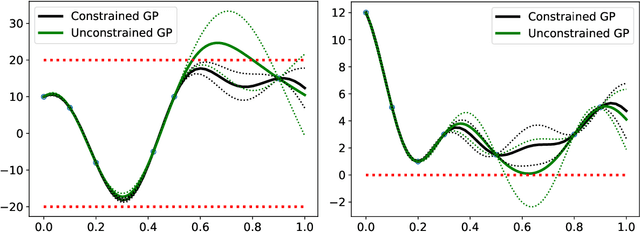
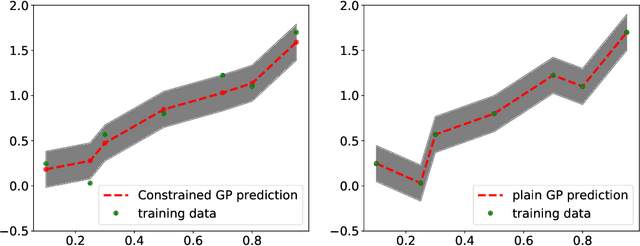
Gaussian process regression is a popular Bayesian framework for surrogate modeling of expensive data sources. As part of a broader effort in scientific machine learning, many recent works have incorporated physical constraints or other a priori information within Gaussian process regression to supplement limited data and regularize the behavior of the model. We provide an overview and survey of several classes of Gaussian process constraints, including positivity or bound constraints, monotonicity and convexity constraints, differential equation constraints provided by linear PDEs, and boundary condition constraints. We compare the strategies behind each approach as well as the differences in implementation, concluding with a discussion of the computational challenges introduced by constraints.

Tensor Basis Gaussian Process Models of Hyperelastic Materials

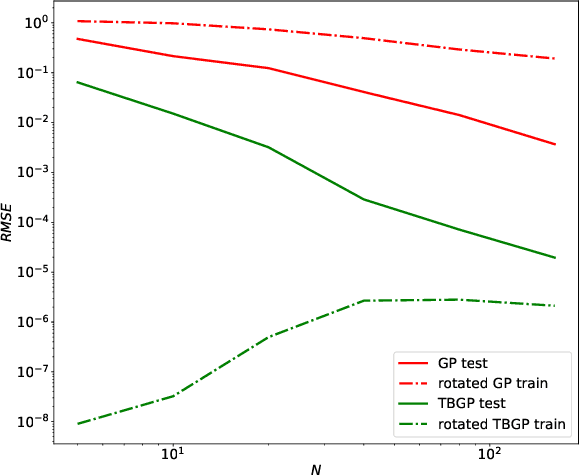
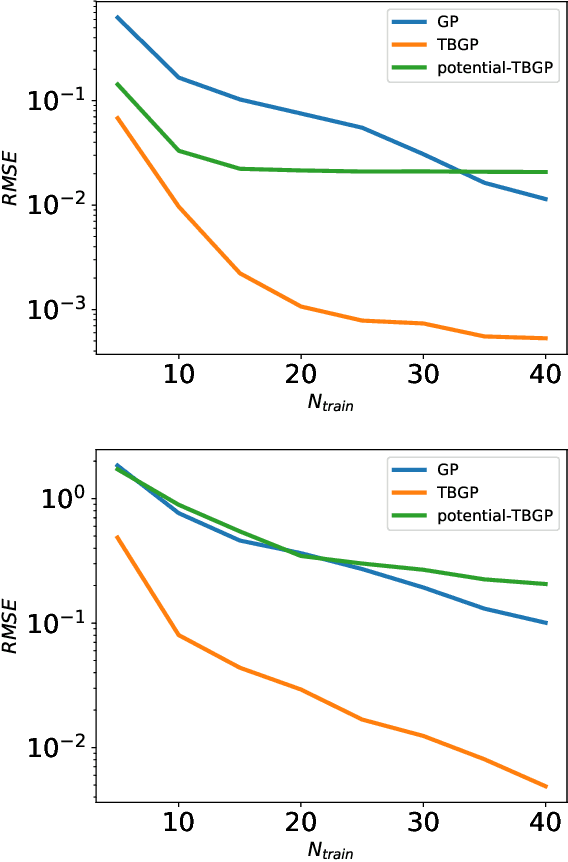
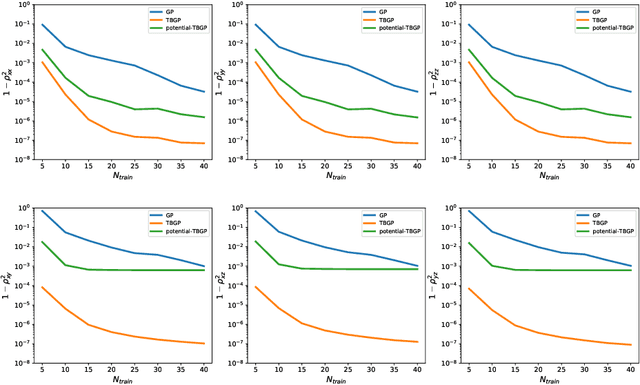
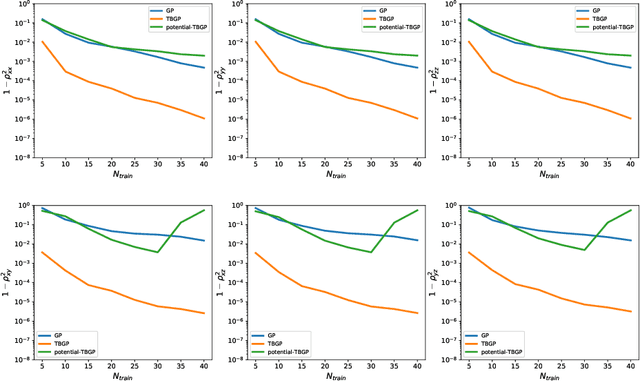
In this work, we develop Gaussian process regression (GPR) models of hyperelastic material behavior. First, we consider the direct approach of modeling the components of the Cauchy stress tensor as a function of the components of the Finger stretch tensor in a Gaussian process. We then consider an improvement on this approach that embeds rotational invariance of the stress-stretch constitutive relation in the GPR representation. This approach requires fewer training examples and achieves higher accuracy while maintaining invariance to rotations exactly. Finally, we consider an approach that recovers the strain-energy density function and derives the stress tensor from this potential. Although the error of this model for predicting the stress tensor is higher, the strain-energy density is recovered with high accuracy from limited training data. The approaches presented here are examples of physics-informed machine learning. They go beyond purely data-driven approaches by embedding the physical system constraints directly into the Gaussian process representation of materials models.