MM Algorithms to Estimate Parameters in Continuous-time Markov Chains

Continuous-time Markov chains (CTMCs) are popular modeling formalism that constitutes the underlying semantics for real-time probabilistic systems such as queuing networks, stochastic process algebras, and calculi for systems biology. Prism and Storm are popular model checking tools that provide a number of powerful analysis techniques for CTMCs. These tools accept models expressed as the parallel composition of a number of modules interacting with each other. The outcome of the analysis is strongly dependent on the parameter values used in the model which govern the timing and probability of events of the resulting CTMC. However, for some applications, parameter values have to be empirically estimated from partially-observable executions. In this work, we address the problem of estimating parameter values of CTMCs expressed as Prism models from a number of partially-observable executions. We introduce the class parametric CTMCs -- CTMCs where transition rates are polynomial functions over a set of parameters -- as an abstraction of CTMCs covering a large class of Prism models. Then, building on a theory of algorithms known by the initials MM, for minorization-maximization, we present iterative maximum likelihood estimation algorithms for parametric CTMCs covering two learning scenarios: when both state-labels and dwell times are observable, or just state-labels are. We conclude by illustrating the use of our technique in a simple but non-trivial case study: the analysis of the spread of COVID-19 in presence of lockdown countermeasures.

Active Learning of Markov Decision Processes using Baum-Welch algorithm (Extended)

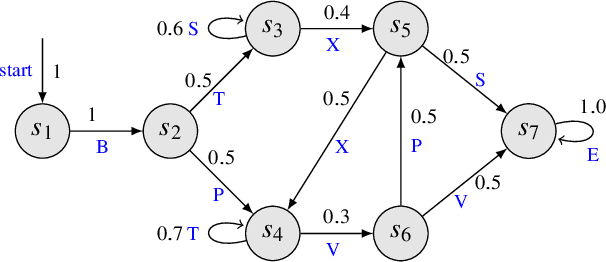
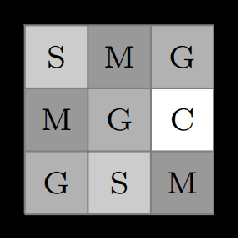
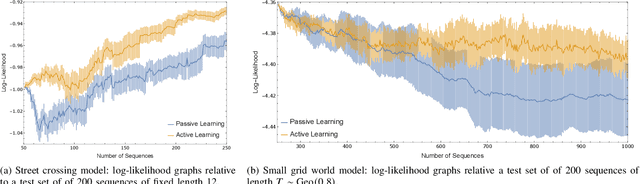
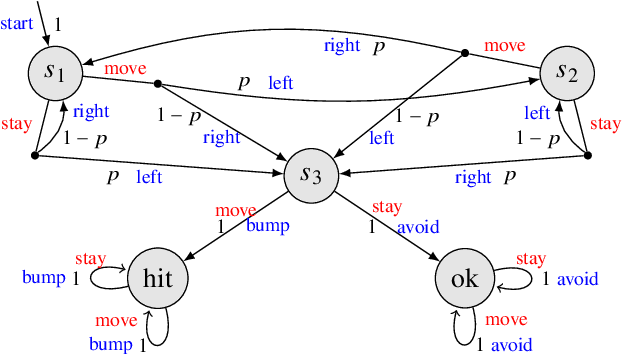
Cyber-physical systems (CPSs) are naturally modelled as reactive systems with nondeterministic and probabilistic dynamics. Model-based verification techniques have proved effective in the deployment of safety-critical CPSs. Central for a successful application of such techniques is the construction of an accurate formal model for the system. Manual construction can be a resource-demanding and error-prone process, thus motivating the design of automata learning algorithms to synthesise a system model from observed system behaviours. This paper revisits and adapts the classic Baum-Welch algorithm for learning Markov decision processes and Markov chains. For the case of MDPs, which typically demand more observations, we present a model-based active learning sampling strategy that choses examples which are most informative w.r.t.\ the current model hypothesis. We empirically compare our approach with state-of-the-art tools and demonstrate that the proposed active learning procedure can significantly reduce the number of observations required to obtain accurate models.