A Functional Model Method for Nonconvex Nonsmooth Conditional Stochastic Optimization

We consider stochastic optimization problems involving an expected value of a nonlinear function of a base random vector and a conditional expectation of another function depending on the base random vector, a dependent random vector, and the decision variables. We call such problems conditional stochastic optimization problems. They arise in many applications, such as uplift modeling, reinforcement learning, and contextual optimization. We propose a specialized single time-scale stochastic method for nonconvex constrained conditional stochastic optimization problems with a Lipschitz smooth outer function and a generalized differentiable inner function. In the method, we approximate the inner conditional expectation with a rich parametric model whose mean squared error satisfies a stochastic version of a {\L}ojasiewicz condition. The model is used by an inner learning algorithm. The main feature of our approach is that unbiased stochastic estimates of the directions used by the method can be generated with one observation from the joint distribution per iteration, which makes it applicable to real-time learning. The directions, however, are not gradients or subgradients of any overall objective function. We prove the convergence of the method with probability one, using the method of differential inclusions and a specially designed Lyapunov function, involving a stochastic generalization of the Bregman distance. Finally, a numerical illustration demonstrates the viability of our approach.

A Stochastic Subgradient Method for Distributionally Robust Non-Convex Learning

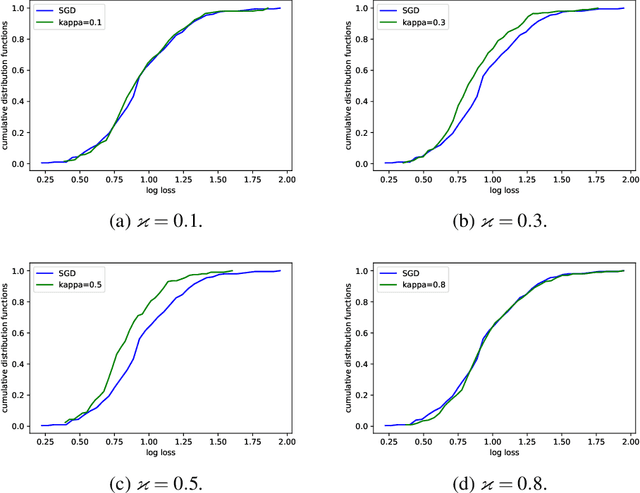
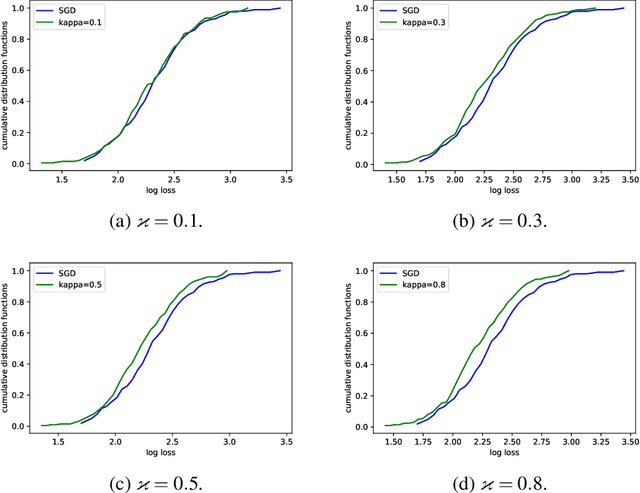
We consider a distributionally robust formulation of stochastic optimization problems arising in statistical learning, where robustness is with respect to uncertainty in the underlying data distribution. Our formulation builds on risk-averse optimization techniques and the theory of coherent risk measures. It uses semi-deviation risk for quantifying uncertainty, allowing us to compute solutions that are robust against perturbations in the population data distribution. We consider a large family of loss functions that can be non-convex and non-smooth and develop an efficient stochastic subgradient method. We prove that it converges to a point satisfying the optimality conditions. To our knowledge, this is the first method with rigorous convergence guarantees in the context of non-convex non-smooth distributionally robust stochastic optimization. Our method can achieve any desired level of robustness with little extra computational cost compared to population risk minimization. We also illustrate the performance of our algorithm on real datasets arising in convex and non-convex supervised learning problems.