Satisfiability and Synthesis Modulo Oracles

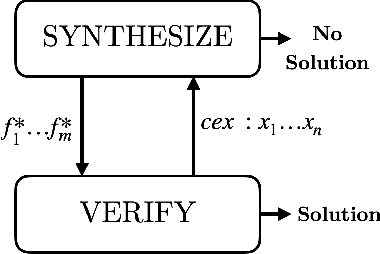
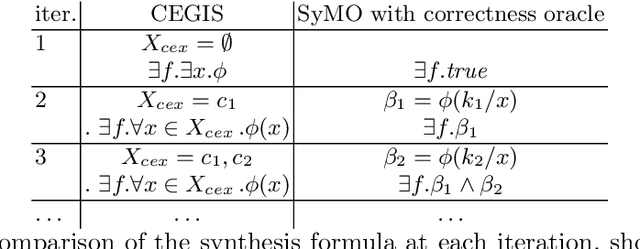
In classic program synthesis algorithms, such as counterexample-guided inductive synthesis (CEGIS), the algorithms alternate between a synthesis phase and an oracle (verification) phase. Many synthesis algorithms use a white-box oracle based on satisfiability modulo theory (SMT) solvers to provide counterexamples. But what if a white-box oracle is either not available or not easy to work with? We present a framework for solving a general class of oracle-guided synthesis problems which we term synthesis modulo oracles. In this setting, oracles may be black boxes with a query-response interface defined by the synthesis problem. As a necessary component of this framework, we also formalize the problem of satisfiability modulo theories and oracles, and present an algorithm for solving this problem. We implement a prototype solver for satisfiability and synthesis modulo oracles and demonstrate that, by using oracles that execute functions not easily modeled in SMT-constraints, such as recursive functions or oracles that incorporate compilation and execution of code, SMTO and SyMO are able to solve problems beyond the abilities of standard SMT and synthesis solvers.

Fair and Adventurous Enumeration of Quantifier Instantiations

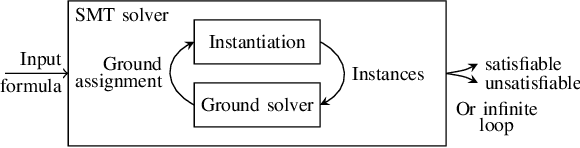
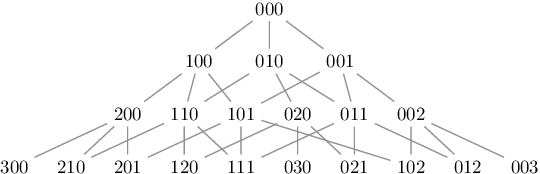
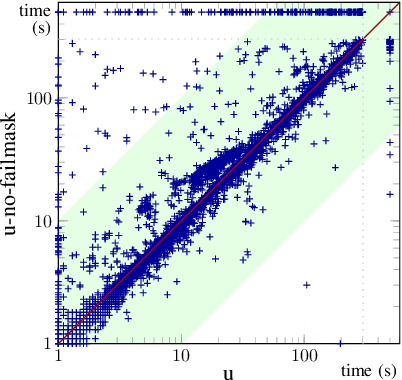
SMT solvers generally tackle quantifiers by instantiating their variables with tuples of terms from the ground part of the formula. Recent enumerative approaches for quantifier instantiation consider tuples of terms in some heuristic order. This paper studies different strategies to order such tuples and their impact on performance. We decouple the ordering problem into two parts. First is the order of the sequence of terms to consider for each quantified variable, and second is the order of the instantiation tuples themselves. While the most and least preferred tuples, i.e. those with all variables assigned to the most or least preferred terms, are clear, the combinations in between allow flexibility in an implementation. We look at principled strategies of complete enumeration, where some strategies are more fair, meaning they treat all the variables the same but some strategies may be more adventurous, meaning that they may venture further down the preference list. We further describe new techniques for discarding irrelevant instantiations which are crucial for the performance of these strategies in practice. These strategies are implemented in the SMT solver cvc5, where they contribute to the diversification of the solver's configuration space, as shown by our experimental results.