Superpixel-Based Image Segmentation Using Squared 2-Wasserstein Distances

We present an efficient method for image segmentation in the presence of strong inhomogeneities. The approach can be interpreted as a two-level clustering procedure: pixels are first grouped into superpixels via a linear least-squares assignment problem, which can be viewed as a special case of a discrete optimal transport (OT) problem, and these superpixels are subsequently greedily merged into object-level segments using the squared 2-Wasserstein distance between their empirical distributions. In contrast to conventional superpixel merging strategies based on mean-color distances, our framework employs a distributional OT distance, yielding a mathematically unified formulation across both clustering levels. Numerical experiments demonstrate that this perspective leads to improved segmentation accuracy on challenging images while retaining high computational efficiency.

Power-SLIC: Diagram-based superpixel generation

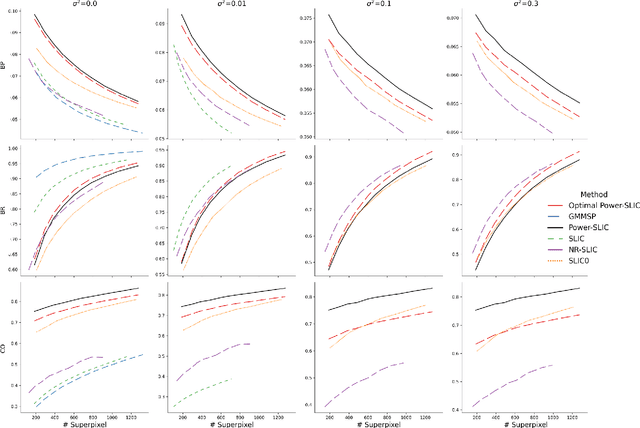
Superpixel algorithms, which group pixels similar in color and other low-level properties, are increasingly used for pre-processing in image segmentation. Commonly important criteria for the computation of superpixels are boundary adherence, speed, and regularity. Boundary adherence and regularity are typically contradictory goals. Most recent algorithms have focused on improving boundary adherence. Motivated by improving superpixel regularity, we propose a diagram-based superpixel generation method called Power-SLIC. On the BSDS500 data set, Power-SLIC outperforms other state-of-the-art algorithms in terms of compactness and boundary precision, and its boundary adherence is the most robust against varying levels of Gaussian noise. In terms of speed, Power-SLIC is competitive with SLIC.