Predicting Forced Responses of Probability Distributions via the Fluctuation-Dissipation Theorem and Generative Modeling

We present a novel data-driven framework for estimating the response of higher-order moments of nonlinear stochastic systems to small external perturbations. The classical Generalized Fluctuation-Dissipation Theorem (GFDT) links the unperturbed steady-state distribution to the system's linear response. Standard implementations rely on Gaussian approximations, which can often accurately predict the mean response but usually introduce significant biases in higher-order moments, such as variance, skewness, and kurtosis. To address this limitation, we combine GFDT with recent advances in score-based generative modeling, which enable direct estimation of the score function from data without requiring full density reconstruction. Our method is validated on three reduced-order stochastic models relevant to climate dynamics: a scalar stochastic model for low-frequency climate variability, a slow-fast triad model mimicking key features of the El Nino-Southern Oscillation (ENSO), and a six-dimensional stochastic barotropic model capturing atmospheric regime transitions. In all cases, the approach captures strongly nonlinear and non-Gaussian features of the system's response, outperforming traditional Gaussian approximations.

A Probabilistic Optimum-Path Forest Classifier for Binary Classification Problems

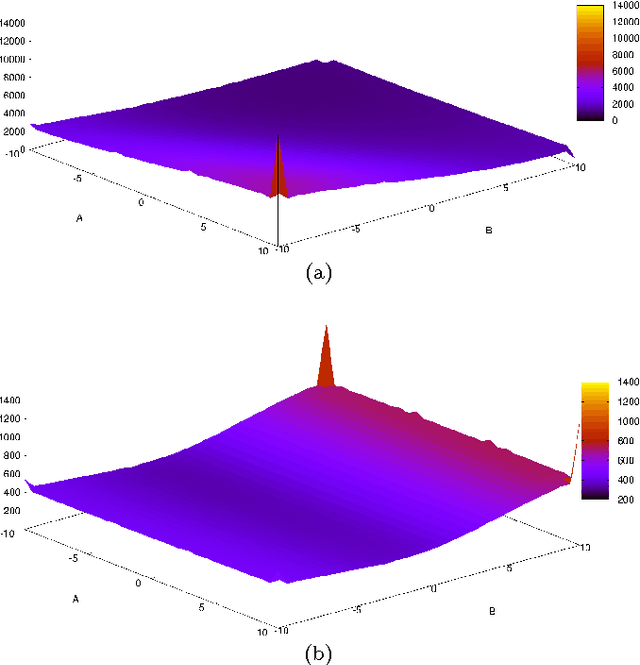
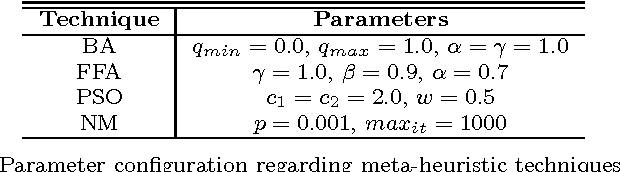
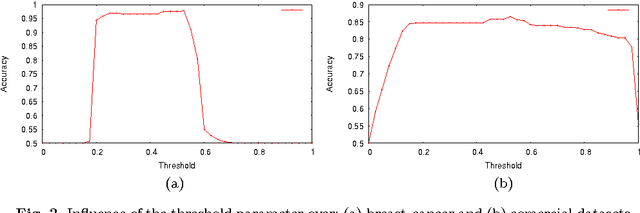
Probabilistic-driven classification techniques extend the role of traditional approaches that output labels (usually integer numbers) only. Such techniques are more fruitful when dealing with problems where one is not interested in recognition/identification only, but also into monitoring the behavior of consumers and/or machines, for instance. Therefore, by means of probability estimates, one can take decisions to work better in a number of scenarios. In this paper, we propose a probabilistic-based Optimum Path Forest (OPF) classifier to handle with binary classification problems, and we show it can be more accurate than naive OPF in a number of datasets. In addition to being just more accurate or not, probabilistic OPF turns to be another useful tool to the scientific community.