Incentivized Exploration via Filtered Posterior Sampling

We study "incentivized exploration" (IE) in social learning problems where the principal (a recommendation algorithm) can leverage information asymmetry to incentivize sequentially-arriving agents to take exploratory actions. We identify posterior sampling, an algorithmic approach that is well known in the multi-armed bandits literature, as a general-purpose solution for IE. In particular, we expand the existing scope of IE in several practically-relevant dimensions, from private agent types to informative recommendations to correlated Bayesian priors. We obtain a general analysis of posterior sampling in IE which allows us to subsume these extended settings as corollaries, while also recovering existing results as special cases.

Complexity Analysis of a Countable-armed Bandit Problem

We consider a stochastic multi-armed bandit (MAB) problem motivated by ``large'' action spaces, and endowed with a population of arms containing exactly $K$ arm-types, each characterized by a distinct mean reward. The decision maker is oblivious to the statistical properties of reward distributions as well as the population-level distribution of different arm-types, and is precluded also from observing the type of an arm after play. We study the classical problem of minimizing the expected cumulative regret over a horizon of play $n$, and propose algorithms that achieve a rate-optimal finite-time instance-dependent regret of $\mathcal{O}\left( \log n \right)$. We also show that the instance-independent (minimax) regret is $\tilde{\mathcal{O}}\left( \sqrt{n} \right)$ when $K=2$. While the order of regret and complexity of the problem suggests a great degree of similarity to the classical MAB problem, properties of the performance bounds and salient aspects of algorithm design are quite distinct from the latter, as are the key primitives that determine complexity along with the analysis tools needed to study them.

The Countable-armed Bandit with Vanishing Arms

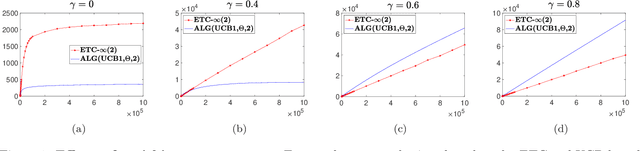
We consider a bandit problem with countably many arms, partitioned into finitely many "types," each characterized by a unique mean reward. A "non-stationary" distribution governs the relative abundance of each arm-type in the population of arms, aka the "arm-reservoir." This non-stationarity is attributable to a probabilistic leakage of "optimal" arms from the reservoir over time, which we refer to as the "vanishing arms" phenomenon; this induces a time-varying (potentially "endogenous," policy-dependent) distribution over the reservoir. The objective is minimization of the expected cumulative regret. We characterize necessary and sufficient conditions for achievability of sub-linear regret in terms of a critical vanishing rate of optimal arms. We also discuss two reservoir distribution-oblivious algorithms that are long-run-average optimal whenever sub-linear regret is statistically achievable. Numerical experiments highlight a distinctive characteristic of this problem related to ex ante knowledge of the "gap" parameter (the difference between the top two mean rewards): in contrast to the stationary bandit formulation, regret in our setting may suffer substantial inflation under adaptive exploration-based (gap-oblivious) algorithms such as UCB vis-`a-vis their non-adaptive forced exploration-based (gap-aware) counterparts like ETC.

A Closer Look at the Worst-case Behavior of Multi-armed Bandit Algorithms

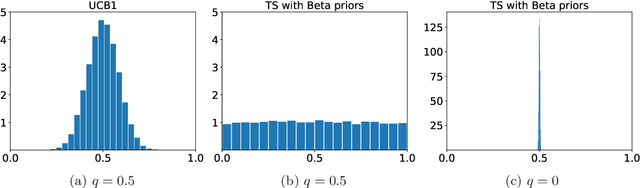
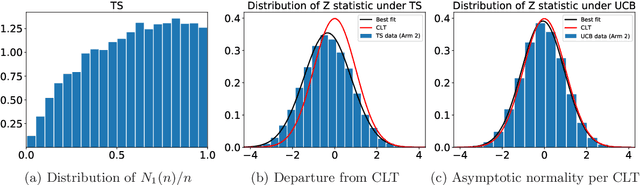
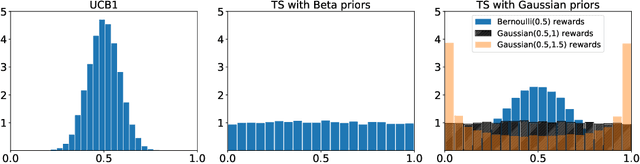
One of the key drivers of complexity in the classical (stochastic) multi-armed bandit (MAB) problem is the difference between mean rewards in the top two arms, also known as the instance gap. The celebrated Upper Confidence Bound (UCB) policy is among the simplest optimism-based MAB algorithms that naturally adapts to this gap: for a horizon of play n, it achieves optimal O(log n) regret in instances with "large" gaps, and a near-optimal O(\sqrt{n log n}) minimax regret when the gap can be arbitrarily "small." This paper provides new results on the arm-sampling behavior of UCB, leading to several important insights. Among these, it is shown that arm-sampling rates under UCB are asymptotically deterministic, regardless of the problem complexity. This discovery facilitates new sharp asymptotics and a novel alternative proof for the O(\sqrt{n log n}) minimax regret of UCB. Furthermore, the paper also provides the first complete process-level characterization of the MAB problem under UCB in the conventional diffusion scaling. Among other things, the "small" gap worst-case lens adopted in this paper also reveals profound distinctions between the behavior of UCB and Thompson Sampling, such as an "incomplete learning" phenomenon characteristic of the latter.

From Finite to Countable-Armed Bandits

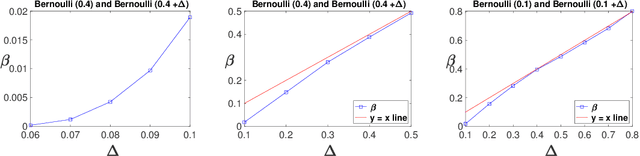
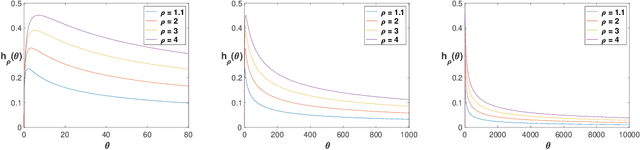
We consider a stochastic bandit problem with countably many arms that belong to a finite set of types, each characterized by a unique mean reward. In addition, there is a fixed distribution over types which sets the proportion of each type in the population of arms. The decision maker is oblivious to the type of any arm and to the aforementioned distribution over types, but perfectly knows the total number of types occurring in the population of arms. We propose a fully adaptive online learning algorithm that achieves O(log n) distribution-dependent expected cumulative regret after any number of plays n, and show that this order of regret is best possible. The analysis of our algorithm relies on newly discovered concentration and convergence properties of optimism-based policies like UCB in finite-armed bandit problems with "zero gap," which may be of independent interest.