Deep Learning and Quantum Entanglement: Fundamental Connections with Implications to Network Design

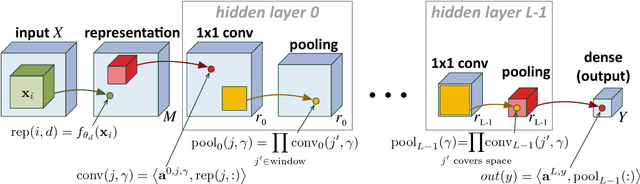
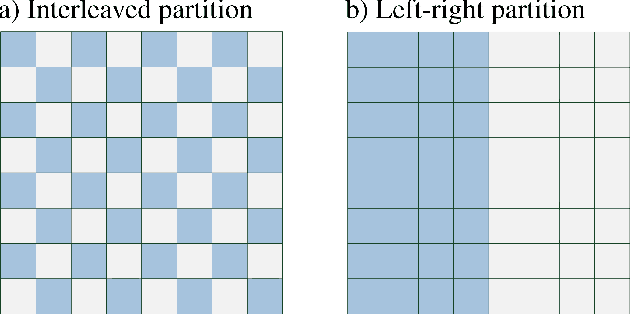
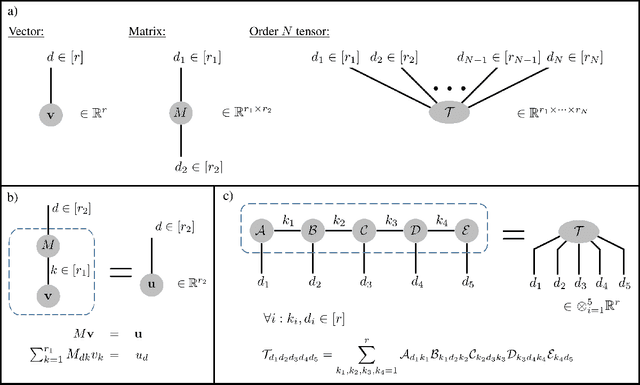
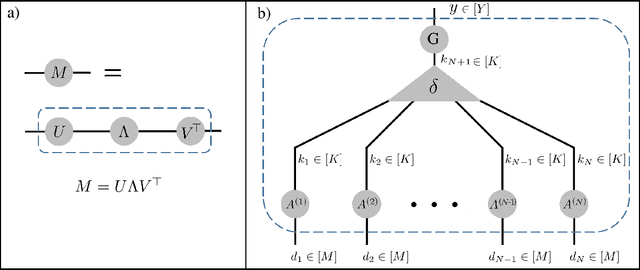
Deep convolutional networks have witnessed unprecedented success in various machine learning applications. Formal understanding on what makes these networks so successful is gradually unfolding, but for the most part there are still significant mysteries to unravel. The inductive bias, which reflects prior knowledge embedded in the network architecture, is one of them. In this work, we establish a fundamental connection between the fields of quantum physics and deep learning. We use this connection for asserting novel theoretical observations regarding the role that the number of channels in each layer of the convolutional network fulfills in the overall inductive bias. Specifically, we show an equivalence between the function realized by a deep convolutional arithmetic circuit (ConvAC) and a quantum many-body wave function, which relies on their common underlying tensorial structure. This facilitates the use of quantum entanglement measures as well-defined quantifiers of a deep network's expressive ability to model intricate correlation structures of its inputs. Most importantly, the construction of a deep ConvAC in terms of a Tensor Network is made available. This description enables us to carry a graph-theoretic analysis of a convolutional network, with which we demonstrate a direct control over the inductive bias of the deep network via its channel numbers, that are related to the min-cut in the underlying graph. This result is relevant to any practitioner designing a network for a specific task. We theoretically analyze ConvACs, and empirically validate our findings on more common ConvNets which involve ReLU activations and max pooling. Beyond the results described above, the description of a deep convolutional network in well-defined graph-theoretic tools and the formal connection to quantum entanglement, are two interdisciplinary bridges that are brought forth by this work.

Safe, Multi-Agent, Reinforcement Learning for Autonomous Driving

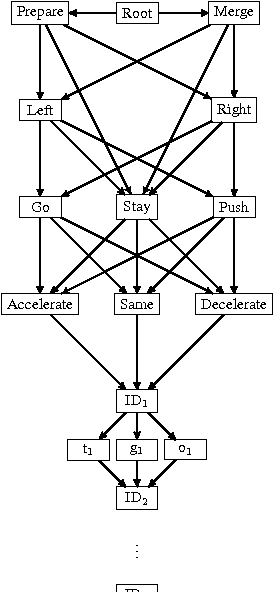
Autonomous driving is a multi-agent setting where the host vehicle must apply sophisticated negotiation skills with other road users when overtaking, giving way, merging, taking left and right turns and while pushing ahead in unstructured urban roadways. Since there are many possible scenarios, manually tackling all possible cases will likely yield a too simplistic policy. Moreover, one must balance between unexpected behavior of other drivers/pedestrians and at the same time not to be too defensive so that normal traffic flow is maintained. In this paper we apply deep reinforcement learning to the problem of forming long term driving strategies. We note that there are two major challenges that make autonomous driving different from other robotic tasks. First, is the necessity for ensuring functional safety - something that machine learning has difficulty with given that performance is optimized at the level of an expectation over many instances. Second, the Markov Decision Process model often used in robotics is problematic in our case because of unpredictable behavior of other agents in this multi-agent scenario. We make three contributions in our work. First, we show how policy gradient iterations can be used without Markovian assumptions. Second, we decompose the problem into a composition of a Policy for Desires (which is to be learned) and trajectory planning with hard constraints (which is not learned). The goal of Desires is to enable comfort of driving, while hard constraints guarantees the safety of driving. Third, we introduce a hierarchical temporal abstraction we call an "Option Graph" with a gating mechanism that significantly reduces the effective horizon and thereby reducing the variance of the gradient estimation even further.

On the Expressive Power of Deep Learning: A Tensor Analysis

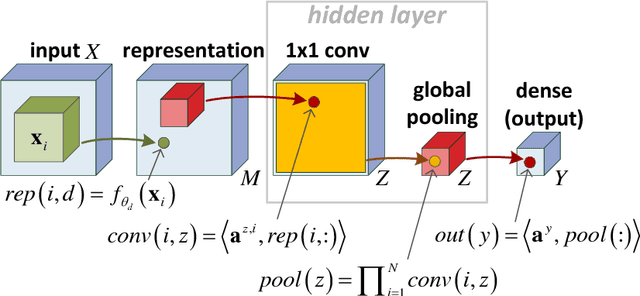
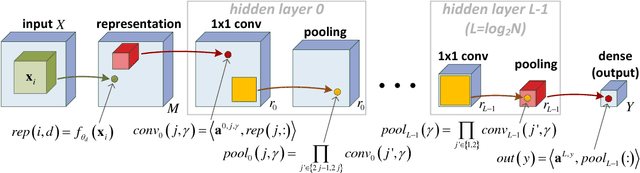
It has long been conjectured that hypotheses spaces suitable for data that is compositional in nature, such as text or images, may be more efficiently represented with deep hierarchical networks than with shallow ones. Despite the vast empirical evidence supporting this belief, theoretical justifications to date are limited. In particular, they do not account for the locality, sharing and pooling constructs of convolutional networks, the most successful deep learning architecture to date. In this work we derive a deep network architecture based on arithmetic circuits that inherently employs locality, sharing and pooling. An equivalence between the networks and hierarchical tensor factorizations is established. We show that a shallow network corresponds to CP (rank-1) decomposition, whereas a deep network corresponds to Hierarchical Tucker decomposition. Using tools from measure theory and matrix algebra, we prove that besides a negligible set, all functions that can be implemented by a deep network of polynomial size, require exponential size in order to be realized (or even approximated) by a shallow network. Since log-space computation transforms our networks into SimNets, the result applies directly to a deep learning architecture demonstrating promising empirical performance. The construction and theory developed in this paper shed new light on various practices and ideas employed by the deep learning community.

Learning a Metric Embedding for Face Recognition using the Multibatch Method

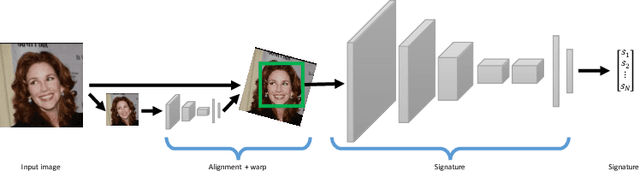
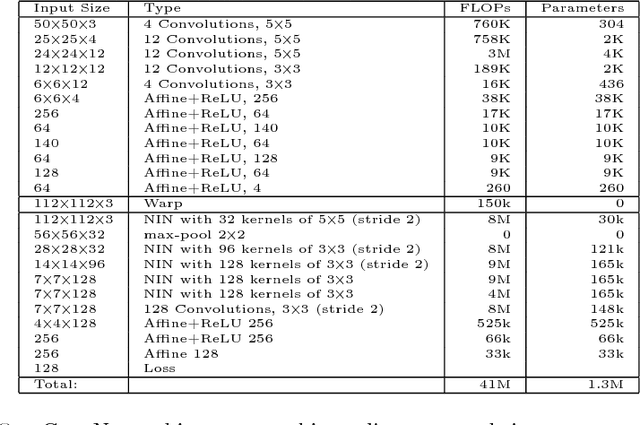
This work is motivated by the engineering task of achieving a near state-of-the-art face recognition on a minimal computing budget running on an embedded system. Our main technical contribution centers around a novel training method, called Multibatch, for similarity learning, i.e., for the task of generating an invariant "face signature" through training pairs of "same" and "not-same" face images. The Multibatch method first generates signatures for a mini-batch of $k$ face images and then constructs an unbiased estimate of the full gradient by relying on all $k^2-k$ pairs from the mini-batch. We prove that the variance of the Multibatch estimator is bounded by $O(1/k^2)$, under some mild conditions. In contrast, the standard gradient estimator that relies on random $k/2$ pairs has a variance of order $1/k$. The smaller variance of the Multibatch estimator significantly speeds up the convergence rate of stochastic gradient descent. Using the Multibatch method we train a deep convolutional neural network that achieves an accuracy of $98.2\%$ on the LFW benchmark, while its prediction runtime takes only $30$msec on a single ARM Cortex A9 core. Furthermore, the entire training process took only 12 hours on a single Titan X GPU.

Convolutional Rectifier Networks as Generalized Tensor Decompositions

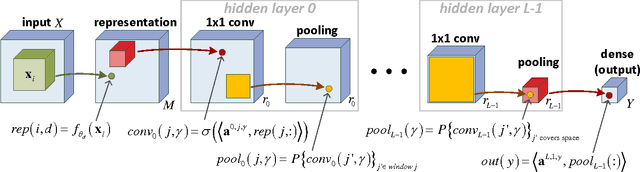
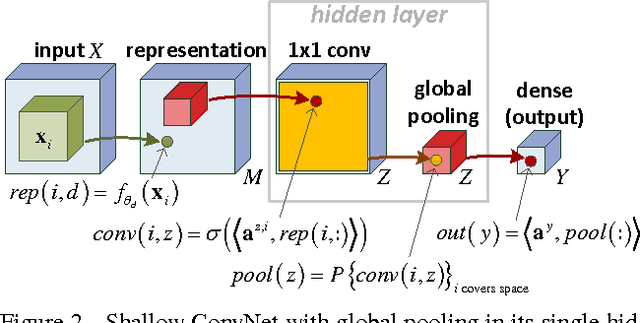
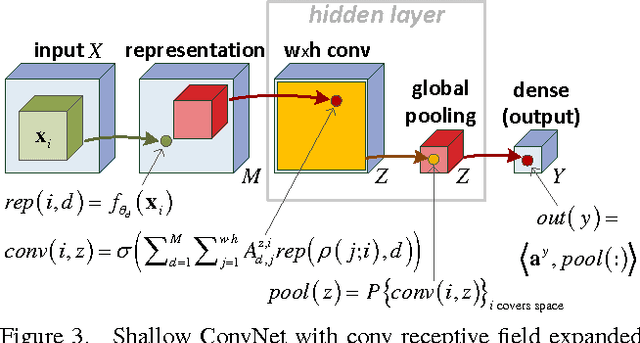
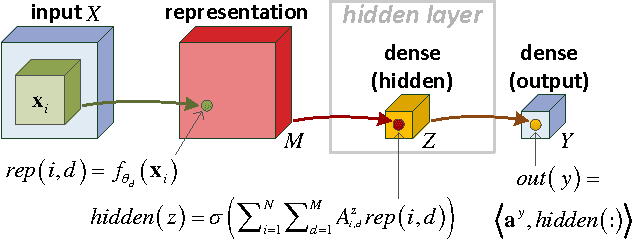
Convolutional rectifier networks, i.e. convolutional neural networks with rectified linear activation and max or average pooling, are the cornerstone of modern deep learning. However, despite their wide use and success, our theoretical understanding of the expressive properties that drive these networks is partial at best. On the other hand, we have a much firmer grasp of these issues in the world of arithmetic circuits. Specifically, it is known that convolutional arithmetic circuits possess the property of "complete depth efficiency", meaning that besides a negligible set, all functions that can be implemented by a deep network of polynomial size, require exponential size in order to be implemented (or even approximated) by a shallow network. In this paper we describe a construction based on generalized tensor decompositions, that transforms convolutional arithmetic circuits into convolutional rectifier networks. We then use mathematical tools available from the world of arithmetic circuits to prove new results. First, we show that convolutional rectifier networks are universal with max pooling but not with average pooling. Second, and more importantly, we show that depth efficiency is weaker with convolutional rectifier networks than it is with convolutional arithmetic circuits. This leads us to believe that developing effective methods for training convolutional arithmetic circuits, thereby fulfilling their expressive potential, may give rise to a deep learning architecture that is provably superior to convolutional rectifier networks but has so far been overlooked by practitioners.

On the Sample Complexity of End-to-end Training vs. Semantic Abstraction Training

We compare the end-to-end training approach to a modular approach in which a system is decomposed into semantically meaningful components. We focus on the sample complexity aspect, in the regime where an extremely high accuracy is necessary, as is the case in autonomous driving applications. We demonstrate cases in which the number of training examples required by the end-to-end approach is exponentially larger than the number of examples required by the semantic abstraction approach.

Deep SimNets

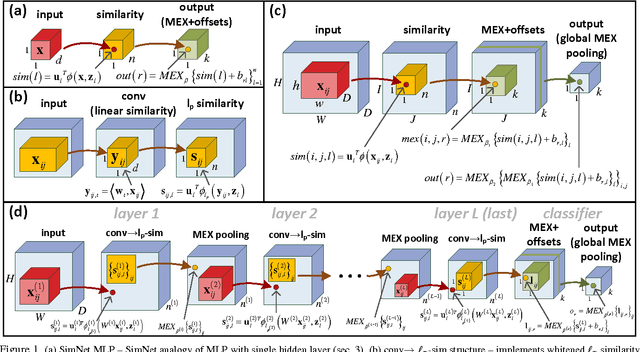
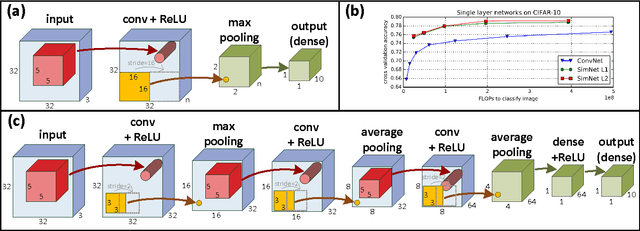
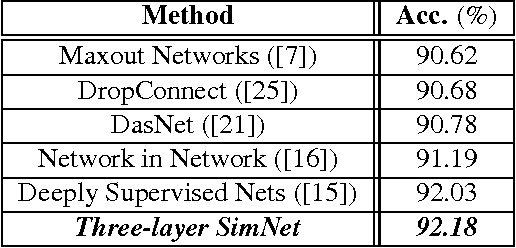
We present a deep layered architecture that generalizes convolutional neural networks (ConvNets). The architecture, called SimNets, is driven by two operators: (i) a similarity function that generalizes inner-product, and (ii) a log-mean-exp function called MEX that generalizes maximum and average. The two operators applied in succession give rise to a standard neuron but in "feature space". The feature spaces realized by SimNets depend on the choice of the similarity operator. The simplest setting, which corresponds to a convolution, realizes the feature space of the Exponential kernel, while other settings realize feature spaces of more powerful kernels (Generalized Gaussian, which includes as special cases RBF and Laplacian), or even dynamically learned feature spaces (Generalized Multiple Kernel Learning). As a result, the SimNet contains a higher abstraction level compared to a traditional ConvNet. We argue that enhanced expressiveness is important when the networks are small due to run-time constraints (such as those imposed by mobile applications). Empirical evaluation validates the superior expressiveness of SimNets, showing a significant gain in accuracy over ConvNets when computational resources at run-time are limited. We also show that in large-scale settings, where computational complexity is less of a concern, the additional capacity of SimNets can be controlled with proper regularization, yielding accuracies comparable to state of the art ConvNets.

Long-term Planning by Short-term Prediction

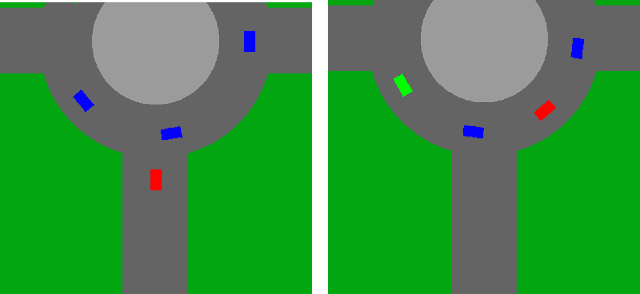
We consider planning problems, that often arise in autonomous driving applications, in which an agent should decide on immediate actions so as to optimize a long term objective. For example, when a car tries to merge in a roundabout it should decide on an immediate acceleration/braking command, while the long term effect of the command is the success/failure of the merge. Such problems are characterized by continuous state and action spaces, and by interaction with multiple agents, whose behavior can be adversarial. We argue that dual versions of the MDP framework (that depend on the value function and the $Q$ function) are problematic for autonomous driving applications due to the non Markovian of the natural state space representation, and due to the continuous state and action spaces. We propose to tackle the planning task by decomposing the problem into two phases: First, we apply supervised learning for predicting the near future based on the present. We require that the predictor will be differentiable with respect to the representation of the present. Second, we model a full trajectory of the agent using a recurrent neural network, where unexplained factors are modeled as (additive) input nodes. This allows us to solve the long-term planning problem using supervised learning techniques and direct optimization over the recurrent neural network. Our approach enables us to learn robust policies by incorporating adversarial elements to the environment.

SimNets: A Generalization of Convolutional Networks

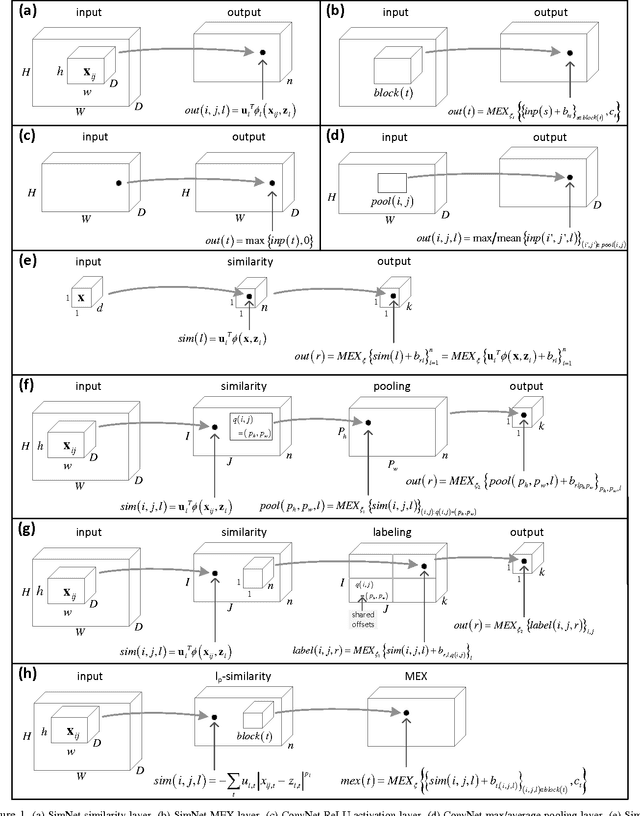
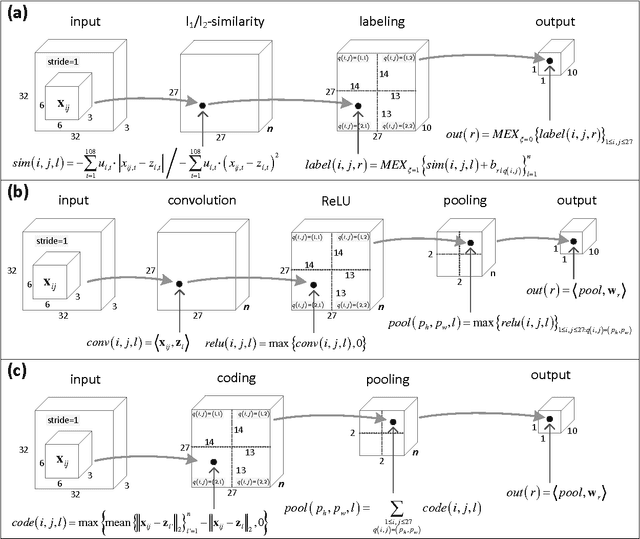
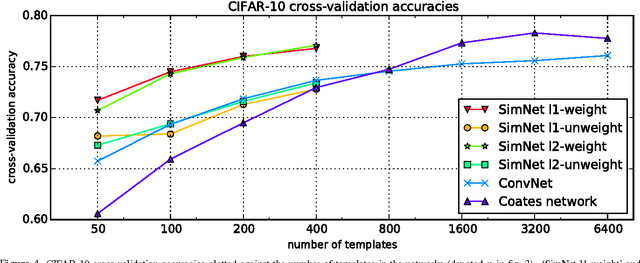
We present a deep layered architecture that generalizes classical convolutional neural networks (ConvNets). The architecture, called SimNets, is driven by two operators, one being a similarity function whose family contains the convolution operator used in ConvNets, and the other is a new soft max-min-mean operator called MEX that realizes classical operators like ReLU and max pooling, but has additional capabilities that make SimNets a powerful generalization of ConvNets. Three interesting properties emerge from the architecture: (i) the basic input to hidden layer to output machinery contains as special cases kernel machines with the Exponential and Generalized Gaussian kernels, the output units being "neurons in feature space" (ii) in its general form, the basic machinery has a higher abstraction level than kernel machines, and (iii) initializing networks using unsupervised learning is natural. Experiments demonstrate the capability of achieving state of the art accuracy with networks that are an order of magnitude smaller than comparable ConvNets.

Tightening Fractional Covering Upper Bounds on the Partition Function for High-Order Region Graphs

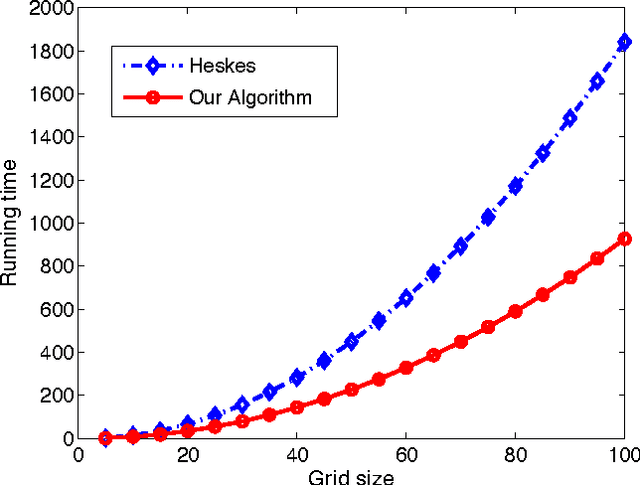
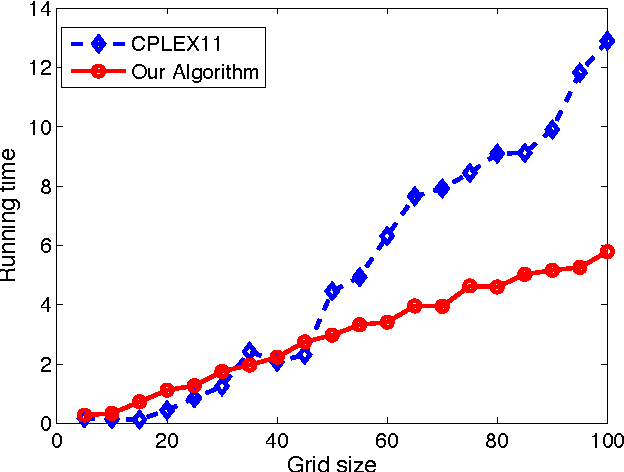
In this paper we present a new approach for tightening upper bounds on the partition function. Our upper bounds are based on fractional covering bounds on the entropy function, and result in a concave program to compute these bounds and a convex program to tighten them. To solve these programs effectively for general region graphs we utilize the entropy barrier method, thus decomposing the original programs by their dual programs and solve them with dual block optimization scheme. The entropy barrier method provides an elegant framework to generalize the message-passing scheme to high-order region graph, as well as to solve the block dual steps in closed-form. This is a key for computational relevancy for large problems with thousands of regions.