On a Formal Model of Safe and Scalable Self-driving Cars

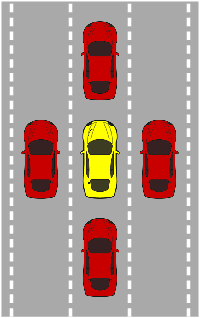
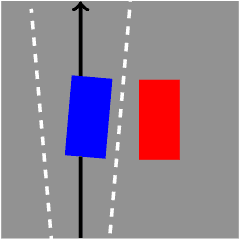
In recent years, car makers and tech companies have been racing towards self driving cars. It seems that the main parameter in this race is who will have the first car on the road. The goal of this paper is to add to the equation two additional crucial parameters. The first is standardization of safety assurance --- what are the minimal requirements that every self-driving car must satisfy, and how can we verify these requirements. The second parameter is scalability --- engineering solutions that lead to unleashed costs will not scale to millions of cars, which will push interest in this field into a niche academic corner, and drive the entire field into a "winter of autonomous driving". In the first part of the paper we propose a white-box, interpretable, mathematical model for safety assurance, which we call Responsibility-Sensitive Safety (RSS). In the second part we describe a design of a system that adheres to our safety assurance requirements and is scalable to millions of cars.

Analysis and Design of Convolutional Networks via Hierarchical Tensor Decompositions

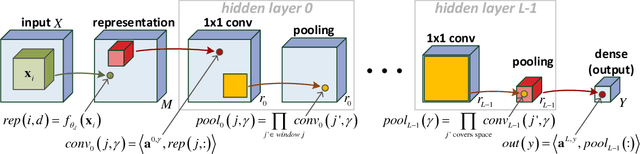
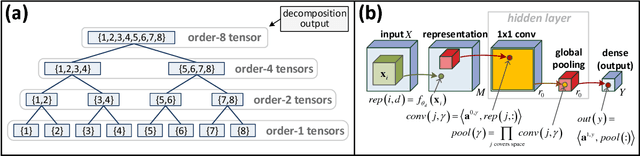
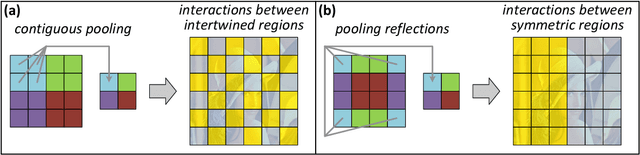
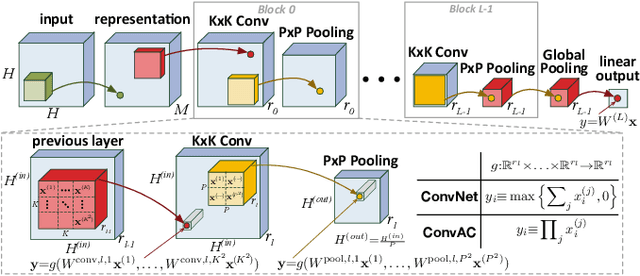
The driving force behind convolutional networks - the most successful deep learning architecture to date, is their expressive power. Despite its wide acceptance and vast empirical evidence, formal analyses supporting this belief are scarce. The primary notions for formally reasoning about expressiveness are efficiency and inductive bias. Expressive efficiency refers to the ability of a network architecture to realize functions that require an alternative architecture to be much larger. Inductive bias refers to the prioritization of some functions over others given prior knowledge regarding a task at hand. In this paper we overview a series of works written by the authors, that through an equivalence to hierarchical tensor decompositions, analyze the expressive efficiency and inductive bias of various convolutional network architectural features (depth, width, strides and more). The results presented shed light on the demonstrated effectiveness of convolutional networks, and in addition, provide new tools for network design.

On the Long-Term Memory of Deep Recurrent Networks

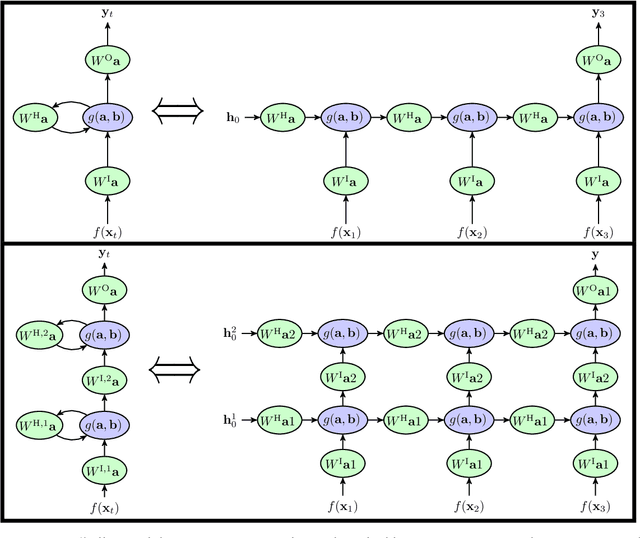
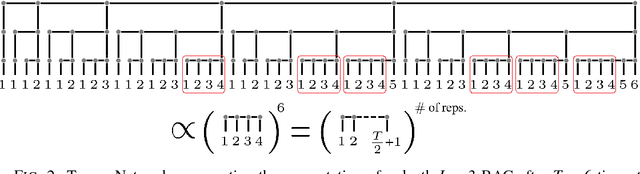
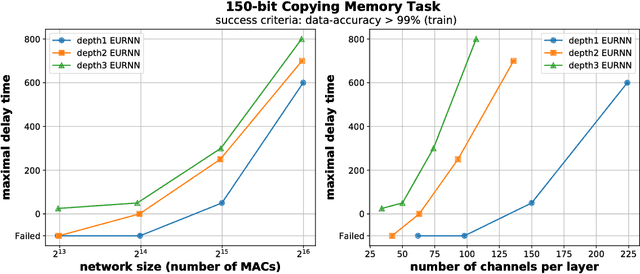
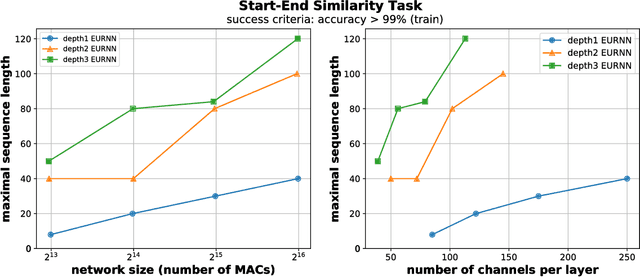
A key attribute that drives the unprecedented success of modern Recurrent Neural Networks (RNNs) on learning tasks which involve sequential data, is their ability to model intricate long-term temporal dependencies. However, a well established measure of RNNs long-term memory capacity is lacking, and thus formal understanding of the effect of depth on their ability to correlate data throughout time is limited. Specifically, existing depth efficiency results on convolutional networks do not suffice in order to account for the success of deep RNNs on data of varying lengths. In order to address this, we introduce a measure of the network's ability to support information flow across time, referred to as the Start-End separation rank, which reflects the distance of the function realized by the recurrent network from modeling no dependency between the beginning and end of the input sequence. We prove that deep recurrent networks support Start-End separation ranks which are combinatorially higher than those supported by their shallow counterparts. Thus, we establish that depth brings forth an overwhelming advantage in the ability of recurrent networks to model long-term dependencies, and provide an exemplar of quantifying this key attribute which may be readily extended to other RNN architectures of interest, e.g. variants of LSTM networks. We obtain our results by considering a class of recurrent networks referred to as Recurrent Arithmetic Circuits, which merge the hidden state with the input via the Multiplicative Integration operation, and empirically demonstrate the discussed phenomena on common RNNs. Finally, we employ the tool of quantum Tensor Networks to gain additional graphic insight regarding the complexity brought forth by depth in recurrent networks.

Bridging Many-Body Quantum Physics and Deep Learning via Tensor Networks

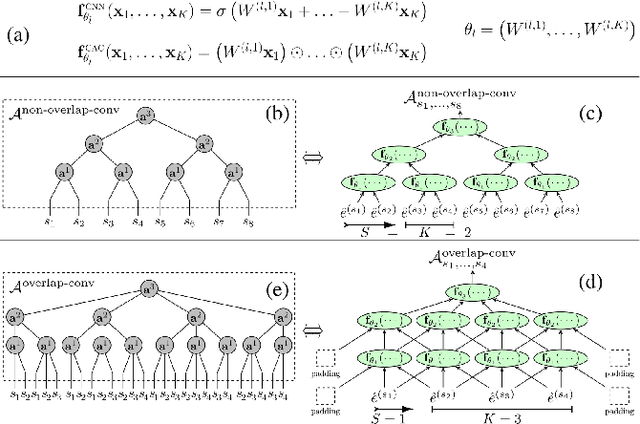
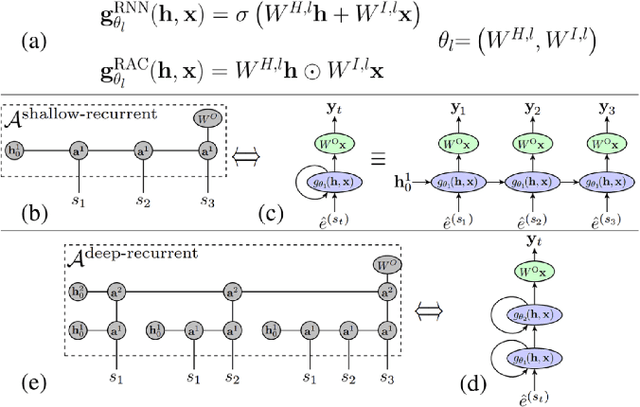
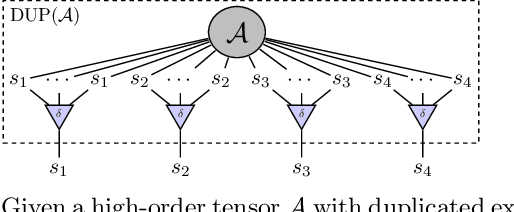
The harnessing of modern computational abilities for many-body wave-function representations is naturally placed as a prominent avenue in contemporary condensed matter physics. Specifically, highly expressive computational schemes that are able to efficiently represent the entanglement properties of many-particle systems are of interest. In the seemingly unrelated field of machine learning, deep network architectures have exhibited an unprecedented ability to tractably encompass the dependencies characterizing hard learning tasks such as image classification. However, key questions regarding deep learning architecture design still have no adequate theoretical answers. In this paper, we establish a Tensor Network (TN) based common language between the two disciplines, which allows us to offer bidirectional contributions. By showing that many-body wave-functions are structurally equivalent to mappings of ConvACs and RACs, we construct their TN equivalents, and suggest quantum entanglement measures as natural quantifiers of dependencies in such networks. Accordingly, we propose a novel entanglement based deep learning design scheme. In the other direction, we identify that an inherent re-use of information in state-of-the-art deep learning architectures is a key trait that distinguishes them from standard TNs. Therefore, we employ a TN manifestation of information re-use and construct TNs corresponding to powerful architectures such as deep recurrent and overlapping convolutional networks. This allows us to demonstrate that the entanglement scaling supported by state-of-the-art deep learning architectures matches that of MERA TN in 1D, and that they support volume law entanglement in 2D polynomially more efficiently than RBMs. We thus provide theoretical motivation to shift trending neural-network based wave-function representations closer to state-of-the-art deep learning architectures.

Tensorial Mixture Models

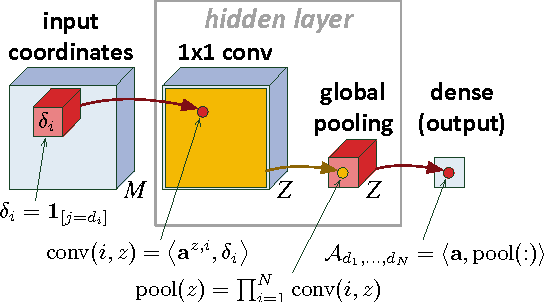
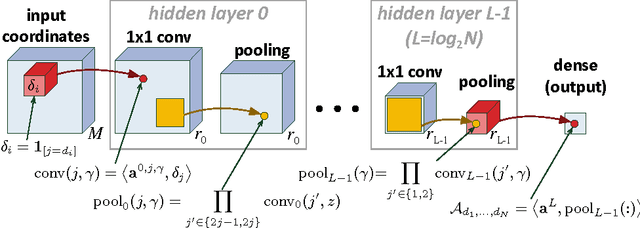
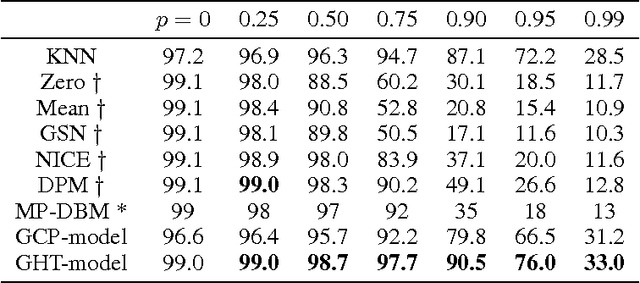
Casting neural networks in generative frameworks is a highly sought-after endeavor these days. Contemporary methods, such as Generative Adversarial Networks, capture some of the generative capabilities, but not all. In particular, they lack the ability of tractable marginalization, and thus are not suitable for many tasks. Other methods, based on arithmetic circuits and sum-product networks, do allow tractable marginalization, but their performance is challenged by the need to learn the structure of a circuit. Building on the tractability of arithmetic circuits, we leverage concepts from tensor analysis, and derive a family of generative models we call Tensorial Mixture Models (TMMs). TMMs assume a simple convolutional network structure, and in addition, lend themselves to theoretical analyses that allow comprehensive understanding of the relation between their structure and their expressive properties. We thus obtain a generative model that is tractable on one hand, and on the other hand, allows effective representation of rich distributions in an easily controlled manner. These two capabilities are brought together in the task of classification under missing data, where TMMs deliver state of the art accuracies with seamless implementation and design.

On the Expressive Power of Overlapping Architectures of Deep Learning

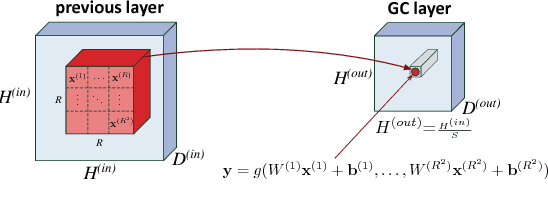
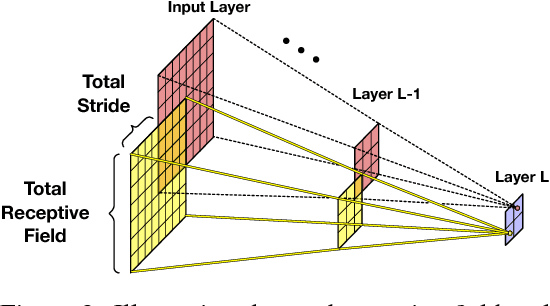
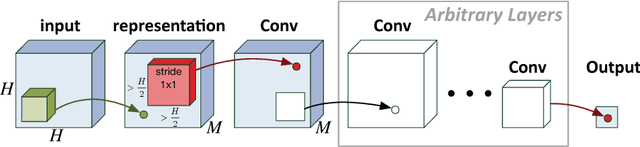
Expressive efficiency refers to the relation between two architectures A and B, whereby any function realized by B could be replicated by A, but there exists functions realized by A, which cannot be replicated by B unless its size grows significantly larger. For example, it is known that deep networks are exponentially efficient with respect to shallow networks, in the sense that a shallow network must grow exponentially large in order to approximate the functions represented by a deep network of polynomial size. In this work, we extend the study of expressive efficiency to the attribute of network connectivity and in particular to the effect of "overlaps" in the convolutional process, i.e., when the stride of the convolution is smaller than its filter size (receptive field). To theoretically analyze this aspect of network's design, we focus on a well-established surrogate for ConvNets called Convolutional Arithmetic Circuits (ConvACs), and then demonstrate empirically that our results hold for standard ConvNets as well. Specifically, our analysis shows that having overlapping local receptive fields, and more broadly denser connectivity, results in an exponential increase in the expressive capacity of neural networks. Moreover, while denser connectivity can increase the expressive capacity, we show that the most common types of modern architectures already exhibit exponential increase in expressivity, without relying on fully-connected layers.

Sum-Product-Quotient Networks

We present a novel tractable generative model that extends Sum-Product Networks (SPNs) and significantly boosts their power. We call it Sum-Product-Quotient Networks (SPQNs), whose core concept is to incorporate conditional distributions into the model by direct computation using quotient nodes, e.g. $P(A|B) = \frac{P(A,B)}{P(B)}$. We provide sufficient conditions for the tractability of SPQNs that generalize and relax the decomposable and complete tractability conditions of SPNs. These relaxed conditions give rise to an exponential boost to the expressive efficiency of our model, i.e. we prove that there are distributions which SPQNs can compute efficiently but require SPNs to be of exponential size. Thus, we narrow the gap in expressivity between tractable graphical models and other Neural Network-based generative models.

Boosting Dilated Convolutional Networks with Mixed Tensor Decompositions

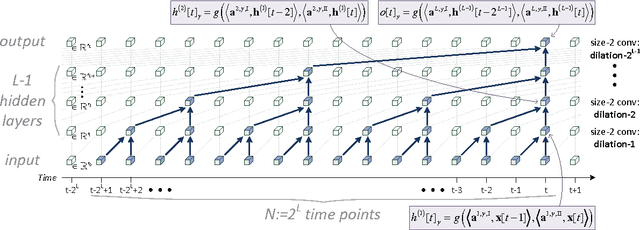
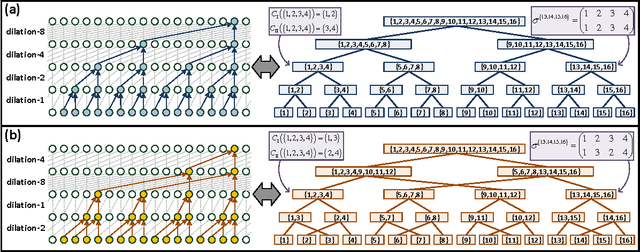
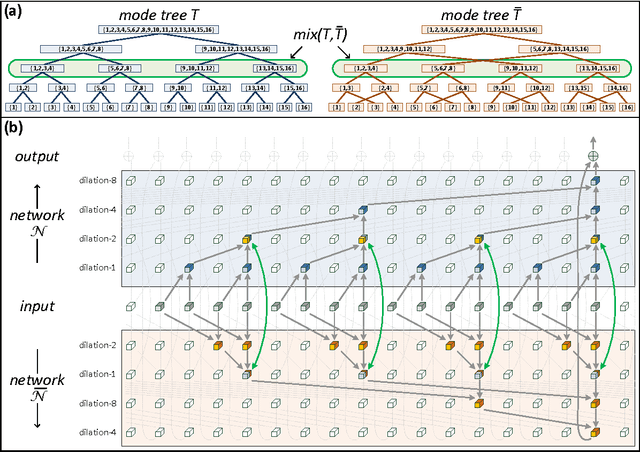
The driving force behind deep networks is their ability to compactly represent rich classes of functions. The primary notion for formally reasoning about this phenomenon is expressive efficiency, which refers to a situation where one network must grow unfeasibly large in order to realize (or approximate) functions of another. To date, expressive efficiency analyses focused on the architectural feature of depth, showing that deep networks are representationally superior to shallow ones. In this paper we study the expressive efficiency brought forth by connectivity, motivated by the observation that modern networks interconnect their layers in elaborate ways. We focus on dilated convolutional networks, a family of deep models delivering state of the art performance in sequence processing tasks. By introducing and analyzing the concept of mixed tensor decompositions, we prove that interconnecting dilated convolutional networks can lead to expressive efficiency. In particular, we show that even a single connection between intermediate layers can already lead to an almost quadratic gap, which in large-scale settings typically makes the difference between a model that is practical and one that is not. Empirical evaluation demonstrates how the expressive efficiency of connectivity, similarly to that of depth, translates into gains in accuracy. This leads us to believe that expressive efficiency may serve a key role in the development of new tools for deep network design.

Inductive Bias of Deep Convolutional Networks through Pooling Geometry

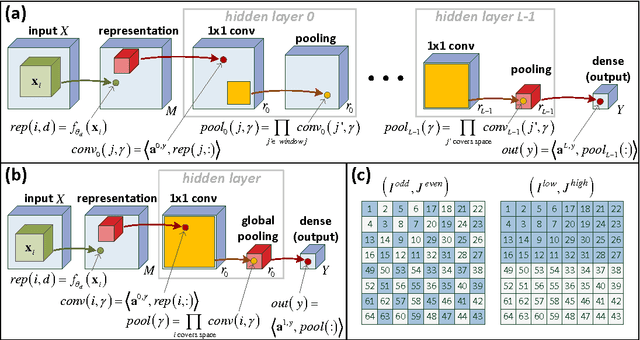
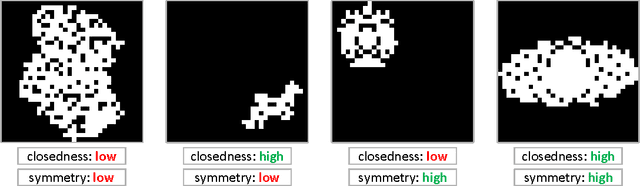
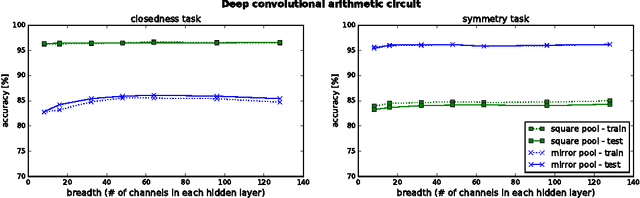
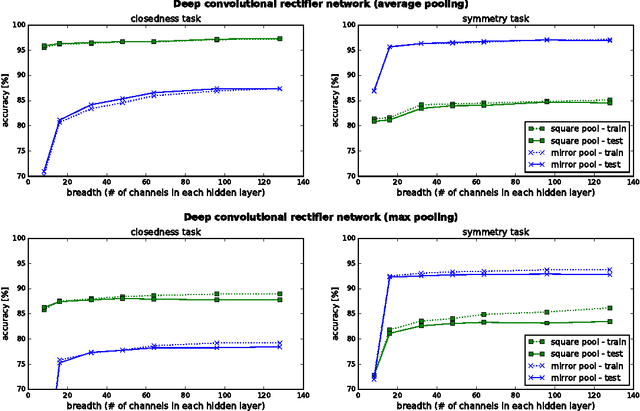
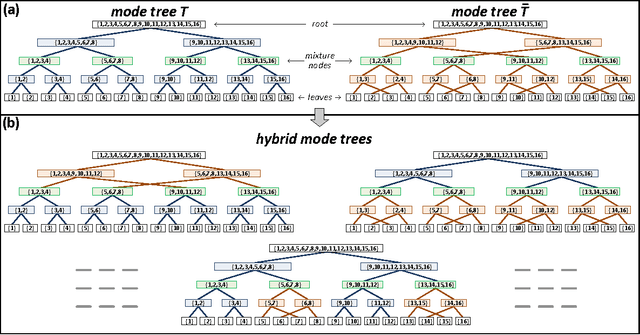
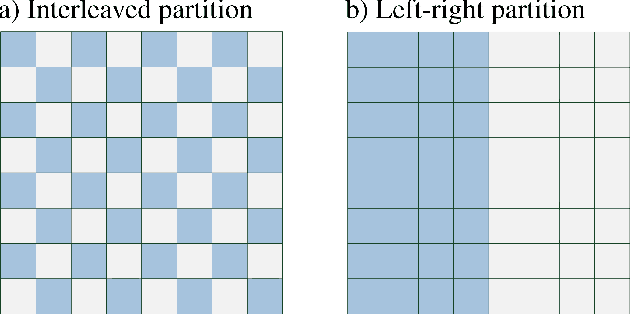
Our formal understanding of the inductive bias that drives the success of convolutional networks on computer vision tasks is limited. In particular, it is unclear what makes hypotheses spaces born from convolution and pooling operations so suitable for natural images. In this paper we study the ability of convolutional networks to model correlations among regions of their input. We theoretically analyze convolutional arithmetic circuits, and empirically validate our findings on other types of convolutional networks as well. Correlations are formalized through the notion of separation rank, which for a given partition of the input, measures how far a function is from being separable. We show that a polynomially sized deep network supports exponentially high separation ranks for certain input partitions, while being limited to polynomial separation ranks for others. The network's pooling geometry effectively determines which input partitions are favored, thus serves as a means for controlling the inductive bias. Contiguous pooling windows as commonly employed in practice favor interleaved partitions over coarse ones, orienting the inductive bias towards the statistics of natural images. Other pooling schemes lead to different preferences, and this allows tailoring the network to data that departs from the usual domain of natural imagery. In addition to analyzing deep networks, we show that shallow ones support only linear separation ranks, and by this gain insight into the benefit of functions brought forth by depth - they are able to efficiently model strong correlation under favored partitions of the input.

Deep Learning and Quantum Entanglement: Fundamental Connections with Implications to Network Design

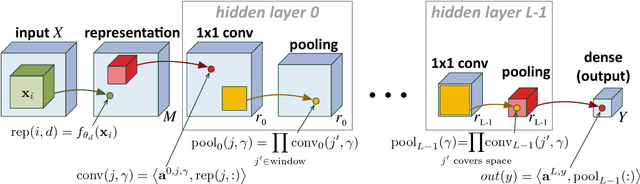
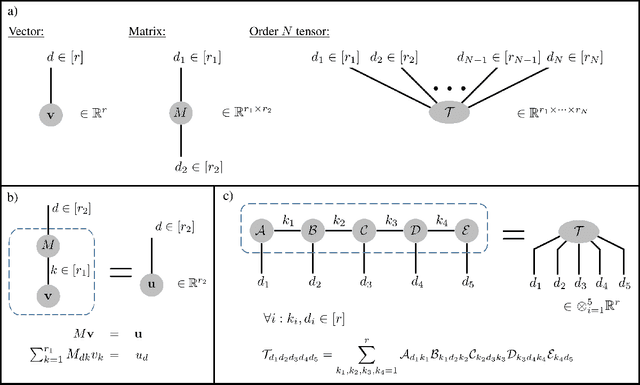
Deep convolutional networks have witnessed unprecedented success in various machine learning applications. Formal understanding on what makes these networks so successful is gradually unfolding, but for the most part there are still significant mysteries to unravel. The inductive bias, which reflects prior knowledge embedded in the network architecture, is one of them. In this work, we establish a fundamental connection between the fields of quantum physics and deep learning. We use this connection for asserting novel theoretical observations regarding the role that the number of channels in each layer of the convolutional network fulfills in the overall inductive bias. Specifically, we show an equivalence between the function realized by a deep convolutional arithmetic circuit (ConvAC) and a quantum many-body wave function, which relies on their common underlying tensorial structure. This facilitates the use of quantum entanglement measures as well-defined quantifiers of a deep network's expressive ability to model intricate correlation structures of its inputs. Most importantly, the construction of a deep ConvAC in terms of a Tensor Network is made available. This description enables us to carry a graph-theoretic analysis of a convolutional network, with which we demonstrate a direct control over the inductive bias of the deep network via its channel numbers, that are related to the min-cut in the underlying graph. This result is relevant to any practitioner designing a network for a specific task. We theoretically analyze ConvACs, and empirically validate our findings on more common ConvNets which involve ReLU activations and max pooling. Beyond the results described above, the description of a deep convolutional network in well-defined graph-theoretic tools and the formal connection to quantum entanglement, are two interdisciplinary bridges that are brought forth by this work.