BrainATCL: Adaptive Temporal Brain Connectivity Learning for Functional Link Prediction and Age Estimation

Functional Magnetic Resonance Imaging (fMRI) is an imaging technique widely used to study human brain activity. fMRI signals in areas across the brain transiently synchronise and desynchronise their activity in a highly structured manner, even when an individual is at rest. These functional connectivity dynamics may be related to behaviour and neuropsychiatric disease. To model these dynamics, temporal brain connectivity representations are essential, as they reflect evolving interactions between brain regions and provide insight into transient neural states and network reconfigurations. However, conventional graph neural networks (GNNs) often struggle to capture long-range temporal dependencies in dynamic fMRI data. To address this challenge, we propose BrainATCL, an unsupervised, nonparametric framework for adaptive temporal brain connectivity learning, enabling functional link prediction and age estimation. Our method dynamically adjusts the lookback window for each snapshot based on the rate of newly added edges. Graph sequences are subsequently encoded using a GINE-Mamba2 backbone to learn spatial-temporal representations of dynamic functional connectivity in resting-state fMRI data of 1,000 participants from the Human Connectome Project. To further improve spatial modeling, we incorporate brain structure and function-informed edge attributes, i.e., the left/right hemispheric identity and subnetwork membership of brain regions, enabling the model to capture biologically meaningful topological patterns. We evaluate our BrainATCL on two tasks: functional link prediction and age estimation. The experimental results demonstrate superior performance and strong generalization, including in cross-session prediction scenarios.

Boundary informed inverse PDE problems on discrete Riemann surfaces

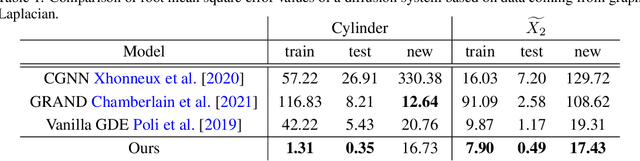
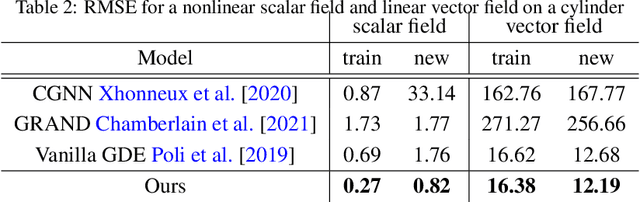
We employ neural networks to tackle inverse partial differential equations on discretized Riemann surfaces with boundary. To this end, we introduce the concept of a graph with boundary which models these surfaces in a natural way. Our method uses a message passing technique to keep track of an unknown differential operator while using neural ODE solvers through the method of lines to capture the evolution in time. As training data, we use noisy and incomplete observations of sheaves on graphs at various timestamps. The novelty of this approach is in working with manifolds with nontrivial topology and utilizing the data on the graph boundary through a teacher forcing technique. Despite the increasing interest in learning dynamical systems from finite observations, many current methods are limited in two general ways: first, they work with topologically trivial spaces, and second, they fail to handle the boundary data on the ground space in a systematic way. The present work is an attempt at addressing these limitations. We run experiments with synthetic data of linear and nonlinear diffusion systems on orientable surfaces with positive genus and boundary, and moreover, provide evidences for improvements upon the existing paradigms.

Maximum Entropy Weighted Independent Set Pooling for Graph Neural Networks

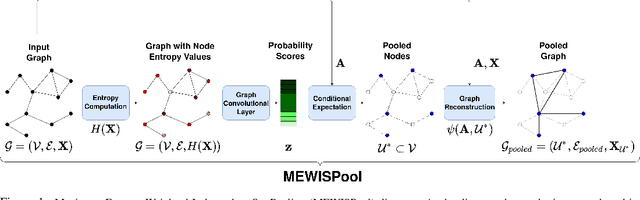
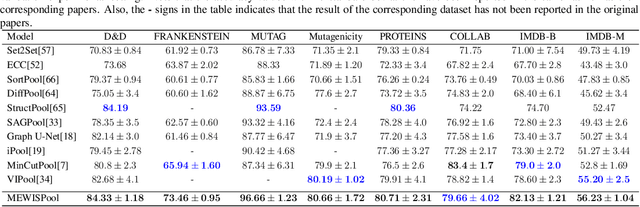
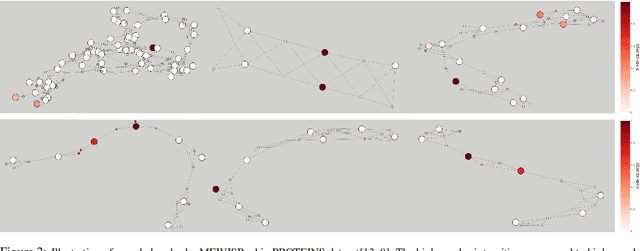
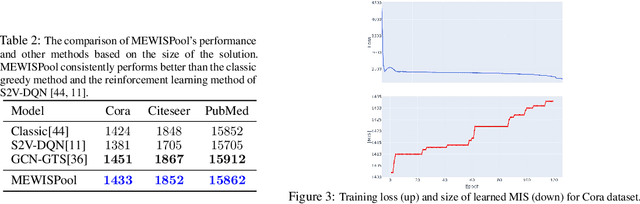
In this paper, we propose a novel pooling layer for graph neural networks based on maximizing the mutual information between the pooled graph and the input graph. Since the maximum mutual information is difficult to compute, we employ the Shannon capacity of a graph as an inductive bias to our pooling method. More precisely, we show that the input graph to the pooling layer can be viewed as a representation of a noisy communication channel. For such a channel, sending the symbols belonging to an independent set of the graph yields a reliable and error-free transmission of information. We show that reaching the maximum mutual information is equivalent to finding a maximum weight independent set of the graph where the weights convey entropy contents. Through this communication theoretic standpoint, we provide a distinct perspective for posing the problem of graph pooling as maximizing the information transmission rate across a noisy communication channel, implemented by a graph neural network. We evaluate our method, referred to as Maximum Entropy Weighted Independent Set Pooling (MEWISPool), on graph classification tasks and the combinatorial optimization problem of the maximum independent set. Empirical results demonstrate that our method achieves the state-of-the-art and competitive results on graph classification tasks and the maximum independent set problem in several benchmark datasets.