A Review on Sound Source Localization in Robotics: Focusing on Deep Learning Methods

Sound source localization (SSL) adds a spatial dimension to auditory perception, allowing a system to pinpoint the origin of speech, machinery noise, warning tones, or other acoustic events, capabilities that facilitate robot navigation, human-machine dialogue, and condition monitoring. While existing surveys provide valuable historical context, they typically address general audio applications and do not fully account for robotic constraints or the latest advancements in deep learning. This review addresses these gaps by offering a robotics-focused synthesis, emphasizing recent progress in deep learning methodologies. We start by reviewing classical methods such as Time Difference of Arrival (TDOA), beamforming, Steered-Response Power (SRP), and subspace analysis. Subsequently, we delve into modern machine learning (ML) and deep learning (DL) approaches, discussing traditional ML and neural networks (NNs), convolutional neural networks (CNNs), convolutional recurrent neural networks (CRNNs), and emerging attention-based architectures. The data and training strategy that are the two cornerstones of DL-based SSL are explored. Studies are further categorized by robot types and application domains to facilitate researchers in identifying relevant work for their specific contexts. Finally, we highlight the current challenges in SSL works in general, regarding environmental robustness, sound source multiplicity, and specific implementation constraints in robotics, as well as data and learning strategies in DL-based SSL. Also, we sketch promising directions to offer an actionable roadmap toward robust, adaptable, efficient, and explainable DL-based SSL for next-generation robots.

PDR-CapsNet: an Energy-Efficient Parallel Approach to Dynamic Routing in Capsule Networks

Convolutional Neural Networks (CNNs) have produced state-of-the-art results for image classification tasks. However, they are limited in their ability to handle rotational and viewpoint variations due to information loss in max-pooling layers. Capsule Networks (CapsNets) employ a computationally-expensive iterative process referred to as dynamic routing to address these issues. CapsNets, however, often fall short on complex datasets and require more computational resources than CNNs. To overcome these challenges, we introduce the Parallel Dynamic Routing CapsNet (PDR-CapsNet), a deeper and more energy-efficient alternative to CapsNet that offers superior performance, less energy consumption, and lower overfitting rates. By leveraging a parallelization strategy, PDR-CapsNet mitigates the computational complexity of CapsNet and increases throughput, efficiently using hardware resources. As a result, we achieve 83.55\% accuracy while requiring 87.26\% fewer parameters, 32.27\% and 47.40\% fewer MACs, and Flops, achieving 3x faster inference and 7.29J less energy consumption on a 2080Ti GPU with 11GB VRAM compared to CapsNet and for the CIFAR-10 dataset.

Quantum Annealing Approaches to the Phase-Unwrapping Problem in Synthetic-Aperture Radar Imaging

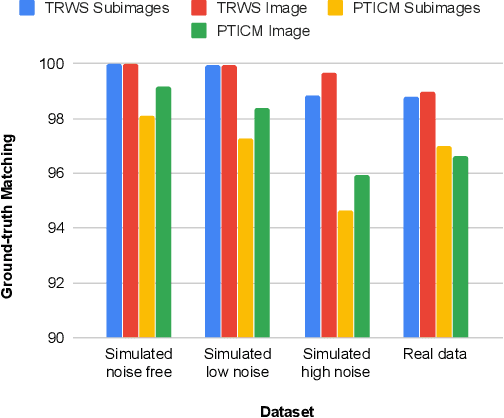
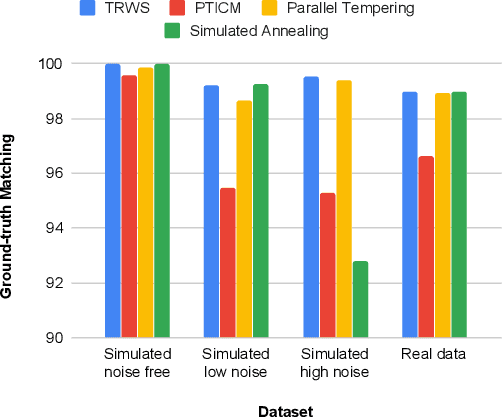
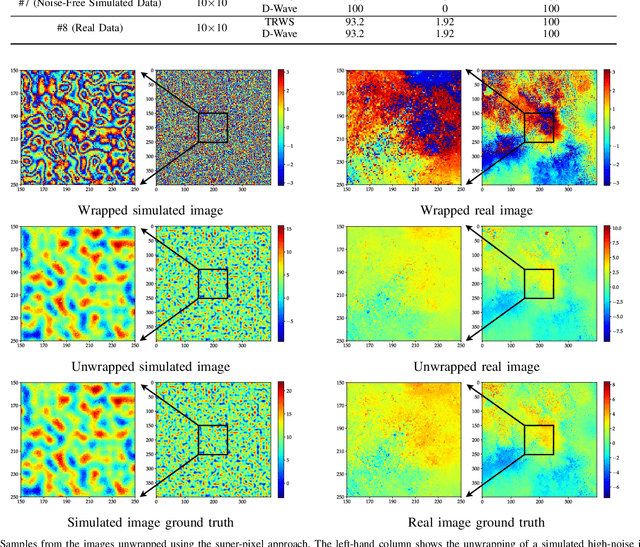
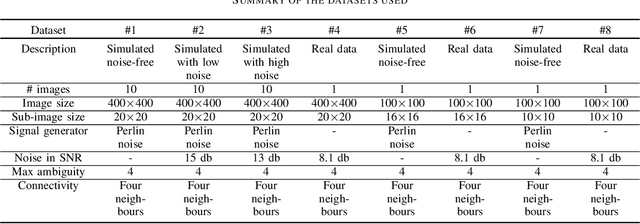
The focus of this work is to explore the use of quantum annealing solvers for the problem of phase unwrapping of synthetic aperture radar (SAR) images. Although solutions to this problem exist based on network programming, these techniques do not scale well to larger-sized images. Our approach involves formulating the problem as a quadratic unconstrained binary optimization (QUBO) problem, which can be solved using a quantum annealer. Given that present embodiments of quantum annealers remain limited in the number of qubits they possess, we decompose the problem into a set of subproblems that can be solved individually. These individual solutions are close to optimal up to an integer constant, with one constant per sub-image. In a second phase, these integer constants are determined as a solution to yet another QUBO problem. We test our approach with a variety of software-based QUBO solvers and on a variety of images, both synthetic and real. Additionally, we experiment using D-Wave Systems's quantum annealer, the D-Wave 2000Q. The software-based solvers obtain high-quality solutions comparable to state-of-the-art phase-unwrapping solvers. We are currently working on optimally mapping the problem onto the restricted topology of the quantum annealer to improve the quality of the solution.