Ambuj Tewari
University of Texas
Representation Learning Beyond Linear Prediction Functions
May 31, 2021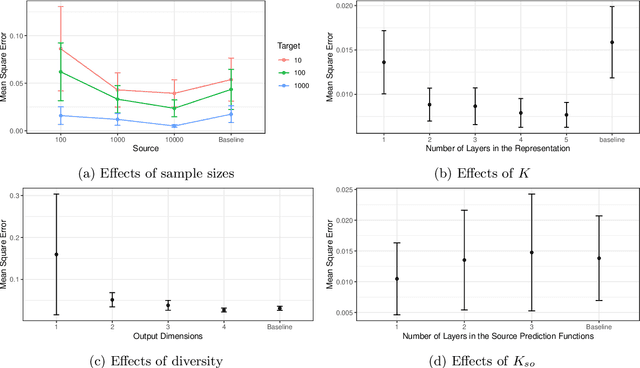
Abstract:Recent papers on the theory of representation learning has shown the importance of a quantity called diversity when generalizing from a set of source tasks to a target task. Most of these papers assume that the function mapping shared representations to predictions is linear, for both source and target tasks. In practice, researchers in deep learning use different numbers of extra layers following the pretrained model based on the difficulty of the new task. This motivates us to ask whether diversity can be achieved when source tasks and the target task use different prediction function spaces beyond linear functions. We show that diversity holds even if the target task uses a neural network with multiple layers, as long as source tasks use linear functions. If source tasks use nonlinear prediction functions, we provide a negative result by showing that depth-1 neural networks with ReLu activation function need exponentially many source tasks to achieve diversity. For a general function class, we find that eluder dimension gives a lower bound on the number of tasks required for diversity. Our theoretical results imply that simpler tasks generalize better. Though our theoretical results are shown for the global minimizer of empirical risks, their qualitative predictions still hold true for gradient-based optimization algorithms as verified by our simulations on deep neural networks.
Causal Markov Decision Processes: Learning Good Interventions Efficiently
Feb 15, 2021
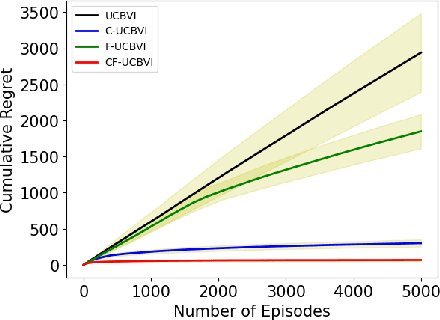
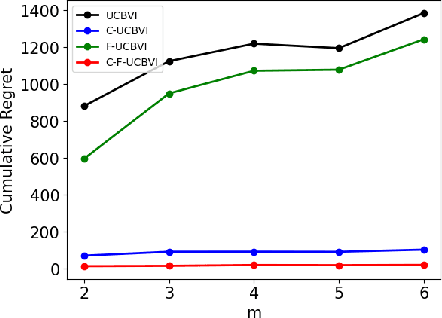
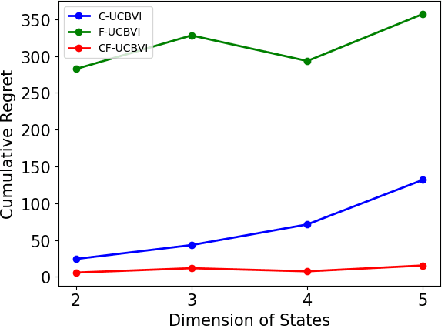
Abstract:We introduce causal Markov Decision Processes (C-MDPs), a new formalism for sequential decision making which combines the standard MDP formulation with causal structures over state transition and reward functions. Many contemporary and emerging application areas such as digital healthcare and digital marketing can benefit from modeling with C-MDPs due to the causal mechanisms underlying the relationship between interventions and states/rewards. We propose the causal upper confidence bound value iteration (C-UCBVI) algorithm that exploits the causal structure in C-MDPs and improves the performance of standard reinforcement learning algorithms that do not take causal knowledge into account. We prove that C-UCBVI satisfies an $\tilde{O}(HS\sqrt{ZT})$ regret bound, where $T$ is the the total time steps, $H$ is the episodic horizon, and $S$ is the cardinality of the state space. Notably, our regret bound does not scale with the size of actions/interventions ($A$), but only scales with a causal graph dependent quantity $Z$ which can be exponentially smaller than $A$. By extending C-UCBVI to the factored MDP setting, we propose the causal factored UCBVI (CF-UCBVI) algorithm, which further reduces the regret exponentially in terms of $S$. Furthermore, we show that RL algorithms for linear MDP problems can also be incorporated in C-MDPs. We empirically show the benefit of our causal approaches in various settings to validate our algorithms and theoretical results.
Decision Making Problems with Funnel Structure: A Multi-Task Learning Approach with Application to Email Marketing Campaigns
Oct 15, 2020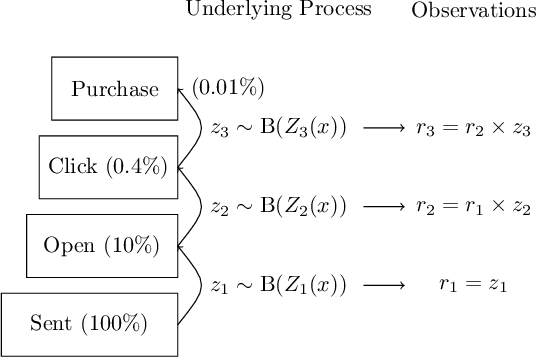
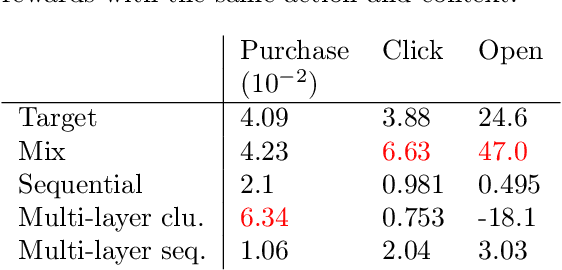
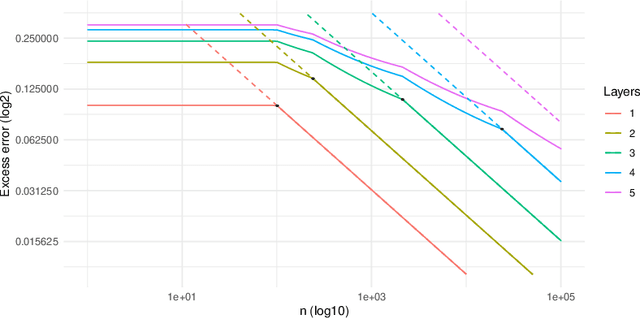
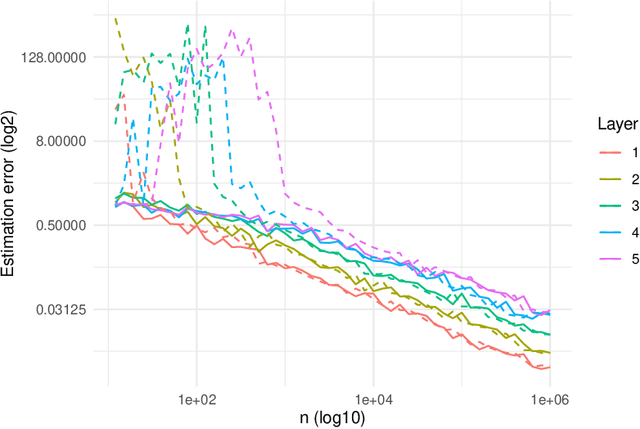
Abstract:This paper studies the decision making problem with Funnel Structure. Funnel structure, a well-known concept in the marketing field, occurs in those systems where the decision maker interacts with the environment in a layered manner receiving far fewer observations from deep layers than shallow ones. For example, in the email marketing campaign application, the layers correspond to Open, Click and Purchase events. Conversions from Click to Purchase happen very infrequently because a purchase cannot be made unless the link in an email is clicked on. We formulate this challenging decision making problem as a contextual bandit with funnel structure and develop a multi-task learning algorithm that mitigates the lack of sufficient observations from deeper layers. We analyze both the prediction error and the regret of our algorithms. We verify our theory on prediction errors through a simple simulation. Experiments on both a simulated environment and an environment based on real-world data from a major email marketing company show that our algorithms offer significant improvement over previous methods.
Federated Learning via Synthetic Data
Aug 11, 2020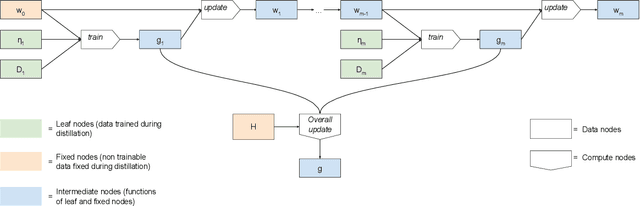
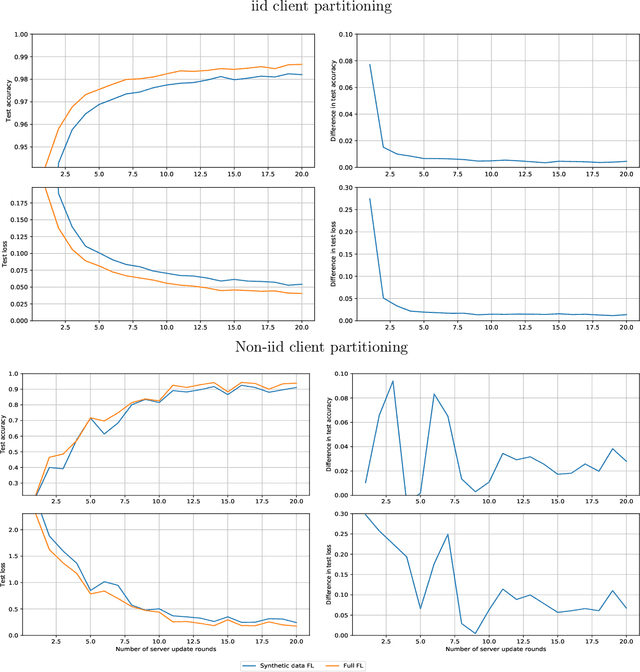
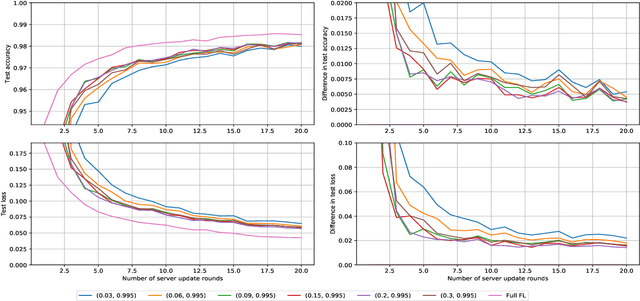
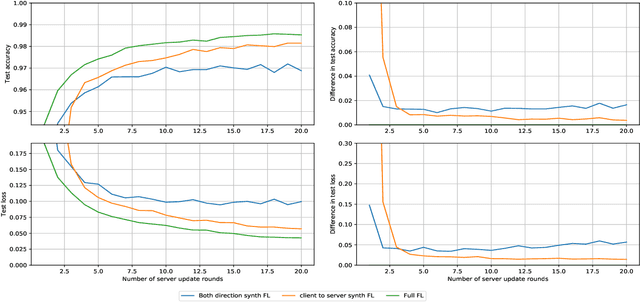
Abstract:Federated learning allows for the training of a model using data on multiple clients without the clients transmitting that raw data. However the standard method is to transmit model parameters (or updates), which for modern neural networks can be on the scale of millions of parameters, inflicting significant computational costs on the clients. We propose a method for federated learning where instead of transmitting a gradient update back to the server, we instead transmit a small amount of synthetic `data'. We describe the procedure and show some experimental results suggesting this procedure has potential, providing more than an order of magnitude reduction in communication costs with minimal model degradation.
TorsionNet: A Reinforcement Learning Approach to Sequential Conformer Search
Jun 12, 2020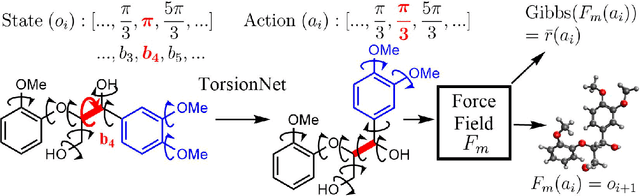
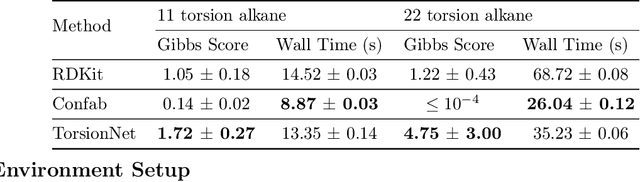
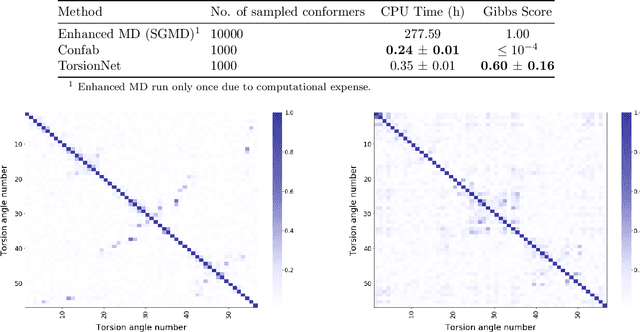
Abstract:Molecular geometry prediction of flexible molecules, or conformer search, is a long-standing challenge in computational chemistry. This task is of great importance for predicting structure-activity relationships for a wide variety of substances ranging from biomolecules to ubiquitous materials. Substantial computational resources are invested in Monte Carlo and Molecular Dynamics methods to generate diverse and representative conformer sets for medium to large molecules, which are yet intractable to chemoinformatic conformer search methods. We present TorsionNet, an efficient sequential conformer search technique based on reinforcement learning under the rigid rotor approximation. The model is trained via curriculum learning, whose theoretical benefit is explored in detail, to maximize a novel metric grounded in thermodynamics called the Gibbs Score. Our experimental results show that TorsionNet outperforms the highest scoring chemoinformatics method by 4x on large branched alkanes, and by several orders of magnitude on the previously unexplored biopolymer lignin, with applications in renewable energy.
Low-Rank Generalized Linear Bandit Problems
Jun 04, 2020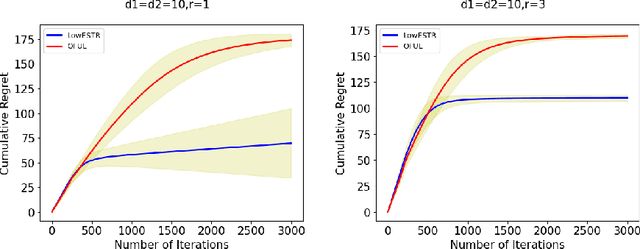
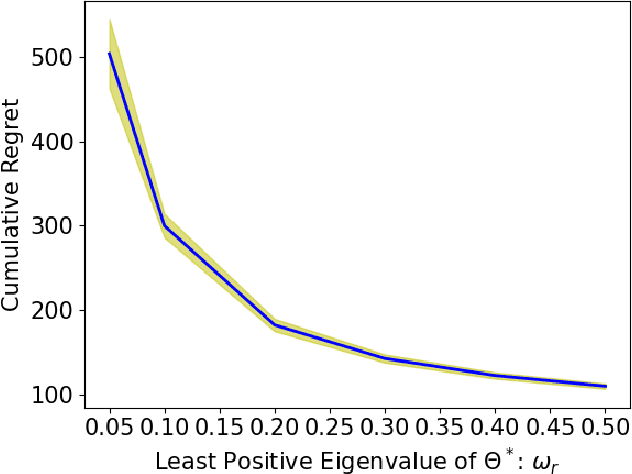
Abstract:In a low-rank linear bandit problem, the reward of an action (represented by a matrix of size $d_1 \times d_2$) is the inner product between the action and an unknown low-rank matrix $\Theta^*$. We propose an algorithm based on a novel combination of online-to-confidence-set conversion~\citep{abbasi2012online} and the exponentially weighted average forecaster constructed by a covering of low-rank matrices. In $T$ rounds, our algorithm achieves $\widetilde{O}((d_1+d_2)^{3/2}\sqrt{rT})$ regret that improves upon the standard linear bandit regret bound of $\widetilde{O}(d_1d_2\sqrt{T})$ when the rank of $\Theta^*$: $r \ll \min\{d_1,d_2\}$. We also extend our algorithmic approach to the generalized linear setting to get an algorithm which enjoys a similar bound under regularity conditions on the link function. To get around the computational intractability of covering based approaches, we propose an efficient algorithm by extending the "Explore-Subspace-Then-Refine" algorithm of~\citet{jun2019bilinear}. Our efficient algorithm achieves $\widetilde{O}((d_1+d_2)^{3/2}\sqrt{rT})$ regret under a mild condition on the action set $\mathcal{X}$ and the $r$-th singular value of $\Theta^*$. Our upper bounds match the conjectured lower bound of \cite{jun2019bilinear} for a subclass of low-rank linear bandit problems. Further, we show that existing lower bounds for the sparse linear bandit problem strongly suggest that our regret bounds are unimprovable. To complement our theoretical contributions, we also conduct experiments to demonstrate that our algorithm can greatly outperform the performance of the standard linear bandit approach when $\Theta^*$ is low-rank.
On the Equivalence between Online and Private Learnability beyond Binary Classification
Jun 02, 2020Abstract:Alon et al. [2019] and Bun et al. [2020] recently showed that online learnability and private PAC learnability are equivalent in binary classification. We investigate whether this equivalence extends to multi-class classification and regression. First, we show that private learnability implies online learnability in both settings. Our extension involves studying a novel variant of the Littlestone dimension that depends on a tolerance parameter and on an appropriate generalization of the concept of threshold functions beyond binary classification. Second, we show that while online learnability continues to imply private learnability in multi-class classification, current proof techniques encounter significant hurdles in the regression setting. While the equivalence for regression remains open, we provide non-trivial sufficient conditions for an online learnable class to also be privately learnable.
On Learnability under General Stochastic Processes
May 15, 2020Abstract:Statistical learning theory under independent and identically distributed (iid) sampling and online learning theory for worst case individual sequences are two of the best developed branches of learning theory. Statistical learning under general non-iid stochastic processes is less mature. We provide two natural notions of learnability of a function class under a general stochastic process. We are able to sandwich the first one between iid and online learnability. We show that the second one is in fact equivalent to online learnability. Our results are sharpest in the binary classification setting but we also show that similar results continue to hold in the regression setting.
Near-optimal Reinforcement Learning in Factored MDPs: Oracle-Efficient Algorithms for the Non-episodic Setting
Feb 06, 2020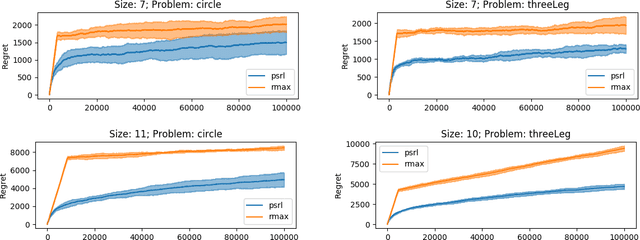
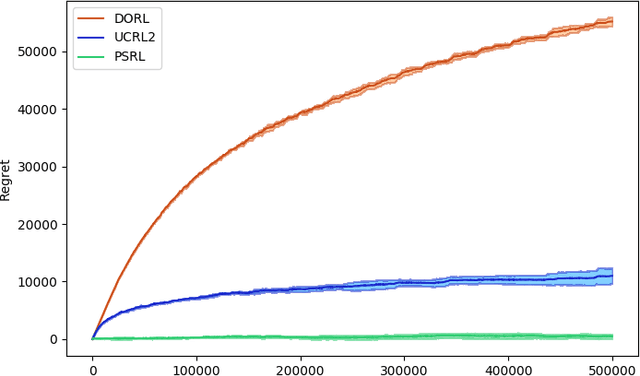
Abstract:We study reinforcement learning in factored Markov decision processes (FMDPs) in the non-episodic setting. We focus on regret analyses providing both upper and lower bounds. We propose two near-optimal and oracle-efficient algorithms for FMDPs. Assuming oracle access to an FMDP planner, they enjoy a Bayesian and a frequentist regret bound respectively, both of which reduce to the near-optimal bound $\widetilde{O}(DS\sqrt{AT})$ for standard non-factored MDPs. Our lower bound depends on the span of the bias vector rather than the diameter $D$ and we show via a simple Cartesian product construction that FMDPs with a bounded span can have an arbitrarily large diameter, which suggests that bounds with a dependence on diameter can be extremely loose. We, therefore, propose another algorithm that only depends on span but relies on a computationally stronger oracle. Our algorithms outperform the previous near-optimal algorithms on computer network administrator simulations.
Near-optimal Oracle-efficient Algorithms for Stationary and Non-Stationary Stochastic Linear Bandits
Jan 15, 2020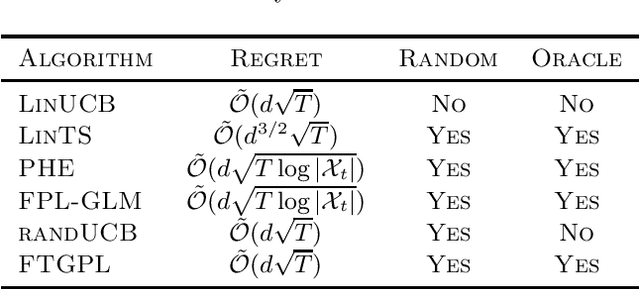
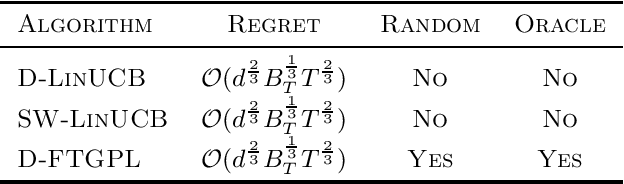
Abstract:We investigate the design of two algorithms that enjoy not only computational efficiency induced by Hannan's perturbation approach, but also minimax-optimal regret bounds in linear bandit problems where the learner has access to an offline optimization oracle. We present an algorithm called Follow-The-Gaussian-Perturbed Leader (FTGPL) for stationary linear bandit where each action is associated with a $d$-dimensional feature vector, and prove that FTGPL (1) achieves the minimax-optimal $\tilde{\mathcal{O}}(d\sqrt{T})$ regret, (2) matches the empirical performance of Linear Thompson Sampling, and (3) can be efficiently implemented even in the case of infinite actions, thus achieving the best of three worlds. Furthermore, it firmly solves an open problem raised in \citet{abeille2017linear}, which perturbation achieves minimax-optimality in Linear Thompson Sampling. The weighted variant with exponential discounting, Discounted Follow-The-Gaussian-Perturbed Leader (D-FTGPL) is proposed to gracefully adjust to non-stationary environment where unknown parameter is time-varying within total variation $B_T$. It asymptotically achieves optimal dynamic regret $\tilde{\mathcal{O}}( d ^{2/3}B_T^{1/3} T^{2/3})$ and is oracle-efficient due to access to an offline optimization oracle induced by Gaussian perturbation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge