Fair and Accurate Regression: Strong Formulations and Algorithms

This paper introduces mixed-integer optimization methods to solve regression problems that incorporate fairness metrics. We propose an exact formulation for training fair regression models. To tackle this computationally hard problem, we study the polynomially-solvable single-factor and single-observation subproblems as building blocks and derive their closed convex hull descriptions. Strong formulations obtained for the general fair regression problem in this manner are utilized to solve the problem with a branch-and-bound algorithm exactly or as a relaxation to produce fair and accurate models rapidly. Moreover, to handle large-scale instances, we develop a coordinate descent algorithm motivated by the convex-hull representation of the single-factor fair regression problem to improve a given solution efficiently. Numerical experiments conducted on fair least squares and fair logistic regression problems show competitive statistical performance with state-of-the-art methods while significantly reducing training times.

State-driven Implicit Modeling for Sparsity and Robustness in Neural Networks

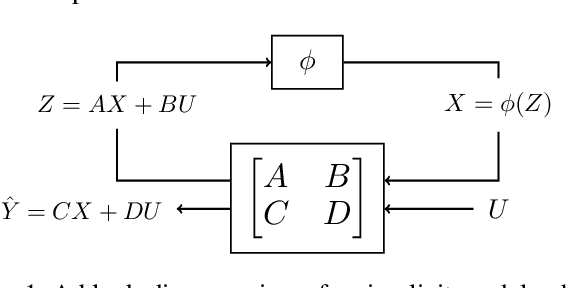
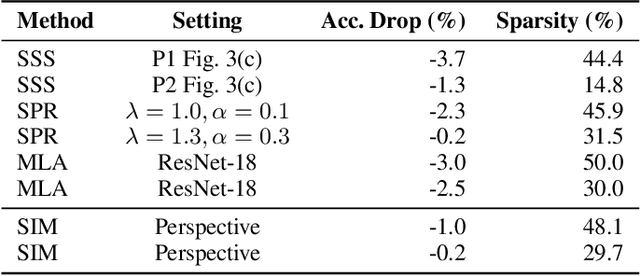
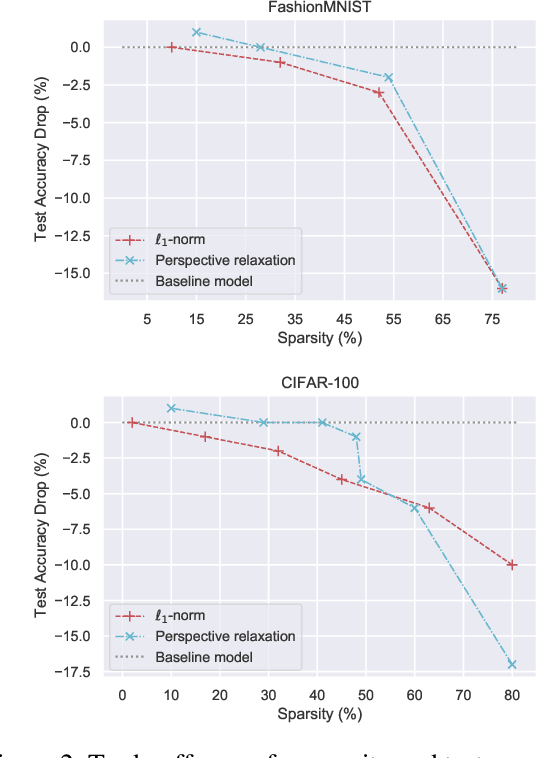
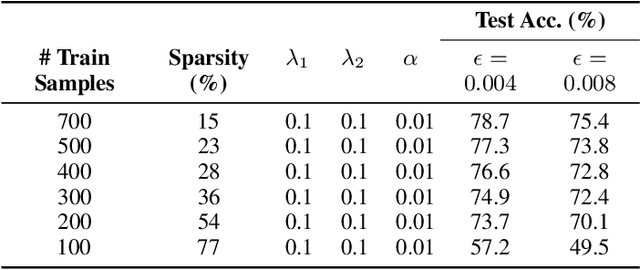
Implicit models are a general class of learning models that forgo the hierarchical layer structure typical in neural networks and instead define the internal states based on an ``equilibrium'' equation, offering competitive performance and reduced memory consumption. However, training such models usually relies on expensive implicit differentiation for backward propagation. In this work, we present a new approach to training implicit models, called State-driven Implicit Modeling (SIM), where we constrain the internal states and outputs to match that of a baseline model, circumventing costly backward computations. The training problem becomes convex by construction and can be solved in a parallel fashion, thanks to its decomposable structure. We demonstrate how the SIM approach can be applied to significantly improve sparsity (parameter reduction) and robustness of baseline models trained on FashionMNIST and CIFAR-100 datasets.

On the convex hull of convex quadratic optimization problems with indicators

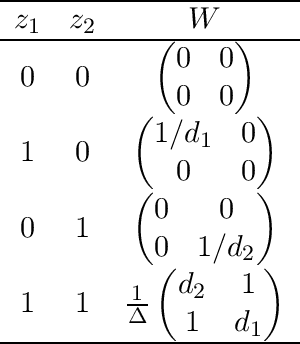
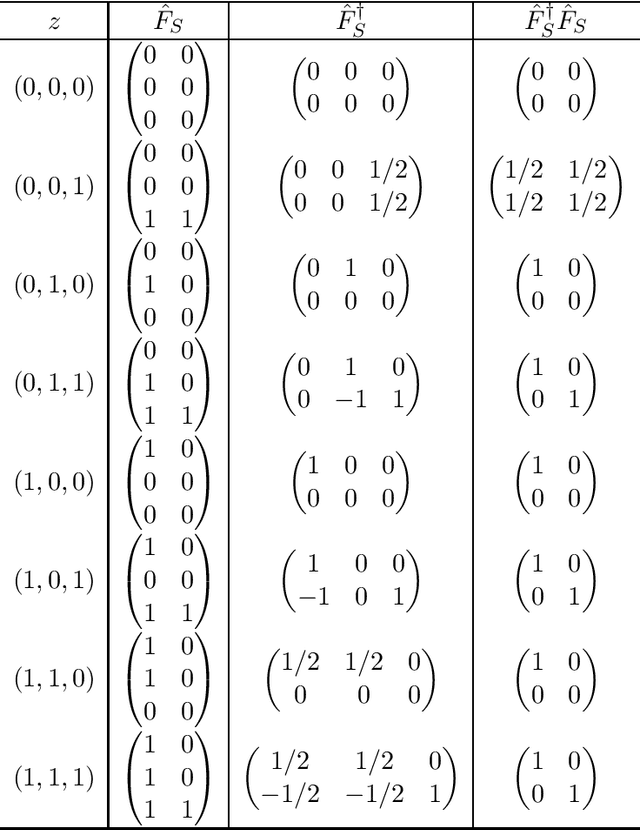
We consider the convex quadratic optimization problem with indicator variables and arbitrary constraints on the indicators. We show that a convex hull description of the associated mixed-integer set in an extended space with a quadratic number of additional variables consists of a single positive semidefinite constraint (explicitly stated) and linear constraints. In particular, convexification of this class of problems reduces to describing a polyhedral set in an extended formulation. We also give descriptions in the original space of variables: we provide a description based on an infinite number of conic-quadratic inequalities, which are "finitely generated." In particular, it is possible to characterize whether a given inequality is necessary to describe the convex-hull. The new theory presented here unifies several previously established results, and paves the way toward utilizing polyhedral methods to analyze the convex hull of mixed-integer nonlinear sets.

Safe Screening Rules for $\ell_0$-Regression

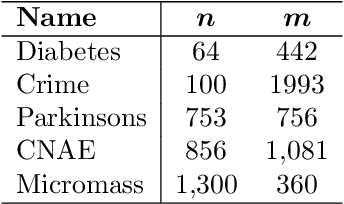
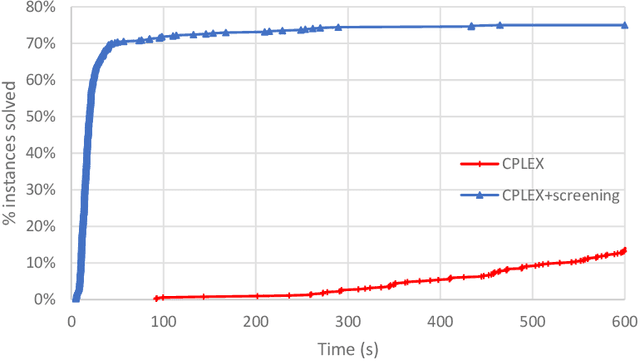
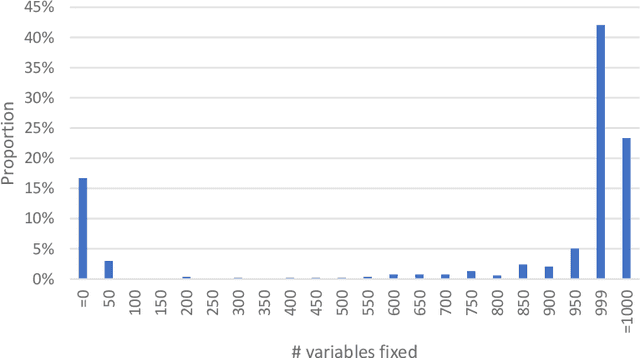
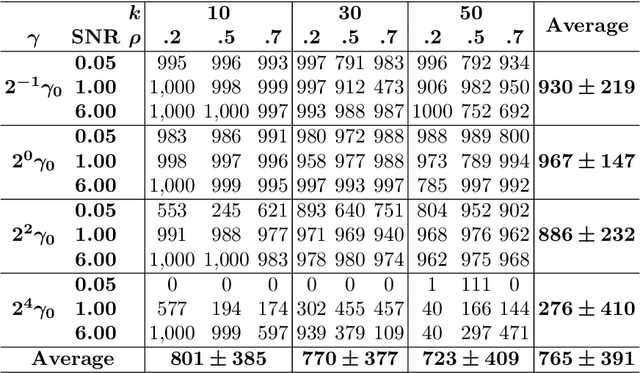
We give safe screening rules to eliminate variables from regression with $\ell_0$ regularization or cardinality constraint. These rules are based on guarantees that a feature may or may not be selected in an optimal solution. The screening rules can be computed from a convex relaxation solution in linear time, without solving the $\ell_0$ optimization problem. Thus, they can be used in a preprocessing step to safely remove variables from consideration apriori. Numerical experiments on real and synthetic data indicate that, on average, 76\% of the variables can be fixed to their optimal values, hence, reducing the computational burden for optimization substantially. Therefore, the proposed fast and effective screening rules extend the scope of algorithms for $\ell_0$-regression to larger data sets.