Ali H. Sayed
Enforcing Privacy in Distributed Learning with Performance Guarantees
Jan 16, 2023



Abstract:We study the privatization of distributed learning and optimization strategies. We focus on differential privacy schemes and study their effect on performance. We show that the popular additive random perturbation scheme degrades performance because it is not well-tuned to the graph structure. For this reason, we exploit two alternative graph-homomorphic constructions and show that they improve performance while guaranteeing privacy. Moreover, contrary to most earlier studies, the gradient of the risks is not assumed to be bounded (a condition that rarely holds in practice; e.g., quadratic risk). We avoid this condition and still devise a differentially private scheme with high probability. We examine optimization and learning scenarios and illustrate the theoretical findings through simulations.
Distributed Bayesian Learning of Dynamic States
Dec 05, 2022Abstract:This work studies networked agents cooperating to track a dynamical state of nature under partial information. The proposed algorithm is a distributed Bayesian filtering algorithm for finite-state hidden Markov models (HMMs). It can be used for sequential state estimation tasks, as well as for modeling opinion formation over social networks under dynamic environments. We show that the disagreement with the optimal centralized solution is asymptotically bounded for the class of geometrically ergodic state transition models, which includes rapidly changing models. We also derive recursions for calculating the probability of error and establish convergence under Gaussian observation models. Simulations are provided to illustrate the theory and to compare against alternative approaches.
Discovering Influencers in Opinion Formation over Social Graphs
Nov 23, 2022



Abstract:The adaptive social learning paradigm helps model how networked agents are able to form opinions on a state of nature and track its drifts in a changing environment. In this framework, the agents repeatedly update their beliefs based on private observations and exchange the beliefs with their neighbors. In this work, it is shown how the sequence of publicly exchanged beliefs over time allows users to discover rich information about the underlying network topology and about the flow of information over graph. In particular, it is shown that it is possible (i) to identify the influence of each individual agent to the objective of truth learning, (ii) to discover how well informed each agent is, (iii) to quantify the pairwise influences between agents, and (iv) to learn the underlying network topology. The algorithm derived herein is also able to work under non-stationary environments where either the true state of nature or the network topology are allowed to drift over time. We apply the proposed algorithm to different subnetworks of Twitter users, and identify the most influential and central agents merely by using their public tweets (posts).
Local Graph-homomorphic Processing for Privatized Distributed Systems
Oct 26, 2022Abstract:We study the generation of dependent random numbers in a distributed fashion in order to enable privatized distributed learning by networked agents. We propose a method that we refer to as local graph-homomorphic processing; it relies on the construction of particular noises over the edges to ensure a certain level of differential privacy. We show that the added noise does not affect the performance of the learned model. This is a significant improvement to previous works on differential privacy for distributed algorithms, where the noise was added in a less structured manner without respecting the graph topology and has often led to performance deterioration. We illustrate the theoretical results by considering a linear regression problem over a network of agents.
Networked Signal and Information Processing
Oct 25, 2022Abstract:The article reviews significant advances in networked signal and information processing, which have enabled in the last 25 years extending decision making and inference, optimization, control, and learning to the increasingly ubiquitous environments of distributed agents. As these interacting agents cooperate, new collective behaviors emerge from local decisions and actions. Moreover, and significantly, theory and applications show that networked agents, through cooperation and sharing, are able to match the performance of cloud or federated solutions, while preserving privacy, increasing resilience, and saving resources.
Quantization for decentralized learning under subspace constraints
Sep 16, 2022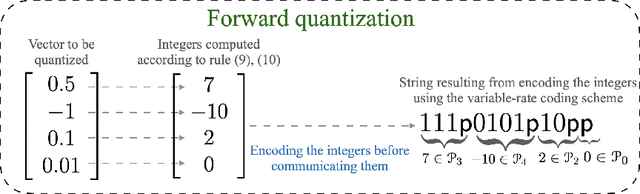
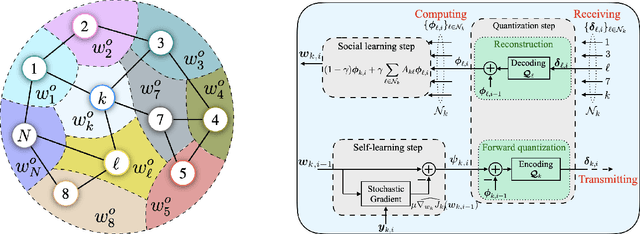
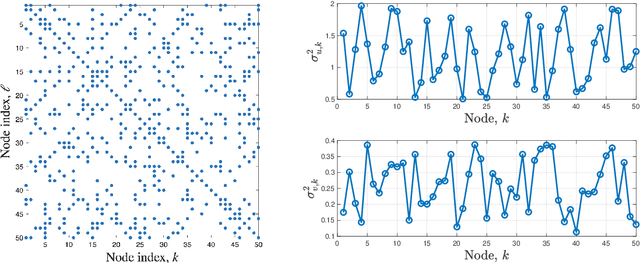
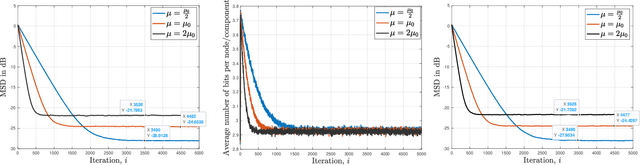
Abstract:In this paper, we consider decentralized optimization problems where agents have individual cost functions to minimize subject to subspace constraints that require the minimizers across the network to lie in low-dimensional subspaces. This constrained formulation includes consensus or single-task optimization as special cases, and allows for more general task relatedness models such as multitask smoothness and coupled optimization. In order to cope with communication constraints, we propose and study an adaptive decentralized strategy where the agents employ differential randomized quantizers to compress their estimates before communicating with their neighbors. The analysis shows that, under some general conditions on the quantization noise, and for sufficiently small step-sizes $\mu$, the strategy is stable both in terms of mean-square error and average bit rate: by reducing $\mu$, it is possible to keep the estimation errors small (on the order of $\mu$) without increasing indefinitely the bit rate as $\mu\rightarrow 0$. Simulations illustrate the theoretical findings and the effectiveness of the proposed approach, revealing that decentralized learning is achievable at the expense of only a few bits.
A Fundamental Limit of Distributed Hypothesis Testing Under Memoryless Quantization
Jun 24, 2022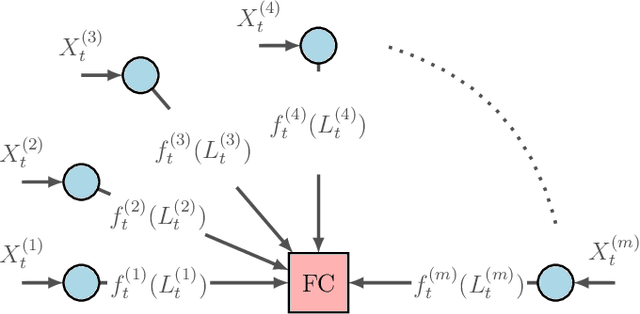
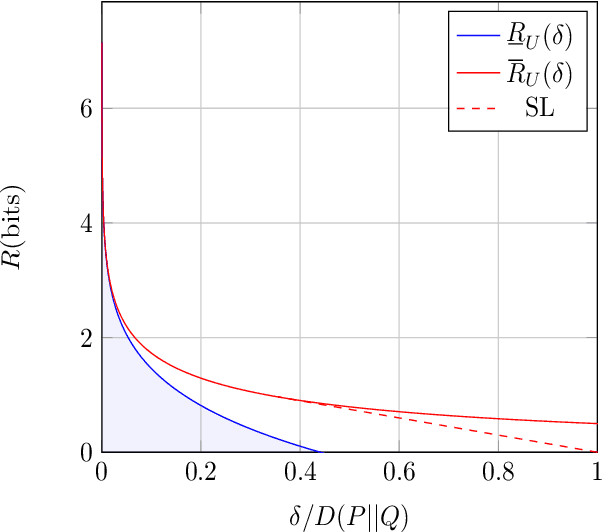

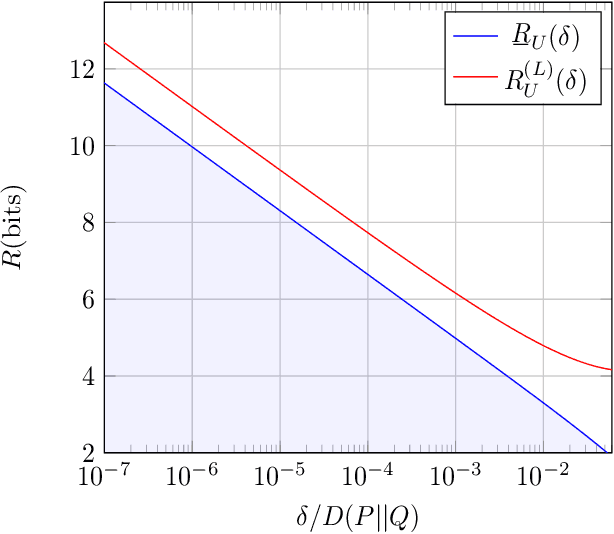
Abstract:We study a distributed hypothesis testing setup where peripheral nodes send quantized data to the fusion center in a memoryless fashion. The \emph{expected} number of bits sent by each node under the null hypothesis is kept limited. We characterize the optimal decay rate of the mis-detection (type-II error) probability provided that false alarms (type-I error) are rare, and study the tradeoff between the communication rate and maximal type-II error decay rate. We resort to rate-distortion methods to provide upper bounds to the tradeoff curve and show that at high rates lattice quantization achieves near-optimal performance. We also characterize the tradeoff for the case where nodes are allowed to record and quantize a fixed number of samples. Moreover, under sum-rate constraints, we show that an upper bound to the tradeoff curve is obtained with a water-filling solution.
On the Arithmetic and Geometric Fusion of Beliefs for Distributed Inference
Apr 28, 2022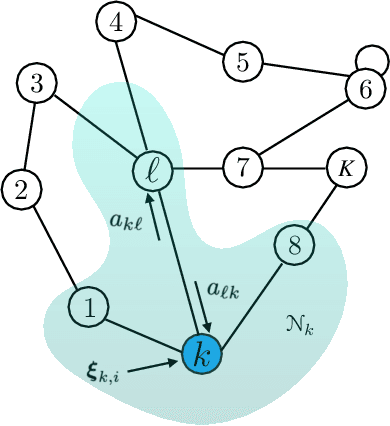
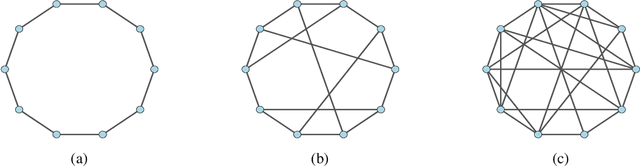
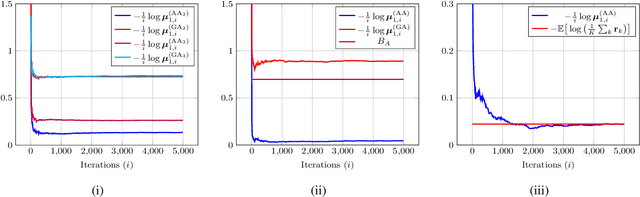
Abstract:We study the asymptotic learning rates under linear and log-linear combination rules of belief vectors in a distributed hypothesis testing problem. We show that under both combination strategies, agents are able to learn the truth exponentially fast, with a faster rate under log-linear fusion. We examine the gap between the rates in terms of network connectivity and information diversity. We also provide closed-form expressions for special cases involving federated architectures and exchangeable networks.
Dencentralized learning in the presence of low-rank noise
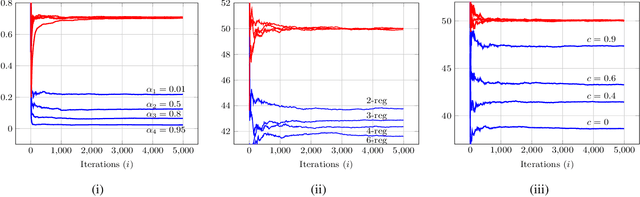
Mar 18, 2022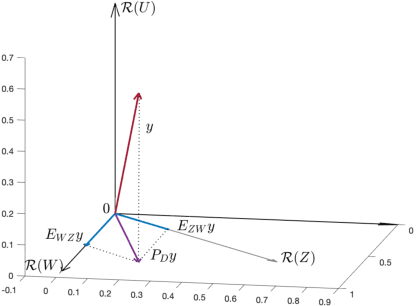
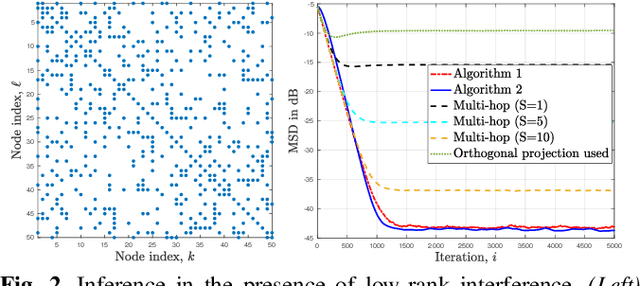
Abstract:Observations collected by agents in a network may be unreliable due to observation noise or interference. This paper proposes a distributed algorithm that allows each node to improve the reliability of its own observation by relying solely on local computations and interactions with immediate neighbors, assuming that the field (graph signal) monitored by the network lies in a low-dimensional subspace and that a low-rank noise is present in addition to the usual full-rank noise. While oblique projections can be used to project measurements onto a low-rank subspace along a direction that is oblique to the subspace, the resulting solution is not distributed. Starting from the centralized solution, we propose an algorithm that performs the oblique projection of the overall set of observations onto the signal subspace in an iterative and distributed manner. We then show how the oblique projection framework can be extended to handle distributed learning and adaptation problems over networks.
Explainability and Graph Learning from Social Interactions
Mar 14, 2022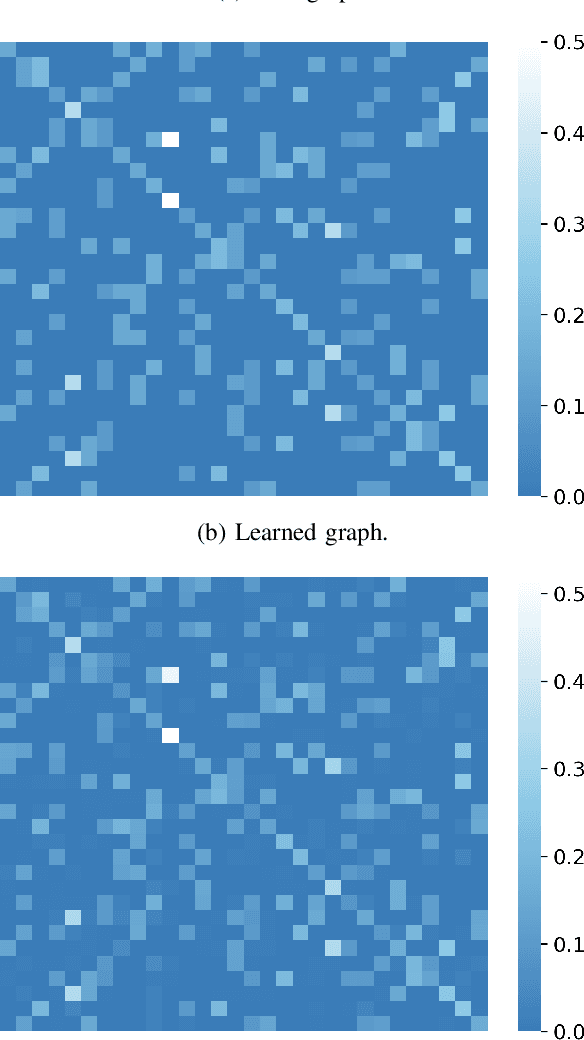
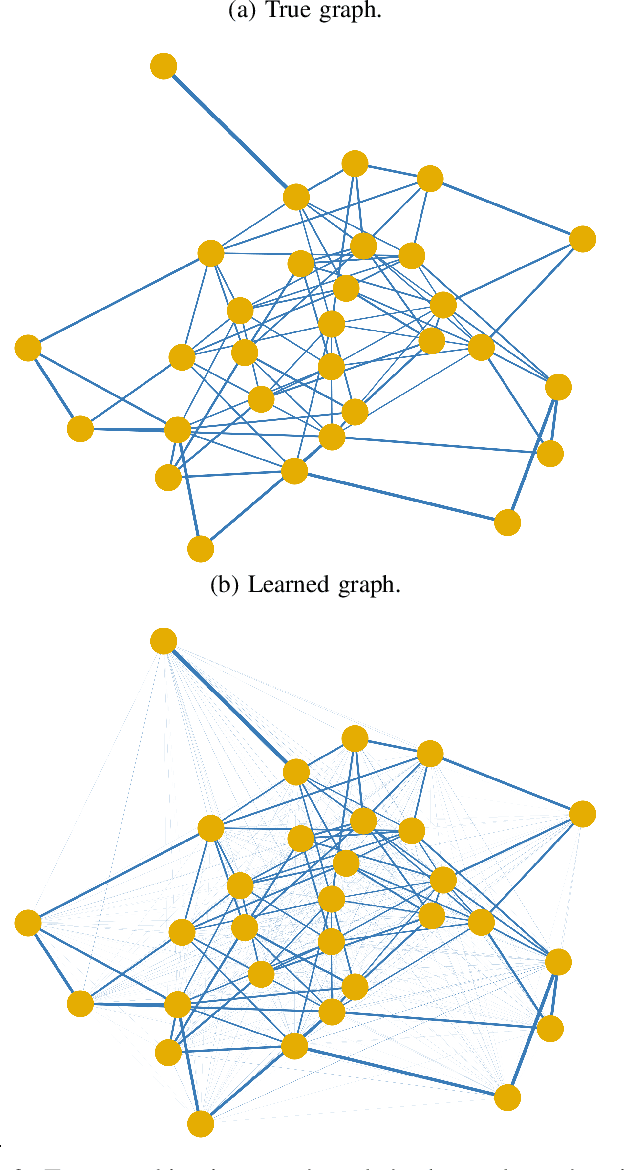
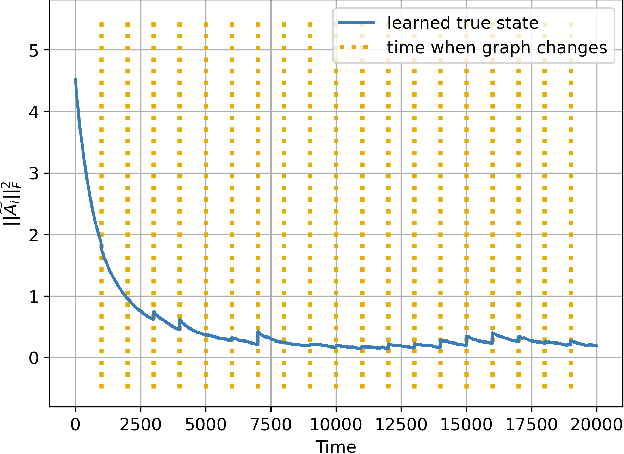
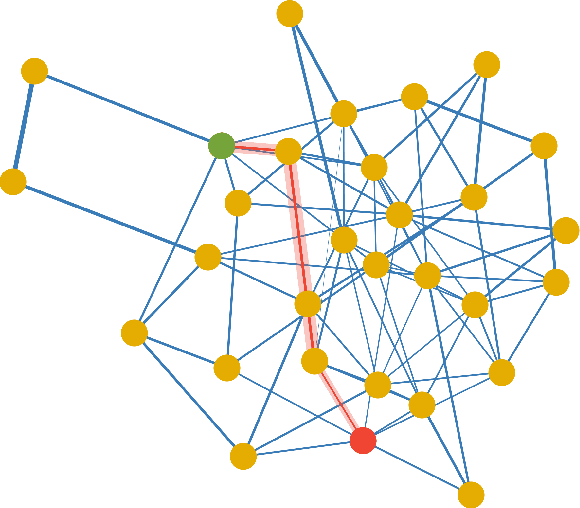
Abstract:Social learning algorithms provide models for the formation of opinions over social networks resulting from local reasoning and peer-to-peer exchanges. Interactions occur over an underlying graph topology, which describes the flow of information among the agents. In this work, we propose a technique that addresses questions of explainability and interpretability when the graph is hidden. Given observations of the evolution of the belief over time, we aim to infer the underlying graph topology, discover pairwise influences between the agents, and identify significant trajectories in the network. The proposed framework is online in nature and can adapt dynamically to changes in the graph topology or the true hypothesis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge