Mixed neural network Gaussian processes

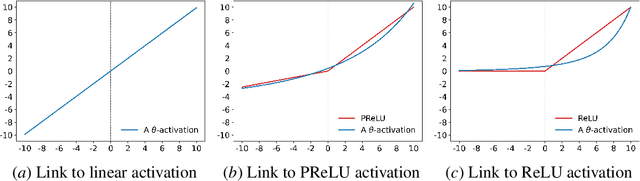
This paper makes two contributions. Firstly, it introduces mixed compositional kernels and mixed neural network Gaussian processes (NGGPs). Mixed compositional kernels are generated by composition of probability generating functions (PGFs). A mixed NNGP is a Gaussian process (GP) with a mixed compositional kernel, arising in the infinite-width limit of multilayer perceptrons (MLPs) that have a different activation function for each layer. Secondly, $\theta$ activation functions for neural networks and $\theta$ compositional kernels are introduced by building upon the theory of branching processes, and more specifically upon $\theta$ PGFs. While $\theta$ compositional kernels are recursive, they are expressed in closed form. It is shown that $\theta$ compositional kernels have non-degenerate asymptotic properties under certain conditions. Thus, GPs with $\theta$ compositional kernels do not require non-explicit recursive kernel evaluations and have controllable infinite-depth asymptotic properties. An open research question is whether GPs with $\theta$ compositional kernels are limits of infinitely-wide MLPs with $\theta$ activation functions.

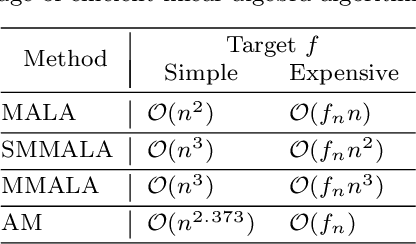
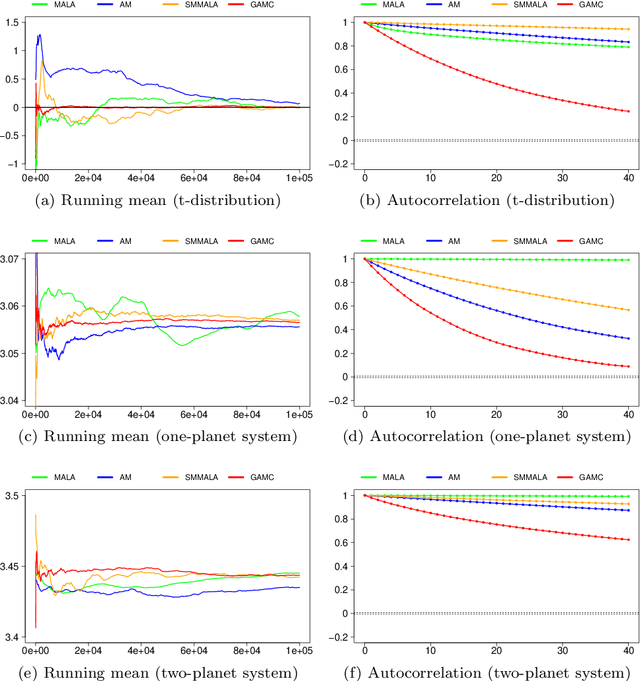
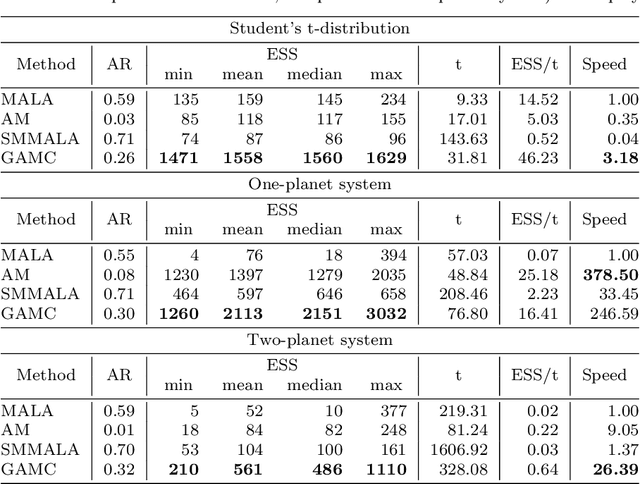
Geometric adaptive Monte Carlo in random environment

Manifold Markov chain Monte Carlo algorithms have been introduced to sample more effectively from challenging target densities exhibiting multiple modes or strong correlations. Such algorithms exploit the local geometry of the parameter space, thus enabling chains to achieve a faster convergence rate when measured in number of steps. However, acquiring local geometric information can often increase computational complexity per step to the extent that sampling from high-dimensional targets becomes inefficient in terms of total computational time. This paper analyzes the computational complexity of manifold Langevin Monte Carlo and proposes a geometric adaptive Monte Carlo sampler aimed at balancing the benefits of exploiting local geometry with computational cost to achieve a high effective sample size for a given computational cost. The suggested sampler is a discrete-time stochastic process in random environment. The random environment allows to switch between local geometric and adaptive proposal kernels with the help of a schedule. An exponential schedule is put forward that enables more frequent use of geometric information in early transient phases of the chain, while saving computational time in late stationary phases. The average complexity can be manually set depending on the need for geometric exploitation posed by the underlying model.