Coreset selection for the Sinkhorn divergence and generic smooth divergences

We introduce CO2, an efficient algorithm to produce convexly-weighted coresets with respect to generic smooth divergences. By employing a functional Taylor expansion, we show a local equivalence between sufficiently regular losses and their second order approximations, reducing the coreset selection problem to maximum mean discrepancy minimization. We apply CO2 to the Sinkhorn divergence, providing a novel sampling procedure that requires logarithmically many data points to match the approximation guarantees of random sampling. To show this, we additionally verify several new regularity properties for entropically regularized optimal transport of independent interest. Our approach leads to a new perspective linking coreset selection and kernel quadrature to classical statistical methods such as moment and score matching. We showcase this method with a practical application of subsampling image data, and highlight key directions to explore for improved algorithmic efficiency and theoretical guarantees.

Euclidean and Affine Curve Reconstruction

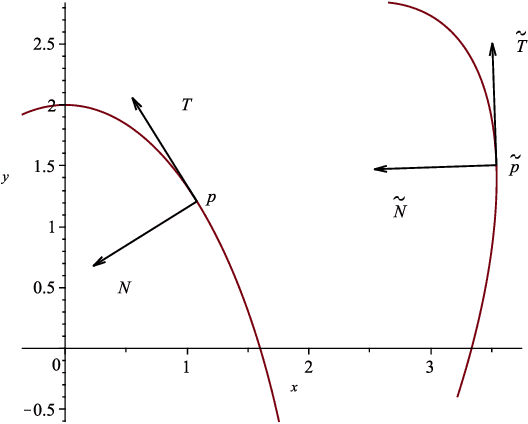
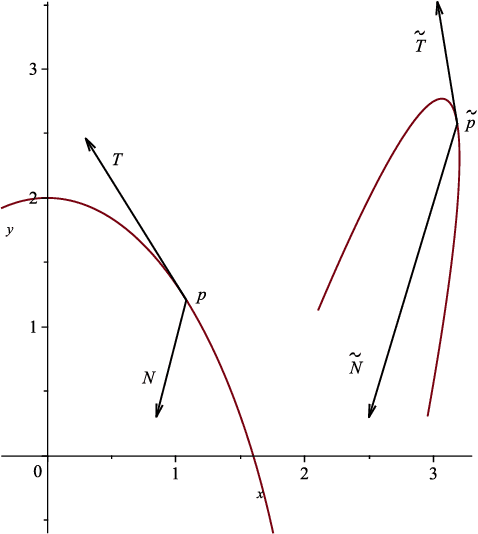
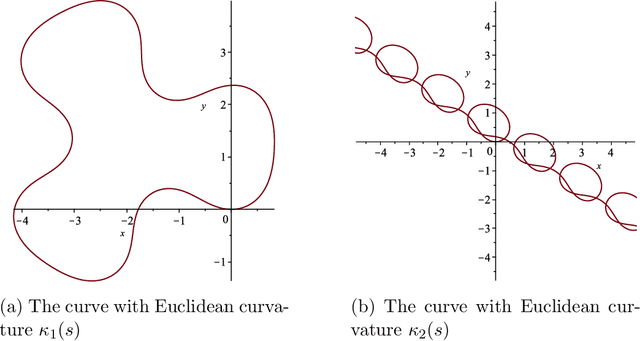
We consider practical aspects of reconstructing planar curves with prescribed Euclidean or affine curvatures. These curvatures are invariant under the special Euclidean group and the equi-affine groups, respectively, and play an important role in computer vision and shape analysis. We discuss and implement algorithms for such reconstruction, and give estimates on how close reconstructed curves are relative to the closeness of their curvatures in appropriate metrics. Several illustrative examples are provided.