Sequential Transfer in Multi-armed Bandit with Finite Set of Models

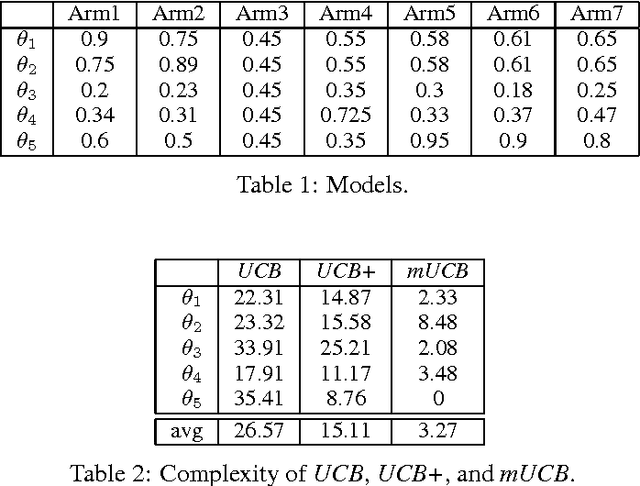
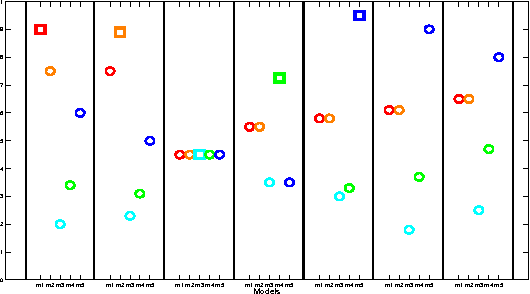
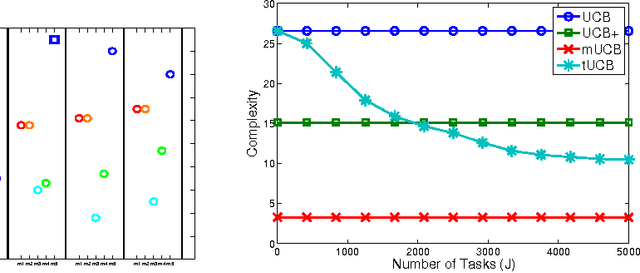
Learning from prior tasks and transferring that experience to improve future performance is critical for building lifelong learning agents. Although results in supervised and reinforcement learning show that transfer may significantly improve the learning performance, most of the literature on transfer is focused on batch learning tasks. In this paper we study the problem of \textit{sequential transfer in online learning}, notably in the multi-armed bandit framework, where the objective is to minimize the cumulative regret over a sequence of tasks by incrementally transferring knowledge from prior tasks. We introduce a novel bandit algorithm based on a method-of-moments approach for the estimation of the possible tasks and derive regret bounds for it.

Regret Bounds for Reinforcement Learning with Policy Advice

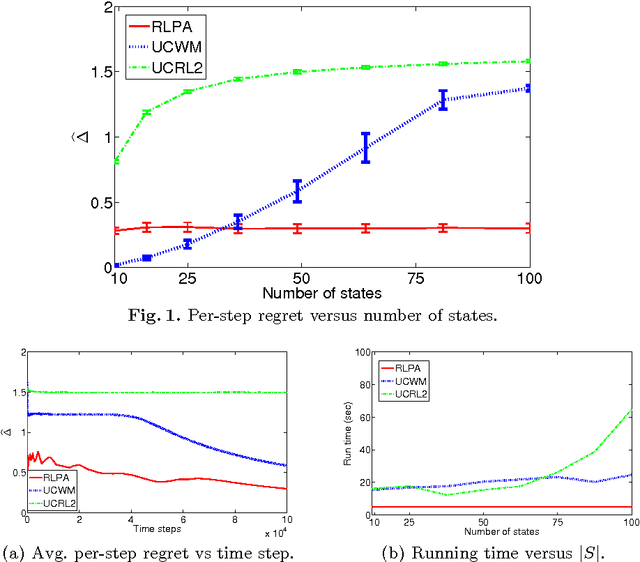
In some reinforcement learning problems an agent may be provided with a set of input policies, perhaps learned from prior experience or provided by advisors. We present a reinforcement learning with policy advice (RLPA) algorithm which leverages this input set and learns to use the best policy in the set for the reinforcement learning task at hand. We prove that RLPA has a sub-linear regret of \tilde O(\sqrt{T}) relative to the best input policy, and that both this regret and its computational complexity are independent of the size of the state and action space. Our empirical simulations support our theoretical analysis. This suggests RLPA may offer significant advantages in large domains where some prior good policies are provided.

Risk-Aversion in Multi-armed Bandits

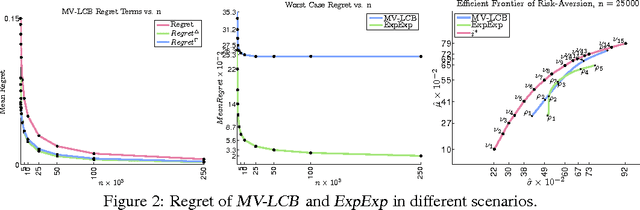
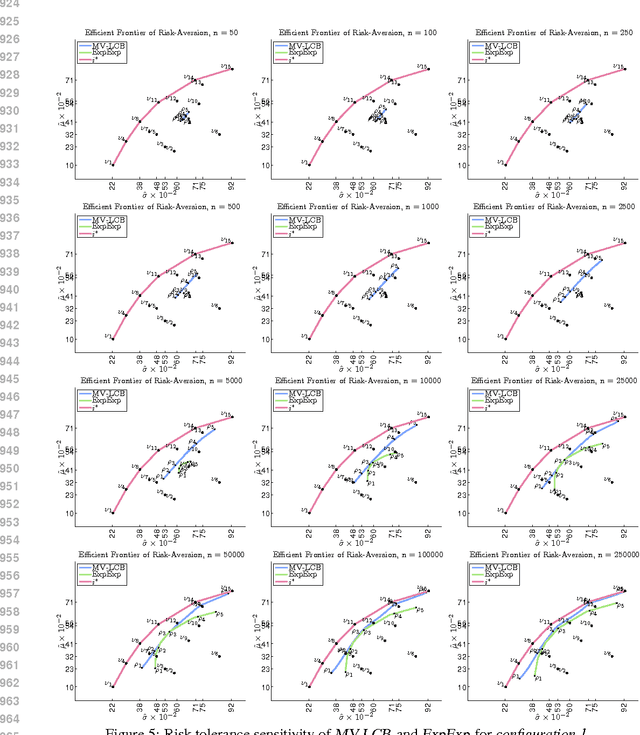
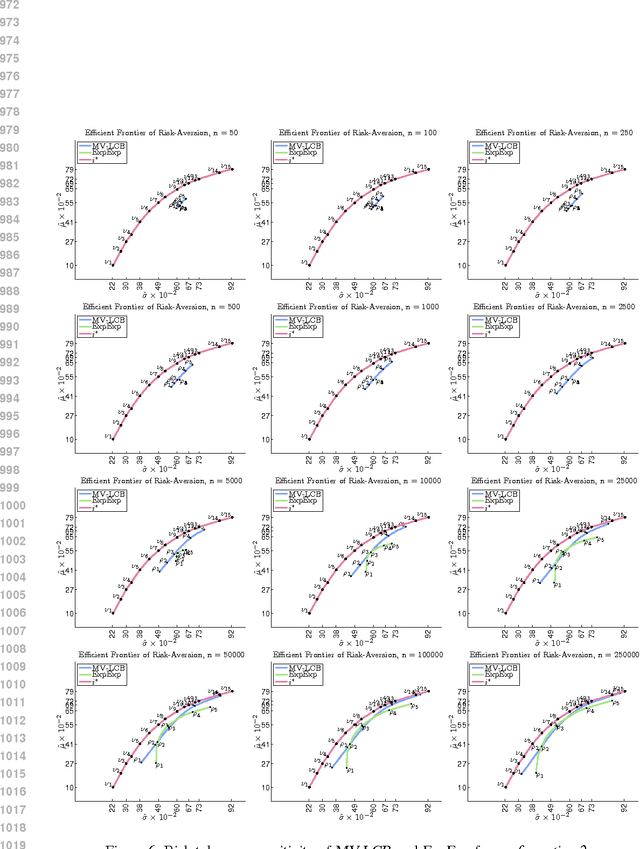
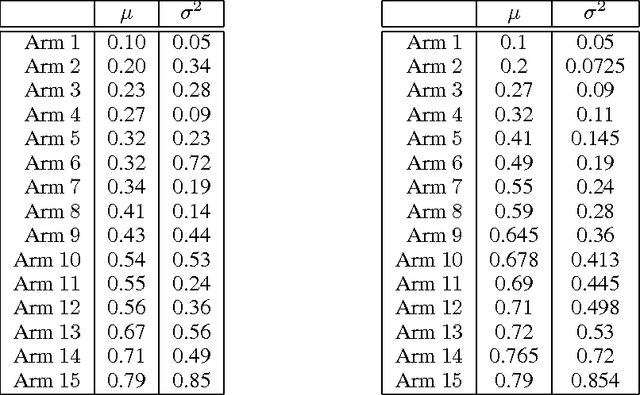
Stochastic multi-armed bandits solve the Exploration-Exploitation dilemma and ultimately maximize the expected reward. Nonetheless, in many practical problems, maximizing the expected reward is not the most desirable objective. In this paper, we introduce a novel setting based on the principle of risk-aversion where the objective is to compete against the arm with the best risk-return trade-off. This setting proves to be intrinsically more difficult than the standard multi-arm bandit setting due in part to an exploration risk which introduces a regret associated to the variability of an algorithm. Using variance as a measure of risk, we introduce two new algorithms, investigate their theoretical guarantees, and report preliminary empirical results.

A Dantzig Selector Approach to Temporal Difference Learning

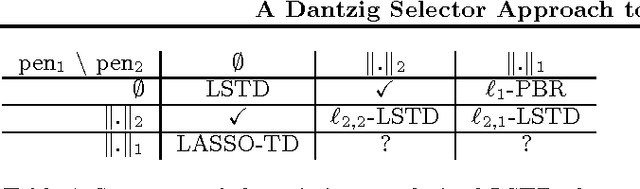
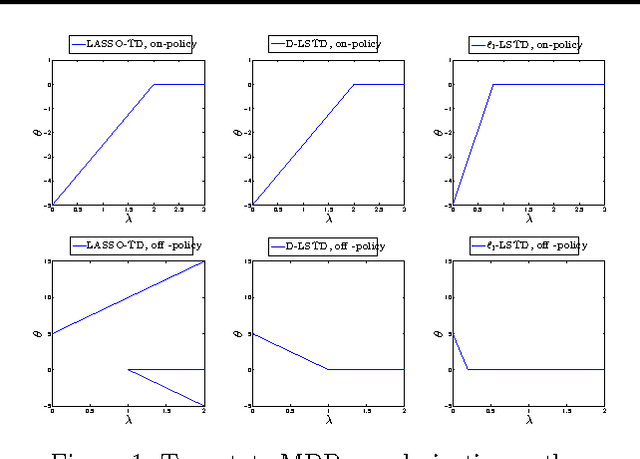
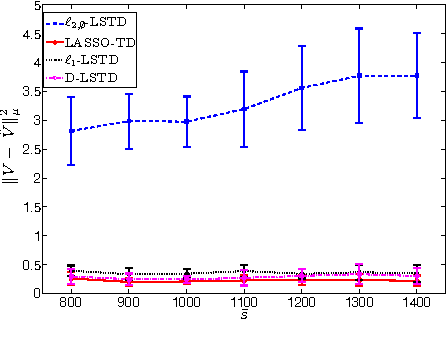
LSTD is a popular algorithm for value function approximation. Whenever the number of features is larger than the number of samples, it must be paired with some form of regularization. In particular, L1-regularization methods tend to perform feature selection by promoting sparsity, and thus, are well-suited for high-dimensional problems. However, since LSTD is not a simple regression algorithm, but it solves a fixed--point problem, its integration with L1-regularization is not straightforward and might come with some drawbacks (e.g., the P-matrix assumption for LASSO-TD). In this paper, we introduce a novel algorithm obtained by integrating LSTD with the Dantzig Selector. We investigate the performance of the proposed algorithm and its relationship with the existing regularized approaches, and show how it addresses some of their drawbacks.

Transfer from Multiple MDPs

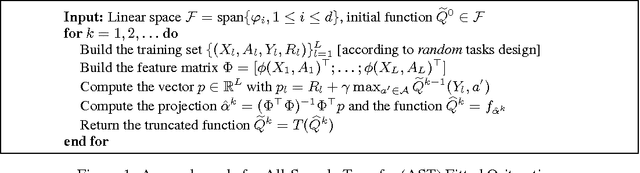
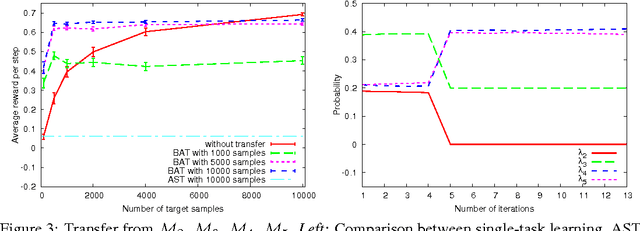
Transfer reinforcement learning (RL) methods leverage on the experience collected on a set of source tasks to speed-up RL algorithms. A simple and effective approach is to transfer samples from source tasks and include them into the training set used to solve a given target task. In this paper, we investigate the theoretical properties of this transfer method and we introduce novel algorithms adapting the transfer process on the basis of the similarity between source and target tasks. Finally, we report illustrative experimental results in a continuous chain problem.