Attention with Trained Embeddings Provably Selects Important Tokens

Token embeddings play a crucial role in language modeling but, despite this practical relevance, their theoretical understanding remains limited. Our paper addresses the gap by characterizing the structure of embeddings obtained via gradient descent. Specifically, we consider a one-layer softmax attention model with a linear head for binary classification, i.e., $\texttt{Softmax}( p^\top E_X^\top ) E_X v = \frac{ \sum_{i=1}^T \exp(p^\top E_{x_i}) E_{x_i}^\top v}{\sum_{j=1}^T \exp(p^\top E_{x_{j}}) }$, where $E_X = [ E_{x_1} , \dots, E_{x_T} ]^\top$ contains the embeddings of the input sequence, $p$ is the embedding of the $\mathrm{\langle cls \rangle}$ token and $v$ the output vector. First, we show that, already after a single step of gradient training with the logistic loss, the embeddings $E_X$ capture the importance of tokens in the dataset by aligning with the output vector $v$ proportionally to the frequency with which the corresponding tokens appear in the dataset. Then, after training $p$ via gradient flow until convergence, the softmax selects the important tokens in the sentence (i.e., those that are predictive of the label), and the resulting $\mathrm{\langle cls \rangle}$ embedding maximizes the margin for such a selection. Experiments on real-world datasets (IMDB, Yelp) exhibit a phenomenology close to that unveiled by our theory.

Scaling Matters in Deep Structured-Prediction Models

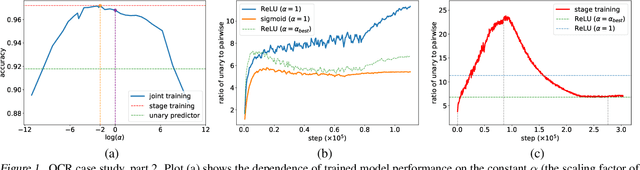
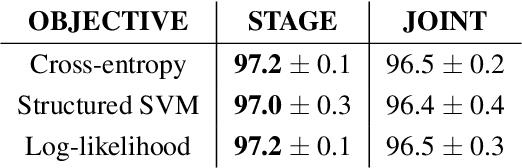
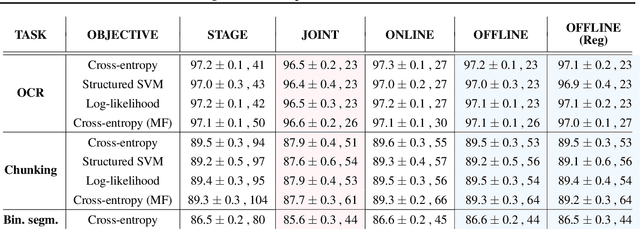
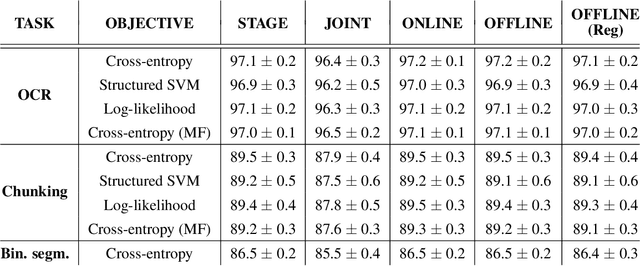
Deep structured-prediction energy-based models combine the expressive power of learned representations and the ability of embedding knowledge about the task at hand into the system. A common way to learn parameters of such models consists in a multistage procedure where different combinations of components are trained at different stages. The joint end-to-end training of the whole system is then done as the last fine-tuning stage. This multistage approach is time-consuming and cumbersome as it requires multiple runs until convergence and multiple rounds of hyperparameter tuning. From this point of view, it is beneficial to start the joint training procedure from the beginning. However, such approaches often unexpectedly fail and deliver results worse than the multistage ones. In this paper, we hypothesize that one reason for joint training of deep energy-based models to fail is the incorrect relative normalization of different components in the energy function. We propose online and offline scaling algorithms that fix the joint training and demonstrate their efficacy on three different tasks.