TabularQGAN: A Quantum Generative Model for Tabular Data

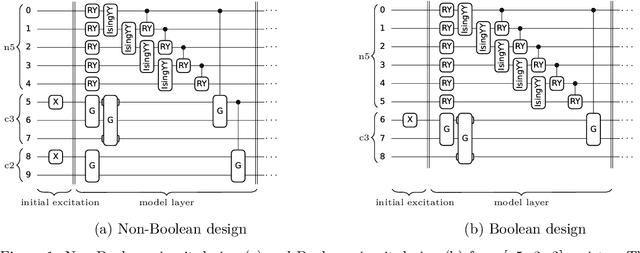
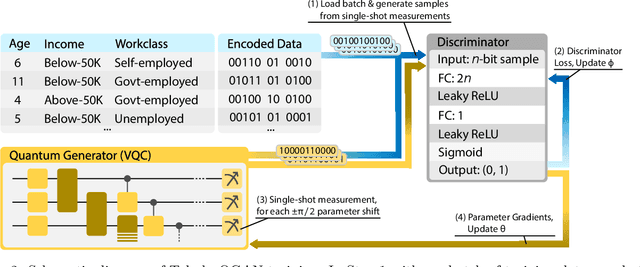
In this paper, we introduce a novel quantum generative model for synthesizing tabular data. Synthetic data is valuable in scenarios where real-world data is scarce or private, it can be used to augment or replace existing datasets. Real-world enterprise data is predominantly tabular and heterogeneous, often comprising a mixture of categorical and numerical features, making it highly relevant across various industries such as healthcare, finance, and software. We propose a quantum generative adversarial network architecture with flexible data encoding and a novel quantum circuit ansatz to effectively model tabular data. The proposed approach is tested on the MIMIC III healthcare and Adult Census datasets, with extensive benchmarking against leading classical models, CTGAN, and CopulaGAN. Experimental results demonstrate that our quantum model outperforms classical models by an average of 8.5% with respect to an overall similarity score from SDMetrics, while using only 0.072% of the parameters of the classical models. Additionally, we evaluate the generalization capabilities of the models using two custom-designed metrics that demonstrate the ability of the proposed quantum model to generate useful and novel samples. To our knowledge, this is one of the first demonstrations of a successful quantum generative model for handling tabular data, indicating that this task could be well-suited to quantum computers.

Unsupervised Learning of Invariance Transformations

The need for large amounts of training data in modern machine learning is one of the biggest challenges of the field. Compared to the brain, current artificial algorithms are much less capable of learning invariance transformations and employing them to extrapolate knowledge from small sample sets. It has recently been proposed that the brain might encode perceptual invariances as approximate graph symmetries in the network of synaptic connections. Such symmetries may arise naturally through a biologically plausible process of unsupervised Hebbian learning. In the present paper, we illustrate this proposal on numerical examples, showing that invariance transformations can indeed be recovered from the structure of recurrent synaptic connections which form within a layer of feature detector neurons via a simple Hebbian learning rule. In order to numerically recover the invariance transformations from the resulting recurrent network, we develop a general algorithmic framework for finding approximate graph automorphisms. We discuss how this framework can be used to find approximate automorphisms in weighted graphs in general.