A Generalization of the Convolution Theorem and its Connections to Non-Stationarity and the Graph Frequency Domain

In this paper, we present a novel convolution theorem which encompasses the well known convolution theorem in (graph) signal processing as well as the one related to time-varying filters. Specifically, we show how a node-wise convolution for signals supported on a graph can be expressed as another node-wise convolution in a frequency domain graph, different from the original graph. This is achieved through a parameterization of the filter coefficients following a basis expansion model. After showing how the presented theorem is consistent with the already existing body of literature, we discuss its implications in terms of non-stationarity. Finally, we propose a data-driven algorithm based on subspace fitting to learn the frequency domain graph, which is then corroborated by experimental results on synthetic and real data.

Forecasting Graph Signals with Recursive MIMO Graph Filters

Forecasting time series on graphs is a fundamental problem in graph signal processing. When each entity of the network carries a vector of values for each time stamp instead of a scalar one, existing approaches resort to the use of product graphs to combine this multidimensional information, at the expense of creating a larger graph. In this paper, we show the limitations of such approaches, and propose extensions to tackle them. Then, we propose a recursive multiple-input multiple-output graph filter which encompasses many already existing models in the literature while being more flexible. Numerical simulations on a real world data set show the effectiveness of the proposed models.

Learning Time-Varying Graphs from Online Data

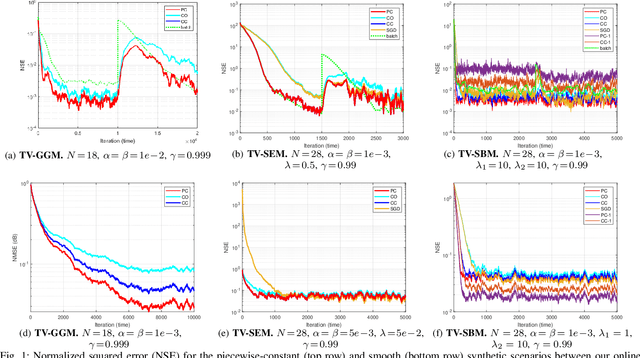
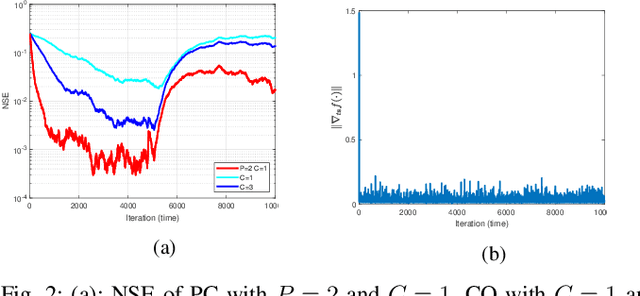
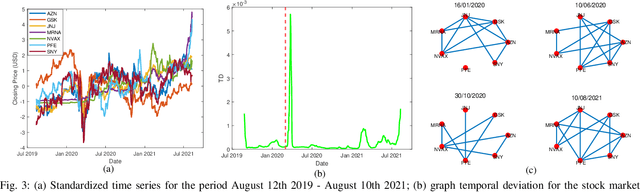
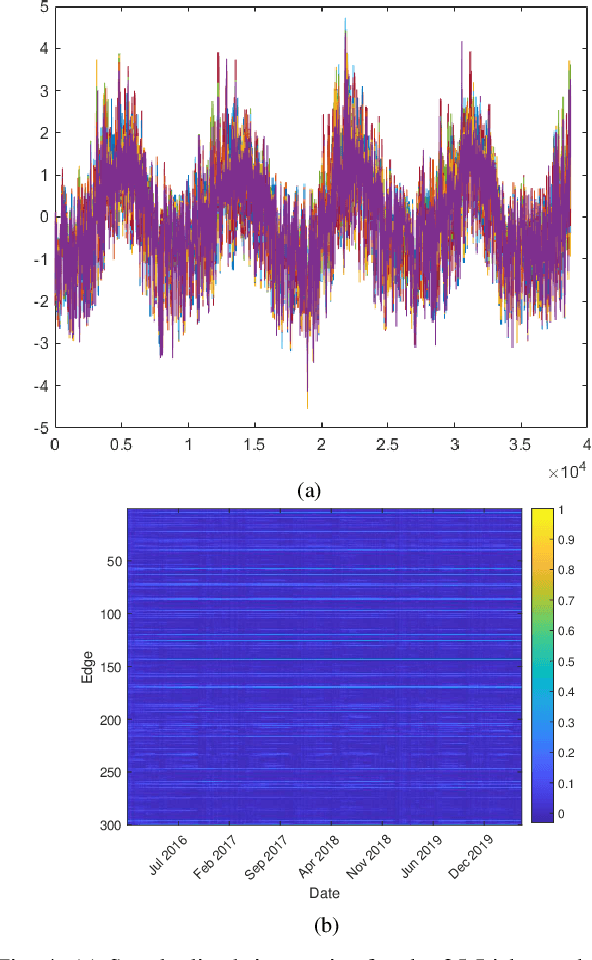
This work proposes an algorithmic framework to learn time-varying graphs from online data. The generality offered by the framework renders it model-independent, i.e., it can be theoretically analyzed in its abstract formulation and then instantiated under a variety of model-dependent graph learning problems. This is possible by phrasing (time-varying) graph learning as a composite optimization problem, where different functions regulate different desiderata, e.g., data fidelity, sparsity or smoothness. Instrumental for the findings is recognizing that the dependence of the majority (if not all) data-driven graph learning algorithms on the data is exerted through the empirical covariance matrix, representing a sufficient statistic for the estimation problem. Its user-defined recursive update enables the framework to work in non-stationary environments, while iterative algorithms building on novel time-varying optimization tools explicitly take into account the temporal dynamics, speeding up convergence and implicitly including a temporal-regularization of the solution. We specialize the framework to three well-known graph learning models, namely, the Gaussian graphical model (GGM), the structural equation model (SEM), and the smoothness-based model (SBM), where we also introduce ad-hoc vectorization schemes for structured matrices (symmetric, hollows, etc.) which are crucial to perform correct gradient computations, other than enabling to work in low-dimensional vector spaces and hence easing storage requirements. After discussing the theoretical guarantees of the proposed framework, we corroborate it with extensive numerical tests in synthetic and real data.

Online Time-Varying Topology Identification via Prediction-Correction Algorithms

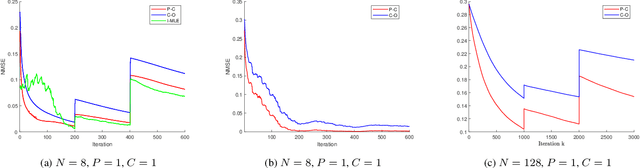
Signal processing and machine learning algorithms for data supported over graphs, require the knowledge of the graph topology. Unless this information is given by the physics of the problem (e.g., water supply networks, power grids), the topology has to be learned from data. Topology identification is a challenging task, as the problem is often ill-posed, and becomes even harder when the graph structure is time-varying. In this paper, we address the problem of dynamic topology identification by building on recent results from time-varying optimization, devising a general-purpose online algorithm operating in non-stationary environments. Because of its iteration-constrained nature, the proposed approach exhibits an intrinsic temporal-regularization of the graph topology without explicitly enforcing it. As a case-study, we specialize our method to the Gaussian graphical model (GGM) problem and corroborate its performance.

Forecasting Multi-Dimensional Processes over Graphs

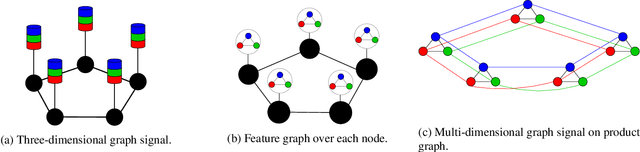
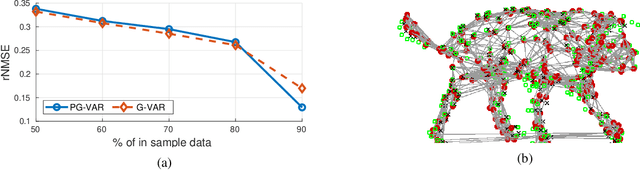
The forecasting of multi-variate time processes through graph-based techniques has recently been addressed under the graph signal processing framework. However, problems in the representation and the processing arise when each time series carries a vector of quantities rather than a scalar one. To tackle this issue, we devise a new framework and propose new methodologies based on the graph vector autoregressive model. More explicitly, we leverage product graphs to model the high-dimensional graph data and develop multi-dimensional graph-based vector autoregressive models to forecast future trends with a number of parameters that is independent of the number of time series and a linear computational complexity. Numerical results demonstrating the prediction of moving point clouds corroborate our findings.