Aicha Baya Goumeidane
Linear Anchored Gaussian Mixture Model for Location and Width Computation of Objects in Thick Line Shape
Apr 07, 2024Abstract:An accurate detection of the centerlines of linear objects is a challenging topic in many sensitive real-world applications such X-ray imaging, remote sensing and lane marking detection in road traffic. Model-based approaches using Hough and Radon transforms are often used but, are not recommended for thick line detection, whereas approaches based on image derivatives need further step-by-step processing, making their efficiency dependent on each step outcomes. In this paper, we aim to detect linear structures found in images by considering the 3D representation of the image gray levels as a finite mixture model of statistical distribution. The latter, which we named linear anchored Gaussian distribution could be parametrized by a scale value ${\sigma}$ describing the linear structure thickness and a line equation, parametrized, in turn, by a radius ${\rho}$ and an orientation angle ${\theta}$, describing the linear structure centerline location. Expectation-Maximization (EM) algorithm is used for the mixture model parameter estimation, where a new paradigm, using the background subtraction for the likelihood function computation, is proposed. For the EM algorithm, two ${\theta}$ parameter initialization schemes are used: the first one is based on a random choice of the first component of ${\theta}$ vector, whereas the second is based on the image Hessian with a simultaneous computation of the mixture model components number. Experiments on real world images and synthetic images corrupted by blur and additive noise show the good performance of the proposed methods, where the algorithm using background subtraction and Hessian-based ${\theta}$ initialization provides an outstanding accuracy of the linear structure detection despite irregular image background and presence of blur and noise.
Guided Scale Space Radon Transform for linear structures detection
Nov 15, 2023Abstract:Using integral transforms to the end of lines detection in images with complex background, makes the detection a hard task needing additional processing to manage the detection. As an integral transform, the Scale Space Radon Transform (SSRT) suffers from such drawbacks, even with its great abilities for thick lines detection. In this work, we propose a method to address this issue for automatic detection of thick linear structures in gray scale and binary images using the SSRT, whatever the image background content. This method involves the calculated Hessian orientations of the investigated image while computing its SSRT, in such a way that linear structures are emphasized in the SSRT space. As a consequence, the subsequent maxima detection in the SSRT space is done on a modified transform space freed from unwanted parts and, consequently, from irrelevant peaks that usually drown the peaks representing lines. Besides, highlighting the linear structure in the SSRT space permitting, thus, to efficiently detect lines of different thickness in synthetic and real images, the experiments show also the method robustness against noise and complex background.
Scale space radon transform-based inertia axis and object central symmetry estimation
Mar 22, 2023Abstract:Inertia Axes are involved in many techniques for image content measurement when involving information obtained from lines, angles, centroids... etc. We investigate, here, the estimation of the main axis of inertia of an object in the image. We identify the coincidence conditions of the Scale Space Radon Transform (SSRT) maximum and the inertia main axis. We show, that by choosing the appropriate scale parameter, it is possible to match the SSRT maximum and the main axis of inertia location and orientation of the embedded object in the image. Furthermore, an example of use case is presented where binary objects central symmetry computation is derived by means of SSRT projections and the axis of inertia orientation. To this end, some SSRT characteristics have been highlighted and exploited. The experimentations show the SSRT-based main axis of inertia computation effectiveness. Concerning the central symmetry, results are very satisfying as experimentations carried out on randomly created images dataset and existing datasets have permitted to divide successfully these images bases into centrally symmetric and non-centrally symmetric objects.
On Scale Space Radon Transform, Properties and Image Reconstruction
May 10, 2022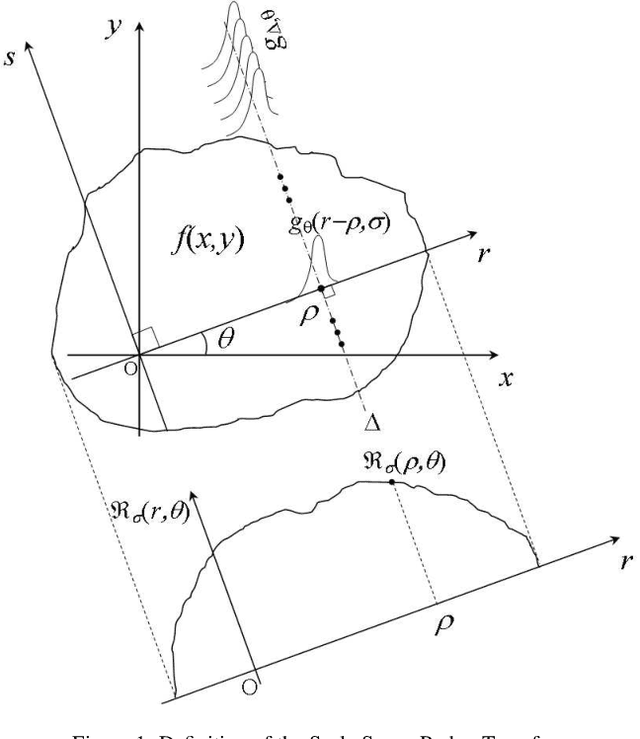
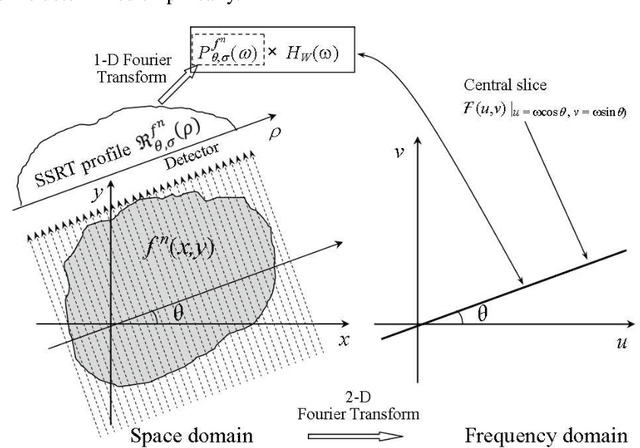
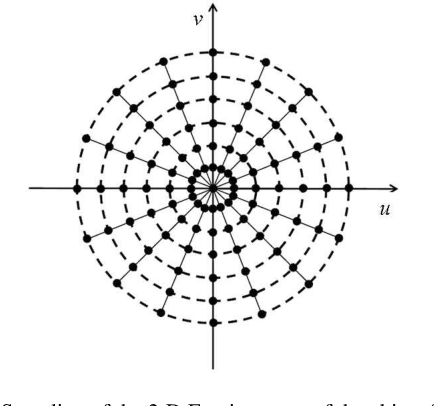
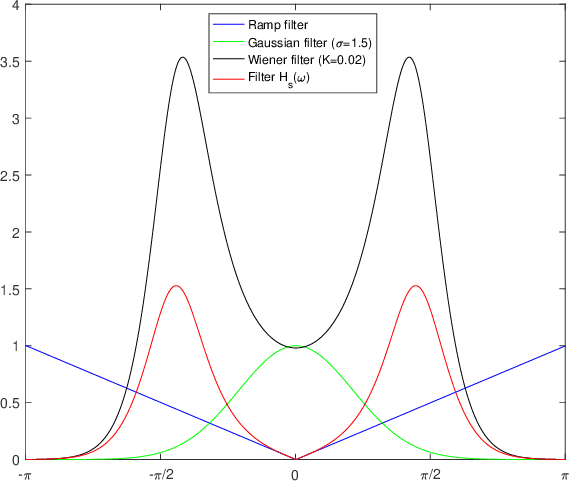
Abstract:Aware of the importance of the good behavior in the scale space that a mathematical transform must have, we depict, in this paper, the basic properties and the inverse transform of the Scale Space Radon Transform (SSRT). To reconstruct the image from SSRT sinogram, the Filtered backprojection (FBP) technique is used in two different ways: (1) Deconvolve SSRT to obtain the estimated Radon transform (RT) and then, reconstruct image using classical FBP or (2) Adapt FBP technique to SSRT so that the Radon projections spectrum used in classical FBP is replaced by SSRT and Wiener filtering, expressed in the frequency domain. Comparison of image reconstruction techniques using SSRT and RT are performed on Shepp-Logan head phantom image. Using the Mean Absolute Error (MAE) as image reconstruction quality measure, the preliminary results present an outstanding performance for SSRT-based image reconstruction techniques compared to the RT-based one. Furthermore, the method (2) outperforms the method (1) in terms of computation time and adaptability for high level of noise when fairly large Gaussian kernel is used.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge