NeurIPS 2024 ML4CFD Competition: Results and Retrospective Analysis

The integration of machine learning (ML) into the physical sciences is reshaping computational paradigms, offering the potential to accelerate demanding simulations such as computational fluid dynamics (CFD). Yet, persistent challenges in accuracy, generalization, and physical consistency hinder the practical deployment of ML models in scientific domains. To address these limitations and systematically benchmark progress, we organized the ML4CFD competition, centered on surrogate modeling for aerodynamic simulations over two-dimensional airfoils. The competition attracted over 240 teams, who were provided with a curated dataset generated via OpenFOAM and evaluated through a multi-criteria framework encompassing predictive accuracy, physical fidelity, computational efficiency, and out-of-distribution generalization. This retrospective analysis reviews the competition outcomes, highlighting several approaches that outperformed baselines under our global evaluation score. Notably, the top entry exceeded the performance of the original OpenFOAM solver on aggregate metrics, illustrating the promise of ML-based surrogates to outperform traditional solvers under tailored criteria. Drawing from these results, we analyze the key design principles of top submissions, assess the robustness of our evaluation framework, and offer guidance for future scientific ML challenges.

Action Recognition with Deep Multiple Aggregation Networks

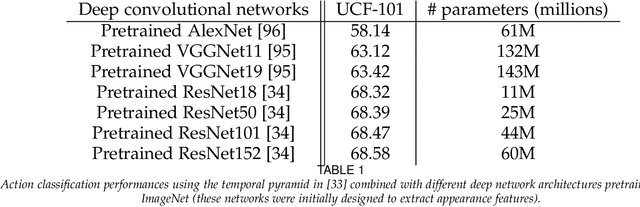
Most of the current action recognition algorithms are based on deep networks which stack multiple convolutional, pooling and fully connected layers. While convolutional and fully connected operations have been widely studied in the literature, the design of pooling operations that handle action recognition, with different sources of temporal granularity in action categories, has comparatively received less attention, and existing solutions rely mainly on max or averaging operations. The latter are clearly powerless to fully exhibit the actual temporal granularity of action categories and thereby constitute a bottleneck in classification performances. In this paper, we introduce a novel hierarchical pooling design that captures different levels of temporal granularity in action recognition. Our design principle is coarse-to-fine and achieved using a tree-structured network; as we traverse this network top-down, pooling operations are getting less invariant but timely more resolute and well localized. Learning the combination of operations in this network -- which best fits a given ground-truth -- is obtained by solving a constrained minimization problem whose solution corresponds to the distribution of weights that capture the contribution of each level (and thereby temporal granularity) in the global hierarchical pooling process. Besides being principled and well grounded, the proposed hierarchical pooling is also video-length and resolution agnostic. Extensive experiments conducted on the challenging UCF-101, HMDB-51 and JHMDB-21 databases corroborate all these statements.

Deep hierarchical pooling design for cross-granularity action recognition

In this paper, we introduce a novel hierarchical aggregation design that captures different levels of temporal granularity in action recognition. Our design principle is coarse-to-fine and achieved using a tree-structured network; as we traverse this network top-down, pooling operations are getting less invariant but timely more resolute and well localized. Learning the combination of operations in this network -- which best fits a given ground-truth -- is obtained by solving a constrained minimization problem whose solution corresponds to the distribution of weights that capture the contribution of each level (and thereby temporal granularity) in the global hierarchical pooling process. Besides being principled and well grounded, the proposed hierarchical pooling is also video-length agnostic and resilient to misalignments in actions. Extensive experiments conducted on the challenging UCF-101 database corroborate these statements.

Human Action Recognition with Multi-Laplacian Graph Convolutional Networks

Convolutional neural networks are nowadays witnessing a major success in different pattern recognition problems. These learning models were basically designed to handle vectorial data such as images but their extension to non-vectorial and semi-structured data (namely graphs with variable sizes, topology, etc.) remains a major challenge, though a few interesting solutions are currently emerging. In this paper, we introduce MLGCN; a novel spectral Multi-Laplacian Graph Convolutional Network. The main contribution of this method resides in a new design principle that learns graph-laplacians as convex combinations of other elementary laplacians each one dedicated to a particular topology of the input graphs. We also introduce a novel pooling operator, on graphs, that proceeds in two steps: context-dependent node expansion is achieved, followed by a global average pooling; the strength of this two-step process resides in its ability to preserve the discrimination power of nodes while achieving permutation invariance. Experiments conducted on SBU and UCF-101 datasets, show the validity of our method for the challenging task of action recognition.

Human Action Recognition with Deep Temporal Pyramids

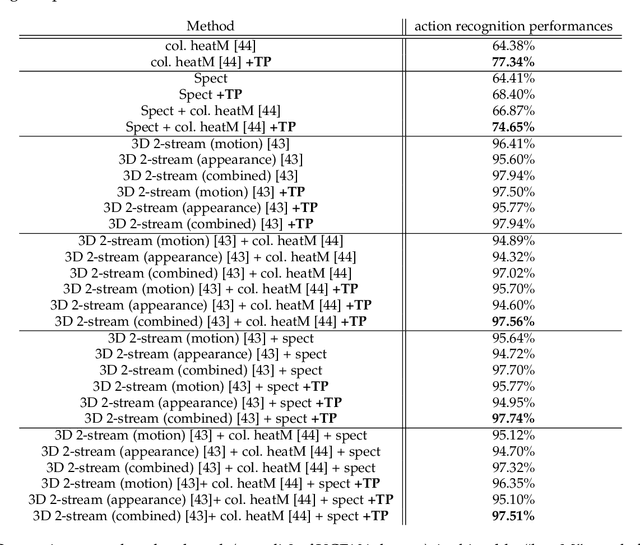
Deep convolutional neural networks (CNNs) are nowadays achieving significant leaps in different pattern recognition tasks including action recognition. Current CNNs are increasingly deeper, data-hungrier and this makes their success tributary of the abundance of labeled training data. CNNs also rely on max/average pooling which reduces dimensionality of output layers and hence attenuates their sensitivity to the availability of labeled data. However, this process may dilute the information of upstream convolutional layers and thereby affect the discrimination power of the trained representations, especially when the learned categories are fine-grained. In this paper, we introduce a novel hierarchical aggregation design, for final pooling, that controls granularity of the learned representations w.r.t the actual granularity of action categories. Our solution is based on a tree-structured temporal pyramid that aggregates outputs of CNNs at different levels. Top levels of this hierarchy are dedicated to coarse categories while deep levels are more suitable to fine-grained ones. The design of our temporal pyramid is based on solving a constrained minimization problem whose solution corresponds to the distribution of weights of different representations in the temporal pyramid. Experiments conducted using the challenging UCF101 database show the relevance of our hierarchical design w.r.t other related methods.