Deep Learning-based Auto-encoder for Time-offset Faster-than-Nyquist Downlink NOMA with Timing Errors and Imperfect CSI

In this paper, we examine the encoding and decoding of transmitted sequences for downlink time-offset with faster than Nyquist signaling NOMA (T-NOMA). As a baseline, we use the singular value decomposition (SVD)-based scheme proposed in previous studies for encoding and decoding. Even though this SVD-based scheme provides reliable communication, its time complexity increases quadratically with the sequence length. We propose a convolutional neural network (CNN) auto-encoder (AE) for encoding and decoding with linear time complexity. We explain the design of the encoder and decoder architectures and the training criteria. By examining several variants of the CNN AE, we show that it can achieve an excellent trade-off between performance and complexity. A proposed CNN AE outperforms the SVD method using a lower implementation complexity by approximately 2 dB in a T-NOMA system with two users assuming no timing offset errors or channel state information estimation errors. In the presence of channel state information (CSI) error variance of 1$\%$ and uniform timing error at $\pm$4\% of the symbol interval, the proposed CNN AE provides up to 10 dB SNR gain over the SVD method. We also propose a novel modified training objective function consisting of a linear combination of the traditionally used cross-entropy (CE) loss function and a closed-form expression for the bit error rate (BER) called the Q-loss function. Simulations show that the modified loss function achieves SNR gains of up to 1 dB over the CE loss function alone. Finally, we investigate several novel CNN architectures for both the encoder and decoder components of the AE that employ additional linear feed-forward connections between the CNN stages; experiments show that these architectural innovations achieve additional SNR gains of up to 2.2 dB over the standard serial CNN AE architecture.

Reduced Complexity Neural Network Equalizers for Two-dimensional Magnetic Recording

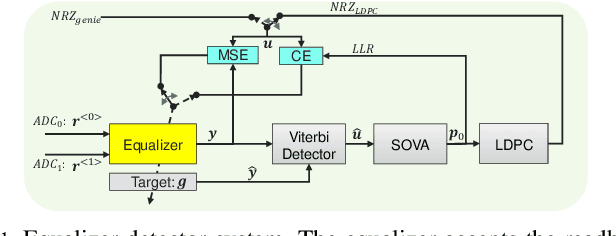
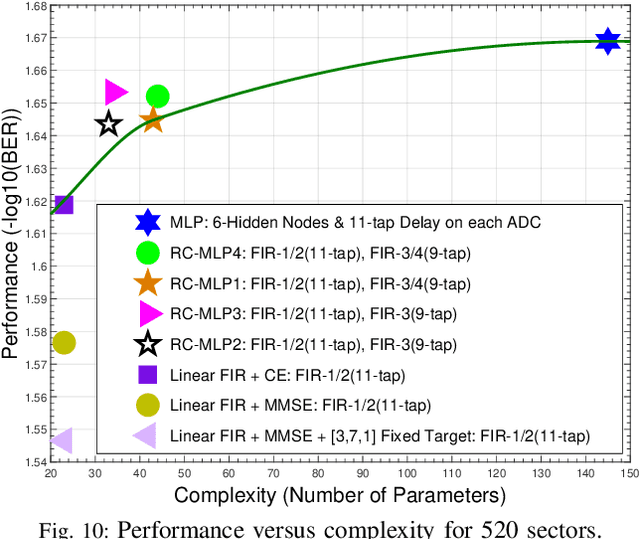
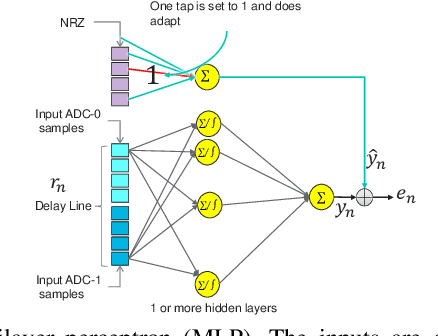
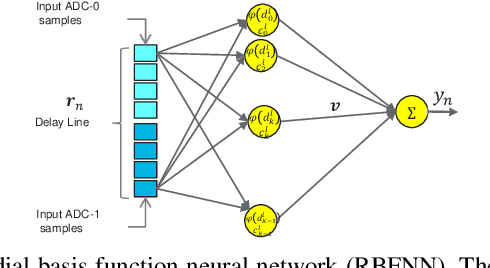
Recent studies show promising performance gains achieved by non-linear equalization using neural networks (NNs) over traditional linear equalization in two-dimensional magnetic recording (TDMR) channels. But the examined neural network architectures entail much higher implementation complexities compared with the linear equalizer, which precludes practical implementation. For example, among the low complexity reported architectures, the multilayer perceptron (MLP) requires about 6.6 times increase in complexity over the linear equalizer. This paper investigates candidate reduced complexity neural network architectures for equalization over TDMR. We test the performance on readback signals measured over an actual hard disk drive with TDMR technology. Four variants of a reduced complexity MLP (RC-MLP) architecture are proposed. A proposed variant achieves the best balance between performance and complexity. This architecture consists of finite-impulse response filters, a non-linear activation, and a hidden delay line. The complexity of the architecture is only 1.59 times the linear equalizer's complexity, while achieving most of the performance gains of the MLP.