Database Views as Explanations for Relational Deep Learning

In recent years, there has been significant progress in the development of deep learning models over relational databases, including architectures based on heterogeneous graph neural networks (hetero-GNNs) and heterogeneous graph transformers. In effect, such architectures state how the database records and links (e.g., foreign-key references) translate into a large, complex numerical expression, involving numerous learnable parameters. This complexity makes it hard to explain, in human-understandable terms, how a model uses the available data to arrive at a given prediction. We present a novel framework for explaining machine-learning models over relational databases, where explanations are view definitions that highlight focused parts of the database that mostly contribute to the model's prediction. We establish such global abductive explanations by adapting the classic notion of determinacy by Nash, Segoufin, and Vianu (2010). In addition to tuning the tradeoff between determinacy and conciseness, the framework allows controlling the level of granularity by adopting different fragments of view definitions, such as ones highlighting whole columns, foreign keys between tables, relevant groups of tuples, and so on. We investigate the realization of the framework in the case of hetero-GNNs. We develop heuristic algorithms that avoid the exhaustive search over the space of all databases. We propose techniques that are model-agnostic, and others that are tailored to hetero-GNNs via the notion of learnable masking. Our approach is evaluated through an extensive empirical study on the RelBench collection, covering a variety of domains and different record-level tasks. The results demonstrate the usefulness of the proposed explanations, as well as the efficiency of their generation.

Towards Unbiased Exploration in Partial Label Learning

We consider learning a probabilistic classifier from partially-labelled supervision (inputs denoted with multiple possibilities) using standard neural architectures with a softmax as the final layer. We identify a bias phenomenon that can arise from the softmax layer in even simple architectures that prevents proper exploration of alternative options, making the dynamics of gradient descent overly sensitive to initialisation. We introduce a novel loss function that allows for unbiased exploration within the space of alternative outputs. We give a theoretical justification for our loss function, and provide an extensive evaluation of its impact on synthetic data, on standard partially labelled benchmarks and on a contributed novel benchmark related to an existing rule learning challenge.

Solving Inverse Problems for Spectral Energy Distributions with Deep Generative Networks

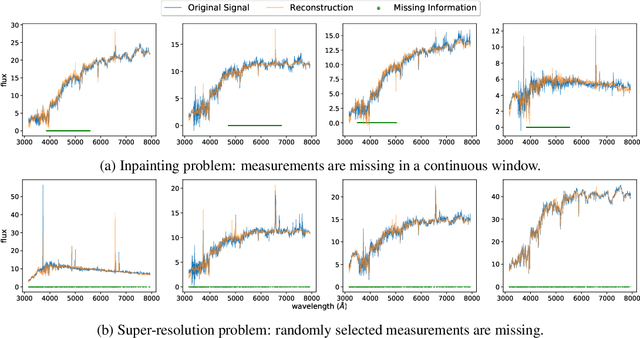
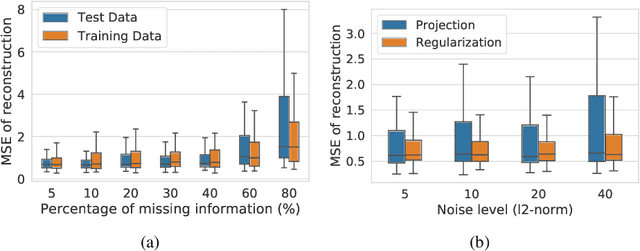
We propose an end-to-end approach for solving inverse problems for a class of complex astronomical signals, namely Spectral Energy Distributions (SEDs). Our goal is to reconstruct such signals from scarce and/or unreliable measurements. We achieve that by leveraging a learned structural prior in the form of a Deep Generative Network. Similar methods have been tested almost exclusively for images which display useful properties (e.g., locality, periodicity) that are implicitly exploited. However, SEDs lack such properties which make the problem more challenging. We manage to successfully extend the methods to SEDs using a Generative Latent Optimization model trained with significantly fewer and corrupted data.