Node Splitting: A Scheme for Generating Upper Bounds in Bayesian Networks

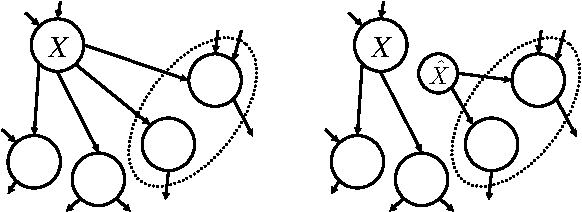
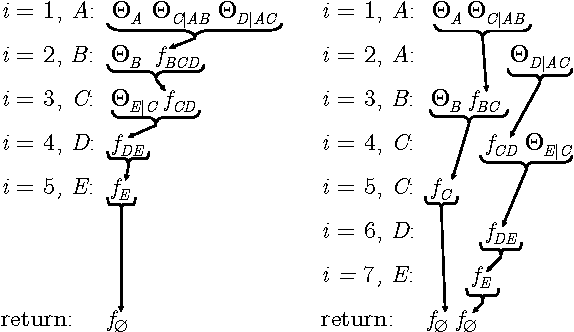
We formulate in this paper the mini-bucket algorithm for approximate inference in terms of exact inference on an approximate model produced by splitting nodes in a Bayesian network. The new formulation leads to a number of theoretical and practical implications. First, we show that branchand- bound search algorithms that use minibucket bounds may operate in a drastically reduced search space. Second, we show that the proposed formulation inspires new minibucket heuristics and allows us to analyze existing heuristics from a new perspective. Finally, we show that this new formulation allows mini-bucket approximations to benefit from recent advances in exact inference, allowing one to significantly increase the reach of these approximations.

Approximating the Partition Function by Deleting and then Correcting for Model Edges

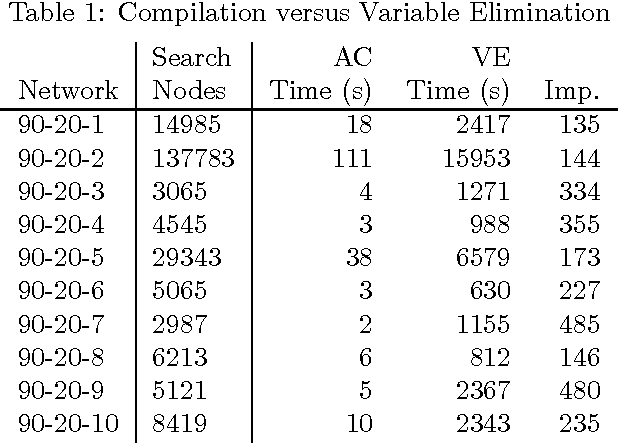
We propose an approach for approximating the partition function which is based on two steps: (1) computing the partition function of a simplified model which is obtained by deleting model edges, and (2) rectifying the result by applying an edge-by-edge correction. The approach leads to an intuitive framework in which one can trade-off the quality of an approximation with the complexity of computing it. It also includes the Bethe free energy approximation as a degenerate case. We develop the approach theoretically in this paper and provide a number of empirical results that reveal its practical utility.

EDML: A Method for Learning Parameters in Bayesian Networks

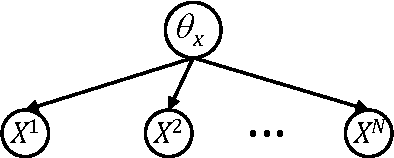
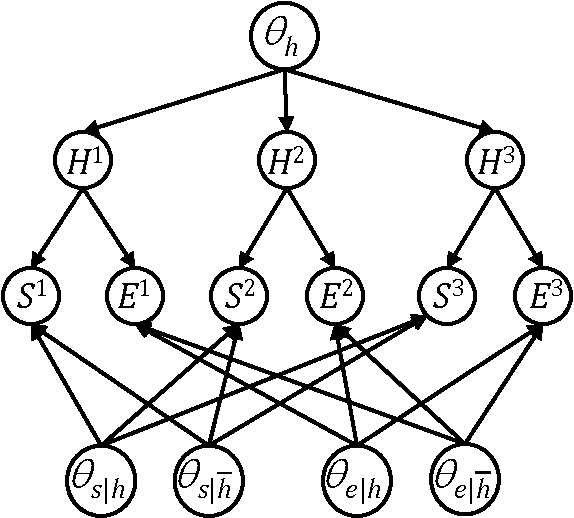
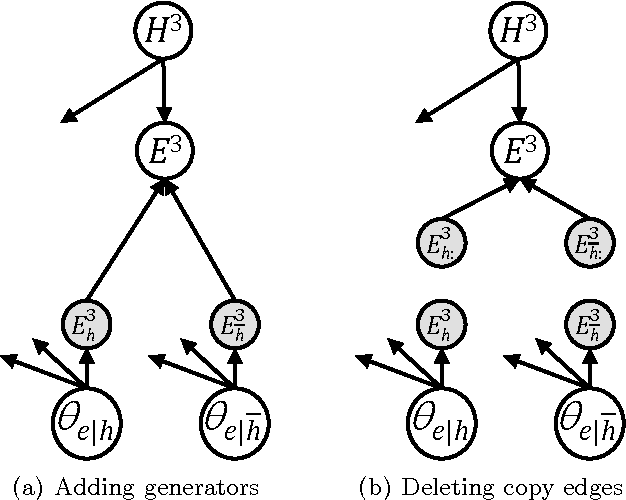
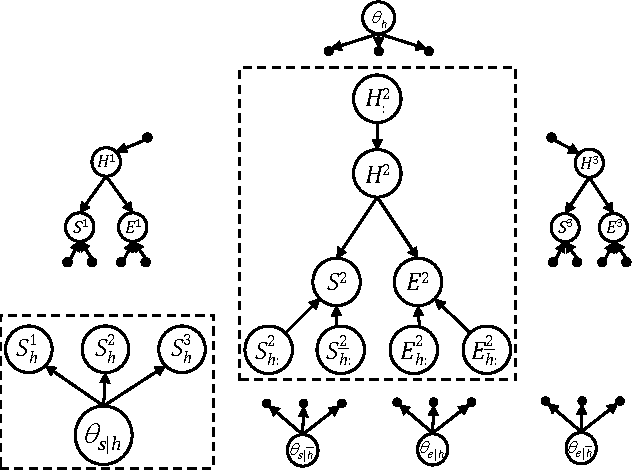
We propose a method called EDML for learning MAP parameters in binary Bayesian networks under incomplete data. The method assumes Beta priors and can be used to learn maximum likelihood parameters when the priors are uninformative. EDML exhibits interesting behaviors, especially when compared to EM. We introduce EDML, explain its origin, and study some of its properties both analytically and empirically.

Compilation of Propositional Weighted Bases

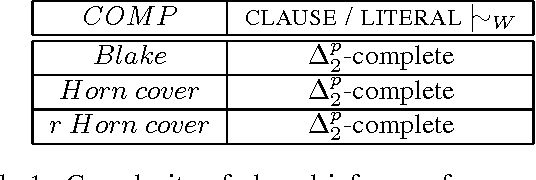
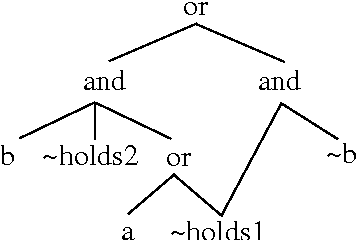
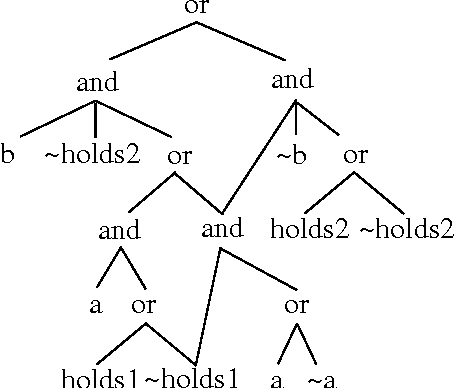
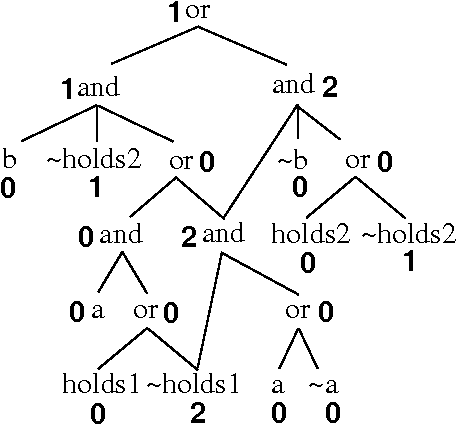
In this paper, we investigate the extent to which knowledge compilation can be used to improve inference from propositional weighted bases. We present a general notion of compilation of a weighted base that is parametrized by any equivalence--preserving compilation function. Both negative and positive results are presented. On the one hand, complexity results are identified, showing that the inference problem from a compiled weighted base is as difficult as in the general case, when the prime implicates, Horn cover or renamable Horn cover classes are targeted. On the other hand, we show that the inference problem becomes tractable whenever DNNF-compilations are used and clausal queries are considered. Moreover, we show that the set of all preferred models of a DNNF-compilation of a weighted base can be computed in time polynomial in the output size. Finally, we sketch how our results can be used in model-based diagnosis in order to compute the most probable diagnoses of a system.

On the tractable counting of theory models and its application to belief revision and truth maintenance

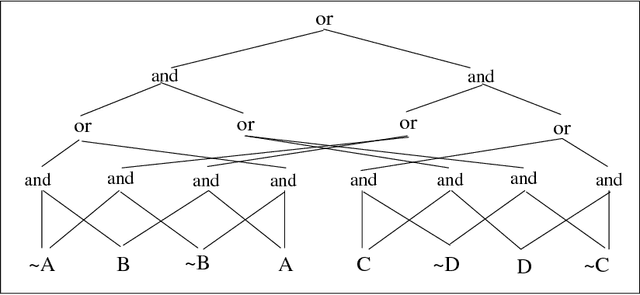
We introduced decomposable negation normal form (DNNF) recently as a tractable form of propositional theories, and provided a number of powerful logical operations that can be performed on it in polynomial time. We also presented an algorithm for compiling any conjunctive normal form (CNF) into DNNF and provided a structure-based guarantee on its space and time complexity. We present in this paper a linear-time algorithm for converting an ordered binary decision diagram (OBDD) representation of a propositional theory into an equivalent DNNF, showing that DNNFs scale as well as OBDDs. We also identify a subclass of DNNF which we call deterministic DNNF, d-DNNF, and show that the previous complexity guarantees on compiling DNNF continue to hold for this stricter subclass, which has stronger properties. In particular, we present a new operation on d-DNNF which allows us to count its models under the assertion, retraction and flipping of every literal by traversing the d-DNNF twice. That is, after such traversal, we can test in constant-time: the entailment of any literal by the d-DNNF, and the consistency of the d-DNNF under the retraction or flipping of any literal. We demonstrate the significance of these new operations by showing how they allow us to implement linear-time, complete truth maintenance systems and linear-time, complete belief revision systems for two important classes of propositional theories.